Prev Page--Site 10 || Next Page--Appendices
Transport modeling
Solute transport during steady-state flow in homogeneous soils is described in this study by the one-dimensional deterministic convection-dispersion equation for a single solute:
![]()
where C is the solute concentration in the liquid phase [M/L3], s is the adsorbed mass concentration per unit mass of the solid phase [M/M], D is the dispersion coefficient reflecting the combined effects of diffusion and hydrodynamic dispersion on transport [L 2T], ρb is the soil bulk density [M/L3], Θ is the volumetric water content [L3/L3], V = q/Θ is the pore water velocity [L/T] (where q is the hydraulic flux density and Θ is the volumetric water content), x is the distance [L], t is time [T], and μ is the degradation coefficient [T-1], which is assumed to be a rate constant for first-order decay. Equilibrium adsorbed and solute concentrations are related by an assumed linear or linearized isotherm of the form
![]()
where k is an empirical distribution constant [L3/M], often referred to as the distribution coefficient Kd.
Assuming that local equilibrium conditions exist, substitution of Eq. (2) into Eq. (1) yields
![]()
in which the retardation factor R, which accounts for chemical interaction between the chemical and the porous medium, is given by
![]()
For a mobile, nonreactive chemical, such as bromide, R = 1 and µ = 0, and Eq. (3) reduces to
![]()
Equations (3) and (5) are solved subject to a uniform initial concentration Ci, a pulse-type boundary condition at the soil surface, and a semi-infinite (0 ≤ x < ∞) bottom boundary condition:
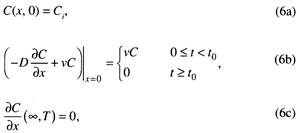
where C0 is the input concentration and t0 is the solute pulse duration.
Cassel et al. (1975) and Wierenga (1977) have found that, by using mean values for Darcian flux and profile water content, the steady-state solution to the convection-dispersion Eq. (5) gives a good approximation of solute transport data obtained under transient conditions. Thus, even under transient flow conditions, the assumption of an equivalent uniform water flux and water content may be adequate for employing Eqs. (3) and (5).
The analytical solution for this problem is given by van Genuchten and Alves (1982) and by Parker and van Genuchten (1984a) for both volume-averaged resident concentrations of the solute in the liquid phase and flux-averaged concentrations. Volume-averaged concentration refers to the mass of solute per unit volume of fluid contained in an elementary volume of the system at a given instant. Flux-averaged concentration refers to the mass of solute per unit volume of fluid passing through a given cross section at an elementary time interval (Kreft and Zuber, 1978), that is, the ratio of the solute flux to the volumetric fluid flux. We used the least-squares regression method described by Parker and van Genuchten (1984a) to fit the curves of the analytical solution of Eqs. (3), (5), and (6) to the observed data for the suction lysimeters and the 1-in. (2.5-cm) diameter cores collected at different times during the experiment. To optimize the unknown (or partially known) parameters v, D, R, m, and to in Eqs. (3) and (6) from observed temporal and spatial concentration data, we used the Parker and van Genuchten (1984a) CXTFIT program. One restriction is that v and R cannot be optimized simultaneously because of similar effects on the effective transport rate vIR in the soil profile. For bromide, R was taken to be unity with no adsorption.
Parker and van Genuchten (1984b) showed that there is a significant difference in calculated parameter values that depends on whether a volume- or a flux-averaged concentration is used. However, for small values of the dimensionless group (vx/D), differences between the two concentration modes should be small. In our case relatively small differences in the bromide fitted parameters were observed when flux or resident concentrations were employed in the parameter-optimization program.
Although the convection-dispersion transport equation is the foundation on which numerous mathematical analyses of solute transport in porous media have been based, questions have been raised recently regarding the applicability of this model to media exhibiting large variations in pore-water velocities (caused by the presence of continuous large pores) or by field-scale variability in hydraulic properties (van Genuchten and Wierenga, 1976; Parker and van Genuchten, 1984b). Nielsen et al. (1986) list other difficulties associated with the use of Eq. (3) or (5). In using the convection-dispersion model [Eq. (3) or (5)], one generally assumes that chemical and physical equilibrium exists between the displacing solution and the original soil solution. Unfortunately, it appears that for many soils such an equilibrium does not exist, resulting in partial displacement of the soil solution by the invading solution (Wierenga, 1982, 1987). One partly successful approach to describing solute movement through soils with partial displacement is to divide soil water into mobile and immobile, or stagnant (not in equilibrium with the infiltrating water), zones (van Genuchten and Wierenga, 1976). Convection-dispersion transport is confined to the mobile water phase, and solute movement into and out of the immobile water is assumed to be a relatively slow diffusion-controlled process; these combined processes result in early breakthrough and tailing of solute distribution curves. Under certain conditions, such as low apparent dispersivity, all solutions of the classical convection-dispersion model yield symmetric concentration distributions in time and space. Experiments on fractured or aggregate media, however, yield asymmetric spatial and temporal concentration distributions with first moments significantly different from those anticipated for symmetric distributions [e.g., Bouma and Wösten (1979)]. Such discrepancies are often regarded as incongruous with the classical convection-dispersion equation (Parker and van Genuchten, 1984b), a view corroborated by our field results.
As a result of the discrepancies of the convection-dispersion equation vis-à-vis the field results, breakthrough curves for bromide and atrazine could not be successfully simulated with the Parker and van Genuchten (1984a) models, including the two-site-two-region (mobile-immobile zones) nonequilibrium model. The problem was further compounded by the observed large variability of soil core sampling at random points within the relatively small flooded area of both sites. However, we encountered relatively better results when simulating the vertical profiles of bromide sampled from suction lysimeters at different times. The observed exponential decay of concentration-depth distributions generally fits the expected classical patterns better than concentration-time breakthrough curves. Table 3 presents two results of bromide fitted model parameters v, D, and t0, assuming R = 1. The two sampling dates used in the table had the most complete suction lysimeter data. Although the chemical solution at both sites was applied for approximately one day at the surface, our shallowest suction lysimeter was at a depth of 15 cm (0.5 ft). Thus the exact duration of the applied pulse relative to the sampling port location is somewhat ambiguous, and the pulse duration was treated as an unknown parameter in this study.
Table 3--Fitted model parameters for bromide collected from suction lysimeters.
| Site | Sampling date |
v (cm/d) ± std. error |
D (cm2/d) ± std. error |
t0 (day) ± std. error |
R2 | Number of samples |
|---|---|---|---|---|---|---|
| 6 | Sept. 18, 1987 | 13.52 ± 0.17 | 19.20 ± 1.82 | 2.43 ± 0.03 | 0.9998 | 6 |
| 7 | Oct. 8, 1987 | 15.65 ± 1.12 | 19.76 ± 8.29 | 1.61 ± 0.00 | 0.9875 | 7 |
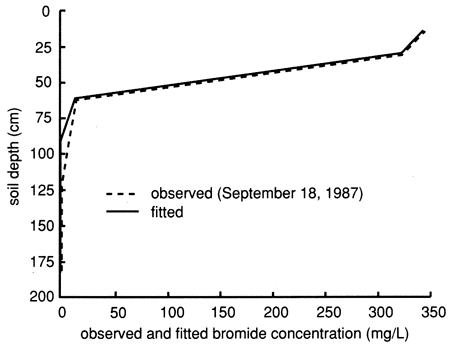
Although the estimated average pore-water velocity overestimated the average measured pore-water velocity for site 6 and underestimated the one for site 7, as determined from the instantaneous profile method (see figs. 13, 18, 43, and 45), the estimated velocity values are of the correct order of magnitude. Figure 60 depicts the simulated and measured site 6 bromide data for bromide versus depth for September 18, 1987, three days after the chemical solution was applied at the site.
Figure 60--Observed (dashed line) and fitted (solid line) flux-averaged bromide concentrations with depth for site 6. The observed data were taken on September 18, 1987.
Conclusions and recommendations
We find the combined use of flooding experiments for simultaneously studying both the chemical and physical flow characteristics of the study sites a powerful field technique. Although we observed relatively high nitrate concentrations in both the vadose and the aquifer zone in one of our study sites (site 7), atrazine was not detected in either the deeper vadose zone or the underlying aquifer in any of the study sites. We also have no evidence of atrazine accumulation on top of clay layers, despite repeated soil core sampling before, during, and after the chemical flooding experiments. [Clay layers sampled during trench excavation on August 4-6, 1987, from cropland sites in Pawnee County (sec. 14, T. 23 S., R. 15 W., Carwile soil; samples for atrazine analysis taken from 38-52 cm, 52-92 cm, and 111-123 cm [1.2-1.7 ft, 1.7-3.0 ft, and 3.6-4.0 ft]), Edwards County (sec. 5, T. 24 S., R. 16 W., Naron soil; samples for atrazine analysis taken from 43-68 cm, 68-91 cm, and 146-161 cm [1.4-2.2 ft, 2.2-3.0 ft, and 4.8-5.3 ft]), Pratt County (site 7; samples for atrazine analysis taken from 32-50 cm, 135-157 cm, and 157-167 cm [1.0-1.6 ft, 4.4-5.2 ft, and 5.2-5.5 ft]), and Stafford County (site 6; samples for atrazine analysis taken from 48-66 cm and 66-77 cm [1.6-2.2 ft and 2.2-2.5 ft]) revealed no detectable atrazine at a detection limit of 0.04 mg/kg.] The evidence, albeit from limited sampling (because of financial constraints), that atrazine readily breaks down to hydroxyatrazine, even if soil pH is not low and even if clay and organic matter content are relatively low, may explain the observed atrazine distribution. Atrazine degradation follows approximately first-order kinetics with a half-life of approximately two weeks. We also have evidence of biodegradation by-products, indicating that both biologic and chemical degradation occur in the soil profile. Based on the results of this study, the probability that atrazine will leach through the soils to the underlying aquifer in the Great Bend Prairie under present conditions seems remote.
The nitrate data from the suction lysimeters at site 7 indicate a close relationship between irrigation and nitrate movement into the subsurface; that is, nitrate is moving into the deeper soil profile and into the ground water as a consequence of irrigation. However, low nitrate levels in both the soil and the ground water were observed at site 6. Comparison of the total dissolved solids content in the ground water from sites 6, 7, and 10 demonstrates the impact of continuous irrigation on the general ground-water quality at sites 6 and 7, which exhibit much higher total dissolved solids contents than the nonirrigated site 10.
Chemical transport analysis at sites 6 and 7 indicates that the classical processes of chemical movement based on equilibrium conditions and diffuse flow through porous media are not appropriate for either site. The persistence of bromide in the upper soil horizons indicates that the applied solution displaced the existing soil pore water during percolation at site 6, which was already at or near saturation when the bromide-tagged solution was applied. Thus we have evidence of slug flow or lack of complete mixing between invading and in situ solutions. Some preferential flow was also observed, although to a lesser extent than slug flow. As a result of slug movement, piston-type displacement of more-saline soil solutions in the soil profile to the water table occurred. The significance of such observations from site 6 to agricultural chemical movement is that, during periods of unusually high rainfall and ponding in the area or during excessive flood irrigation, downward movement of chemicals concentrated in soils might be triggered, affecting the quality of shallow ground water.
In contrast to what was observed at site 6, slug displacement at site 7 was subdued, and channelization or preferential flow of percolating soil water, with little of the initial soil solution being displaced, predominated. The importance of the results to agricultural chemical movement is that dissolved chemicals can bypass certain soil zones and move to greater depths than expected. When water becomes channelized in field soil, only a small percentage of the total matrix is involved in the flow process. Thus movement of chemicals in field soils occurs through a combination of displacement of native fluids (slug movement) and bypassing of native fluids by preferential flow. Therefore the assumption of diffuse flow through porous media under physical and chemical equilibrium between invading and native solutions-a standard assumption in mathematical formulations of contaminant transport-is not supported by our field study. Therefore concentrated efforts to quantify preferential and incompletely mixed flow situations are urgently needed.
As a result of our sampling experience, we offer the following recommendations.
- Collect multiple samples per depth over a small area of interest, and use the average concentration per depth for analysis.
- Sample the entire depth of interest in one continuous core. The 30-cm (1-ft) depth intervals we used with a hand core sampler occasionally created cavings at each depth increment, thus altering the soil profile distribution of the chemical of interest.
- Do not rely entirely on suction lysimeters because (a) they may fail; (b) leakage along the side walls of the lysimeter cannot be verified and quantified; (c) they do not work under freezing conditions; (d) even if they do work, one may not obtain a sample because of soil dryness; and (e) the obtained samples may not represent true soil conditions because vacuum application dries up the area in the immediate vicinity of the porous cup and thus soil-water flow may preferentially diverge from the porous cup vicinity. In addition, because of the continuously varying vacuum conditions in the suction lysimeters, different pore fractions are sampled at different times. Therefore we recommend using both soil cores and suction lysimeters (preferably maintained at constant vacuum) for chemical sampling.
- Chemical analyses should be conducted as early as possible after sampling so that problems can be addressed effectively and sampling redone, if necessary. It is essential that sequential or time-series sampling be guided continuously by the chemical analysis results to provide maximum flexibility. Sending samples to outside laboratories and waiting for months to receive results defeats the purpose of any serious study.
In addition to these four recommendations, we outline the following research items for further study:
- A laboratory study of atrazine degradation processes using running pairs of soil columns, one of which is sterilized (either chemically or by autoclaving), so that microbial decomposition of atrazine can be ascertained. These column pairs should be run under different wetness conditions.
- Monitoring of the present sites and additional sites with regard to additional pesticides and nitrate, with particular emphasis on environmental and land-use effects. Given the high nitrate concentrations observed at site 7, a more detailed and regional study of the nitrate problem in the Great Bend Prairie is needed.
- An evaluation of numerical simulation approaches to agrichemical movement with particular emphasis on preferential flow and incomplete mixing processes.
Prev Page--Site 10 || Next Page--Appendices
Kansas Geological Survey, Geohydrology
Placed on web Aug. 23, 2010; originally published 1990.
Comments to webadmin@kgs.ku.edu
The URL for this page is http://www.kgs.ku.edu/Publications/Bulletins/GW12/07_conc.html