Prev Page--Digital Simulation || Next Page--Management Options
Parameter Estimation or Model Calibration
Introduction
Before an appropriate model can be used as a predictive or problem-solving device for the area of interest, it must be "calibrated" by using data from the physical system to be simulated. The two primary objectives of calibration are 1) to adjust the model's input data (such as aquifer properties, sources and sinks, boundary, and initial conditions) to best approximate the physical system and screen erroneous data; and 2) to determine the sensitivity of the model to the input variables (Huntoon, 1974). In practice, the calibration of a ground- water model is frequently accomplished through a trial-and-error adjustment of the model's input data to modify the model's output. Because a large number of related factors affect the output, this may become a highly subjective procedure. Recent advances in parameter estimation procedures (Seinfeld and Lapidus, 1974) help eliminate some of the subjectivity in model calibration.
The application of a computer model requires that certain terms be known for each node. These include the elevation of the base of the aquifer, initial water-table elevation, net withdrawal values, hydraulic conductivity, and storativity. Elevation of aquifer base and initial water-table may be obtained using physical measurements for each node. The values of hydraulic conductivity and storativity as well as net withdrawal values are much harder to determine. Many methods have been developed to determine values for the aquifer parameters but most of these provide estimates for only a relatively small area.
Parameter estimation procedures provide a tool for determining aquifer parameters for a set of points in an aquifer by treating initial estimates of those parameters as terms to be adjusted on the basis of some criterion of "goodness of fit." The key point in the adjustment of parameters is the determination of the computer-model sensitivity to changes of the parameters. The sensitivity is indicated by the extent the simulated water levels react to a change in an aquifer parameter. A change in the simulated water level will occur not only for the node at which the change in the parameter occurred, but also for the water level of the surrounding nodes. A change in a parameter for any one node will affect the head of all other nodes in the system.
Parameter Adjustment Procedure
The procedure used for adjusting the aquifer parameters is the method of steepest descent, also known as the method of gradients (Knowles and others, 1972). This procedure obtains the minimum of a function by determining the changes of the independent parameters that will result in the greatest rate of reduction of the function. The function to be minimized is the difference between the simulated and measured water levels. The independent parameters are the hydraulic conductivity, storativity and net withdrawal rates or fluxes.
The parameter adjustment procedure is as follows. First, the water levels for the year or years during which measured water levels are available are simulated. The measured water levels are used as starting points for each year's simulation, and the original estimates of hydraulic conductivity, storativity, and net withdrawal rates are used for each node. Second, the values of the coefficients and constants for all the sensitivity equations are determined. The sensitivity of any node's simulated water level with respect to one of the parameters may be expressed by the partial derivative expression of water level with respect to the parameter of interest. For further details on the derivation and application of the equations involved in such sensitivity analysis, see Knowles and others (1972).
Third, the aquifer parameters are adjusted according to the steepest descent algorithm (Vemuri and Karplus, 1969)
φm+1 = φm - λ(δH/δφ)
where φ is an aquifer parameter (hydraulic conductivity, storativity or net withdrawal value)
δH/δφ is the sensitivity of the water level with respect to parameter φ
λ is a scalar such that λ>O
and m is an iteration index.
The order of nodal adjustment was based on the decreasing size of the simulation error, that is, the difference between the simulated water-table elevation and the measured water-table elevation. The node with the largest simulation error was adjusted first, the node with the second largest error was adjusted second, and so on. The adjustment procedure was terminated when the simulation error of any node was less than 0.5 foot. This termination criterion reduced the execution time of the computer program; also, a simulation error of that size was not considered significant.
Once a node was chosen for adjustment, the sensitivities based on a specified number of nodes surrounding the chosen node were calculated. Although a change of a parameter for any node will theoretically affect the simulated water level for all other nodes in the system, the effect on distant nodes will be slight. This fact suggests that acceptable results could be obtained by a procedure that differentiates only the equations of the nodes most affected by a change at node i,j. Knowles and others (1972) tried several arrangements involving 48, 24, and 12 nodes surrounding node i,j, which were within three or two tiers of that node. They found that the 12 node arrangement surrounding the node of interest i,j (Fig. 28) was not only much more economical to solve but also accurate enough, as the values of the partial derivatives for the nodes in the corners of the region were very small, resulting in a very small change in the simulated head value.
Figure 28--12-node arrangement surrounding the central node i,j used in calculating the sensitivities of a node.
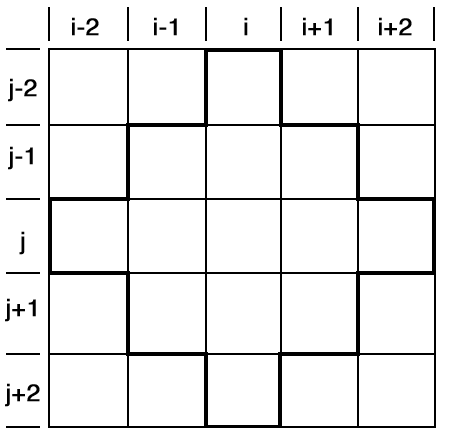
After the parameters had been adjusted, the simulation errors for the twelve adjoining nodes were changed to reflect the expected change in the simulated water level for the center node. The water levels for the surrounding nodes will also change since they are functions of the water level of the adjusted node. The procedure was then repeated, beginning with the simulation of new water levels, until the simulated errors were so small that additional iterations were not justified.
Implementation of the Parameter Adjustment Procedure
The water-table configuration served as the basis for evaluating goodness of fit with respect to adjustments of hydraulic conductivity, storativity, and boundary fluxes. Initial estimates of these parameters were used in the calibration of the model. These were adjusted between successive simulations with the objective of minimizing the differences between observed and computed water-table elevations in the study area. In order to avoid the uncertainties related to the amount of net pumpage in calibrating the model, water-level measurements taken during the 1945-47 period were used. It is assumed that the water-table configuration then was closer to equilibrium conditions than it is today and that whatever groundwater was pumped out of the aquifer was approximately replenished by natural recharge. Therefore, starting with that initial water-table surface, the present model was employed to calculate which distribution of aquifer parameters and boundary fluxes would keep that surface nearly constant. By minimizing the simulation errors, this procedure resulted in the distribution of aquifer parameters referred to below. It should be noted that if the pumpage distribution and water levels for several years had been available in adequate detail, this calibration procedure would have been more effective because data of several years would have been averaged, resulting in a better approximation of the aquifer parameters.
The parameters for all nodes were adjusted by the steepest descent procedure mentioned previously, using constraints on storativity, hydraulic conductivity, and fluxes. The two constraints applicable to the storativity were minimum and maximum allowable values of 0.05 and 0.25. The allowable limits for hydraulic conductivity were 0.03 and 14.0 acre-feet per square foot per year, which correspond approximately to the range from 25 to almost 12,500 gallons per day per square foot. The maximum change allowed in boundary fluxes was one acre-foot per acre per year, which, for a 3xl square mile area, represents 1,920 acre-feet per year. All the above figures are based on the types of sediments in Pawnee Valley and reflect the great variability of rocks in that Valley.
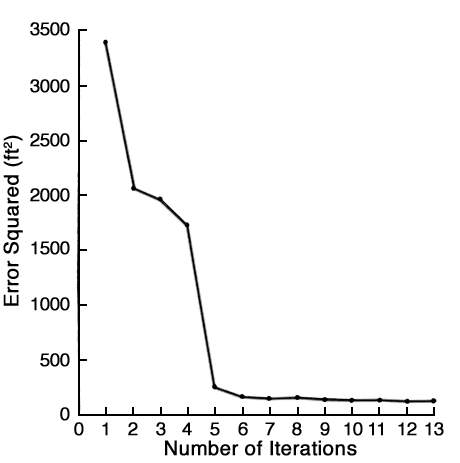
Table 14 shows the results of the parameter adjustment on the simulation errors for the 1945-47 calibration period. Figure 29 gives a graphical representation of the reduction of the simulation errors by using the adjusted values. As shown in Figure 30, the sum of the errors squared between observed and calculated water levels decreased as successive simulation tests were made. This figure indicates that the parameter adjustment procedure effectively reduced the magnitude of the error. After about ten tests, additional adjustments produced only very small improvements in the fit between observed and computed water levels.
Table 14--Comparison of Frequency of Errors During Parameter Adjustment for 1945-47.
| Range of Errors | Original Values |
After Two Iterations |
After Four Iterations |
Final Values (After 11 Iterations) |
|---|---|---|---|---|
| >16.5 | 1 | 1 | 0 | 0 |
| -16.5 to -13.5 | 0 | 0 | 0 | 0 |
| -13.5 to -10.5 | 2 | 0 | 0 | 0 |
| -10.5 to -7.5 | 5 | 0 | 0 | 0 |
| -7.5 to -4.5 | 1-2 | 3 | 0 | 0 |
| -4.5 to -1.5 | 23 | 10 | 6 | 0 |
| -1.5 to 1.5 | 18 | 79 | 99 | 107 |
| 1.5 to 4.5 | 26 | 13 | 4 | 3 |
| 4.5 to 7.5 | 16 | 1 | 1 | 0 |
| 7.5 to 10.5 | 5 | 3 | 0 | 0 |
| 10.5 to 13.5 | 3 | 1 | 1 | 1 |
| Sum of Error Squared (ft2) |
3,380 | 1,976 | 257 | 161 |
| Reduction of original Error Squared |
42% | 92% | 95% |
Figure 29--Histogram for the 1945-47 simulation errors
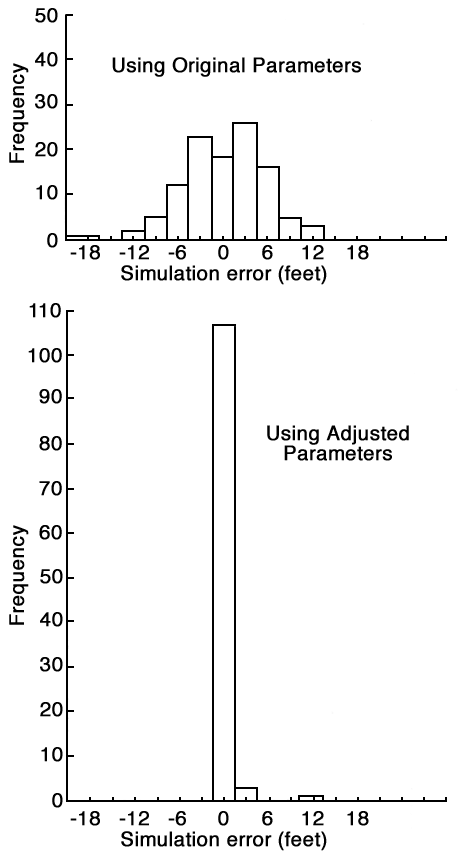
Figure 30--Plot of sum of error squared versus number of iterations.
If water-level data are available for N years, each year will result in a new set of parameters. These parameters are therefore N approximations to the actual values of the parameters, and the averages of the N values obtained are assumed to provide good estimates of their true value at each node. To reflect the continuity in space of the parameters, the values of hydraulic conductivity and storativity obtained at each node by this method were averaged with the corresponding values at surrounding nodes. Referring to Figure 28, the values of the average parameter, φ, were determined by the following formula:
φi,j = 1/16 (φi-1,j-1 + 2φi,j-1 + φi+1,j-1 + 2φi-1,j + 4φi,j + 2φi+1,j + φi-1,j+1 + 2φi,j+1 + φi+1,j+1)
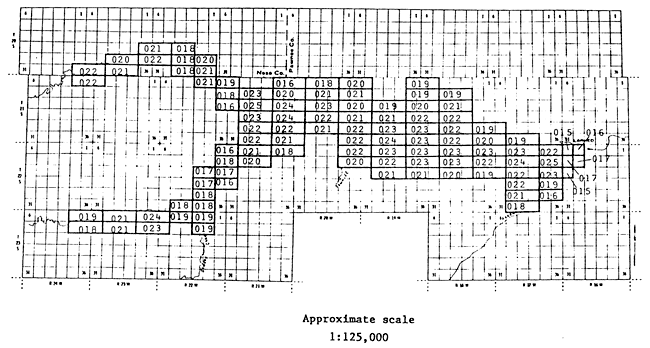
The resulting distributions of the average hydraulic conductivity and storativity are shown in Figures 31 and 32 respectively.
Figure 31--Distribution of Average hydraulic conductivity (aft/ft2/yr) based on parameter adjustment (last two digits are decimals, i.e., 131 = 1.31).
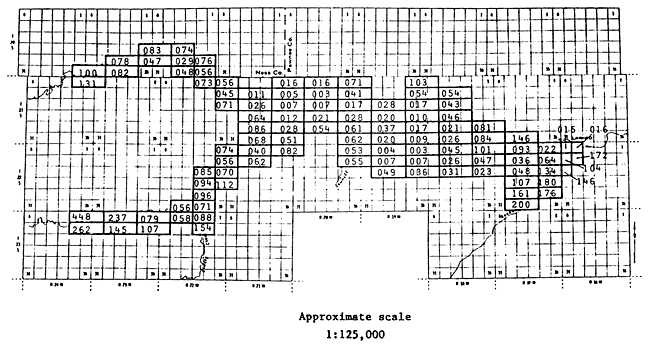
Figure 32--Distribution of Average Specific Yield (Sy) based on parameter adjustment (last two digits are decimals, i.e., 131 = 1.31).
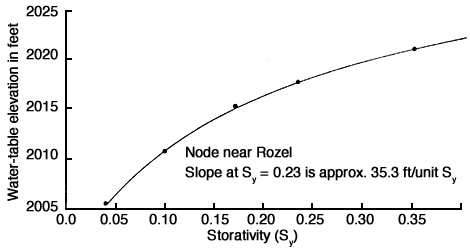
Another objective of the calibration procedure is to determine the sensitivity of the model to factors that affect groundwater flow. Evaluating the importance of each factor helps determine which data must be defined more accurately and which data are already adequate or require only minimal definition. If additional data cannot be collected, then the sensitivity tests can help to assess the reliability of the model by demonstrating the effect of a given range of uncertainty or error in the input data on the output of the model. The relative sensitivities of the parameters that affect flow will vary from problem to problem. Figures 33, 34, and 35 show the effects of changes of hydraulic conductivity, storativity, and fluxes on the simulated water levels at a randomly selected node at column 12, row 9 of the nodal grid system near Rozel (Fig. 26). From these figures it is concluded that the computed head is more sensitive to values of storativity and fluxes (both vertical and lateral) than to hydraulic conductivity values. The high sensitivity of computed hydraulic head to storativity is important because this property is the least well known at a given point in space and time. While the sensitivity of hydraulic head to fluxes is constant (linear), the sensitivity to hydraulic conductivity decreases with increasing hydraulic conductivity (Figs. 34 and 33).
Figure 33--Effect of changes in hydraulic conductivity on simulated water level of a node.
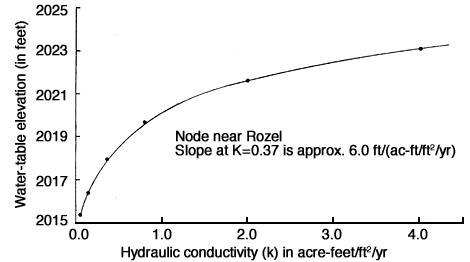
Figure 34--Effect of changes in net pumpage on simulated water level of a node.
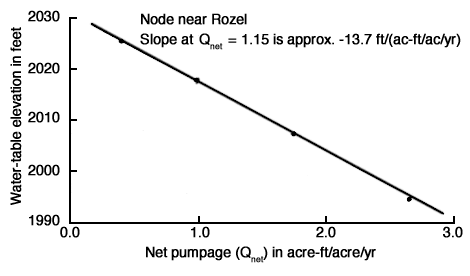
Figure 35--Effect of changes in storativity on simulated water level of a node.
Prev Page--Digital Simulation || Next Page--Management Options
Kansas Geological Survey, Hydrogeology
Placed on web Aug. 1, 2012; originally published April 1980.
Comments to webadmin@kgs.ku.edu
The URL for this page is http://www.kgs.ku.edu/Hydro/Publications/OFR80_6/06_calibrate.html