PfEFFER Concepts Models for Shaly Sandstones

Log Analysis Models for Shaly Sandstones

Shales have moderately low resistivities, as can be seen on any resistivity log, and their presence as a component of shaly sandstones introduces a conductivity contribution that should be included together with the conductivity of the pore formation water in detailed reservoir analysis. As a general statement, if uncorrected resistivities are used in a conventional clean reservoir calculation of a shaly sand zone, the result will be an overestimation of water saturation, since the resistivities have been reduced below their true values by the conductivity of the shale component.

Two model families of shaly sandstone equations have been developed as expansions of the Archie equation to accommodate the conductivity effects of clay minerals and compute more accurate water saturations (Worthington, 1985). The older model considered the shale as a homogeneous conductive medium and developed resistivity equations keyed to Vsh, the volumetric fraction of shale in the rock. Although the physical basis of the model is incorrect, the equations often provide reasonable approximate solutions to water saturation, especially when the equation parameters are adjusted so that the results conform with local water saturation data measured from cores or production tests. Some of these equations are still widely used for this reason and also because of their relative simplicity and limited demands on additional input parameters. One of the most commonly used equations of this type is the "Simandoux equation", introduced by Simandoux (1963), which is incorporated (in its modified form) as a shaly sandstone option in PfEFFER. The Simandoux equation is: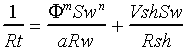

where Rt is the formation resistivity, Rw is the formation water resistivity, Rsh is the shale resistivity, F is the porosity, a, m, and n are the Archie equation constants, Vsh is the fraction of shale, and Sw is the water saturation.

The second, and more recent, model is based on the ionic double-layer observed in shaly sandstones. In reality, the conductivity of the shale component is a function of cation exchange capacities of the various types and abundances of clay minerals which are present. Since the cations are exchanged primarily at broken bonds on the edges of flakes or by lattice substitutions on cleavage surfaces, the phenomenon tends to be surface-area dependent rather than controlled simply by the volume of clay minerals. This implies that a fine grained clay has a higher exchange capacity than a coarser grained form of the same clay volume, and this observation is confirmed by experimental data. Since all the shale indicators estimate (at best) the volume of the shale component, no explicit assessment is made of the grain size or clay mineralogical variation. Although these factors are widely known among log analysts, it is difficult to design log analysis procedures to accommodate them, in the absence of a tool that measures cation exchange capacity directly. Consequently, the model equations that use cation-exchange data have been modified to variants that substitute quantities that can be measured on logs as surrogate variables. The most widely known of these is the "dual-water model" introduced by Clavier et al. (1977) which, when generalized, takes the form of: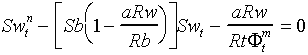

where
and
where
and the additional terms: Rb is bound water resistivity, Sb is bound-water saturation, Swt is total water saturation (including Sb), Ftsh is shaleporosity (some weighted average of the neutron and density porosities of shale), Fe is effective porosity, Ft is total porosity (including shale porosity term). The Dual-water equation is used as an alternate option for shaly sandstone water saturation estimation within PfEFFER.

Although the Simandoux and Dual-water equations were developed from different models, they do have a number of features in common (and with many other shaly sandstone equations). These are the characteristics that:

1. at zero shale content, the equations collapse to the Archie equation
2. the equation forms are polynomial functions of water saturation (and solved as such in PfEFFER, although often approximated by quadratics in other programs),
3. theinput shale properties are typically drawn from shales between the reservoir units which may not be representative of clays within the reservoir zones.

The implementation of the two shaly sandstone models within PfEFFER was made to honor two important criteria:

1. Archie equation constants can be modified interactively but, more importantly, the shale parameters of resistivity, porosity, or the means of computing shale volume can be evaluated in totally water-saturated sections , so that shale calibrations become keyed to clay mineral properties of the reservoir itself, rather than shales outside the reservoir. We term this process "internal calibration" as distinct from "external calibration" which would be tied to values of "external shales".
2. To allow Pickett plots to be made in which the conductivity effects of clays had been eliminated, and so allow petrofacies pattern recognition to be conducted free of disruptive shale effects. This concept was introduced by Aguilera (1990). If the shaly sandstone equation model designed by the user is successful, then a "corrected" resistivity can be computed that predicts the resistivity the rock would have if the clays had no conductivity effects. On the Pickett plot, the crossplot of effective porosity (porosity corrected for shale effects) and shale-corrected resistivity allows the evaluation of patterns and trends in terms of pore-sizes, geometries, fluid saturations, capillary pressure, hydrocarbon column, etc. from a similar perspective to shale-free sections.

The "shale effect" can be seen more clearly by showing the expected Pickett plot for a hypothetical sequence of shaly sandstones with water saturations of 100%, where the reduction in resistivity is predicted by application of the Simandoux equation. The magnitude of the increase in theoretical water saturation can be seen to be a function of both increasing shale content and decreasing porosity. A similar effect can be seen when using the dual-water model.

The PfEFFER implementation of the shaly sandstone models has a variety of powerful features. The models can be called consecutively or run in combination with continuous updating that responds to changes made in the shale volume, and porosity columns, as well as the parameter cell values. It should always be remembered that the Simandoux and Dual-Water solutions are only models, but the immediate interactivity and graphic displays of PfEFFER allow the user tremendous latitude in adjusting inputs to the analysis, so that the limitations of the model can be overcome to some extent by customizing the equation parameters to match local reservoir conditions.