PfEFFER Concepts Capillary Pressure

Capillary Pressure Applications

The use of critical bulk volume water (BVWi) is an empirical application of relationships that are actually controlled by capillary pressure, height of hydrocarbon column, density difference between hydrocarbon and formation water, and other physical properties of a mixed fluid/solid system. Critical BVW concepts are highly effective as aids in assessing productivity but ultimately are simple rules-of-thumb based on field experience. Because bulk volume water is the product of porosity and water saturation, BVW contours are constrained to be straight lines on Pickett plots. As such, the contours can only be trend approximations of real relationships in reservoirs. The laboratory measurement of capillary pressure data on representative reservoir core samples gives explicit information on reservoir properties that reflect pore throat sizes and their control on hydrocarbon saturation and its variation with height in a hydrocarbon column. This information can be mapped directly onto the Pickett plot as discussed below.

Laboratory measurements of capillary pressure reflect the size of pore-throats and their distribution in the rock sample. The procedure most commonly injects mercury under increasing pressure and tracks the change in mercury saturation at each increment of pressure increase. The relationship between the radius of a pore-throat accessible in the mercury/air system and the pressure is given by:

Conversion from the capillary pressures of the laboratory mercury/air system to those of the hydrocarbon/water system within the reservoir utilizes equations that require values for contact angles and interfacial tensions of the components. However, more commonly, laboratory capillary pressures are converted directly into the equivalent height of hydrocarbon that would exert the same buoyancy pressure. This additional step calls on density values for the hydrocarbon and formation because their difference controls buoyancy pressure. Values for all these parameters can be estimated for conversions that are tailor-made for specific reservoirs. Alternatively, “average” values can be compounded into a single conversion constant that is an approximate, but reasonable first order relationship to transform P, the capillary pressure in a mercury/air system to h, the height of hydrocarbon column. For a “typical” oil, a usable relationship is: h = 0.7 x P

and for gas: h = 0.35 x P

A schematic picture of capillary pressure curves is shown in the upper part of Figure 19, where changes in fluid saturation are graphed against capillary pressure and its equivalent height of hydrocarbon column for three hypothetical core plugs. The three plugs have different porosities but are from a single petrofacies where samples with higher porosities have lower “irreducible” water saturations. The curves are shown in their convention format of saturation-pressure axes. However, the same information may be remapped onto a crossplot with porosity and water saturation axes, as shown in the lower part of Figure 19. This form of presentation is less common, but has been used since at least the fifties when Stewart (1957) reported its application to pay estimation in carbonate reservoirs. The linkage of the remapped points with lines represents the same result that would be obtained by interpolating between the original capillary pressure curves. Interpolation is appropriate when the samples are considered to be from the same petrofacies.

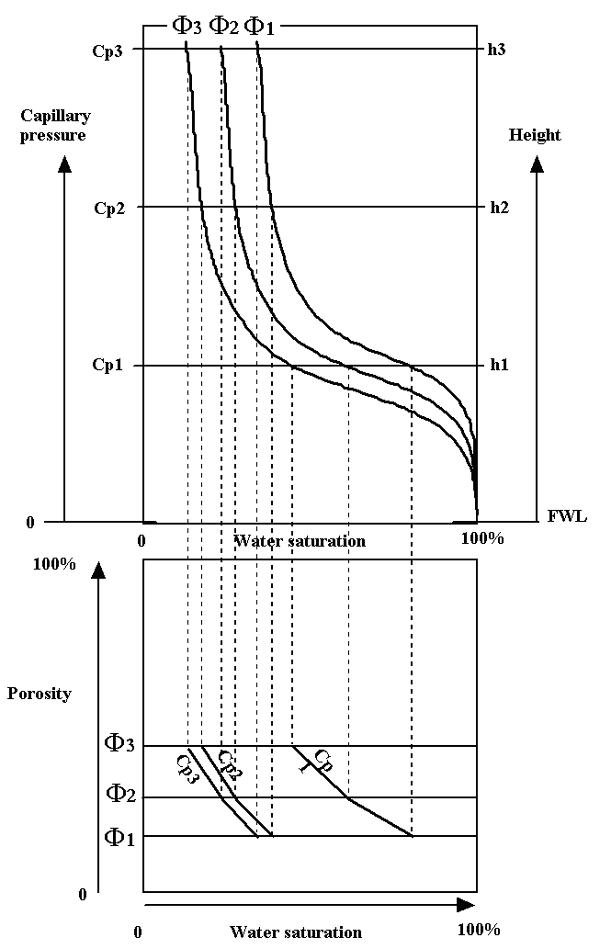Figure 19: Mapping capillary pressures(or height of hydrocarbon column) to a porosity - water saturation crossplot.

Notice that the crossplot has the same axes as the “Buckles plot” and that the capillary pressure contours conform approximately with hyperbolae that track with constant bulk volume water values. This shows that the productivity/pore size concepts of critical BVW are simply empirical expressions of phenomena controlled by pore throat distributions, capillary pressure, and hydrocarbon column. Notice also that although the capillary pressures are sampled at equal intervals of height, their mapping on the crossplot shows a rapid convergence on a stable boundary where BVW changes only gradually over relative large values of reservoir height.

Mapping of capillary pressure contours onto the Pickett plot

If capillary pressure data can be mapped in porosity -water saturation space, then they can be mapped on the Pickett plot where the water saturation axis is oblique to the porosity axis (Figure 20). For a perfect “Buckles rock”, the pressure contours would follow BVW lines exactly. Otherwise, the contours will follow curved paths that reflect the overall changes in pore-throat distributions with volume of porosity. If samples from radically different petrofacies are mapped collectively, the result will show abrupt changes and disruptions in the contour trends. Essentially, the breaks make the point that the interpolations are invalid and that the samples should be subdivided between sets that produce more harmonious pressure trends. The subdivisions constitute different petrofacies but they are a direct reflection of flow unit types since the differences are controlled by pore-throat distributions. Therefore, mapping of capillary pressure data onto a Pickett plot may be an immediate “answer” to productivity and permeability when the reservoir unit consists of a single petrofacies. However, the method becomes a valuable tool in its own right as a means to differentiate multiple petrofacies/flow units in a heterogeneous reservoir.

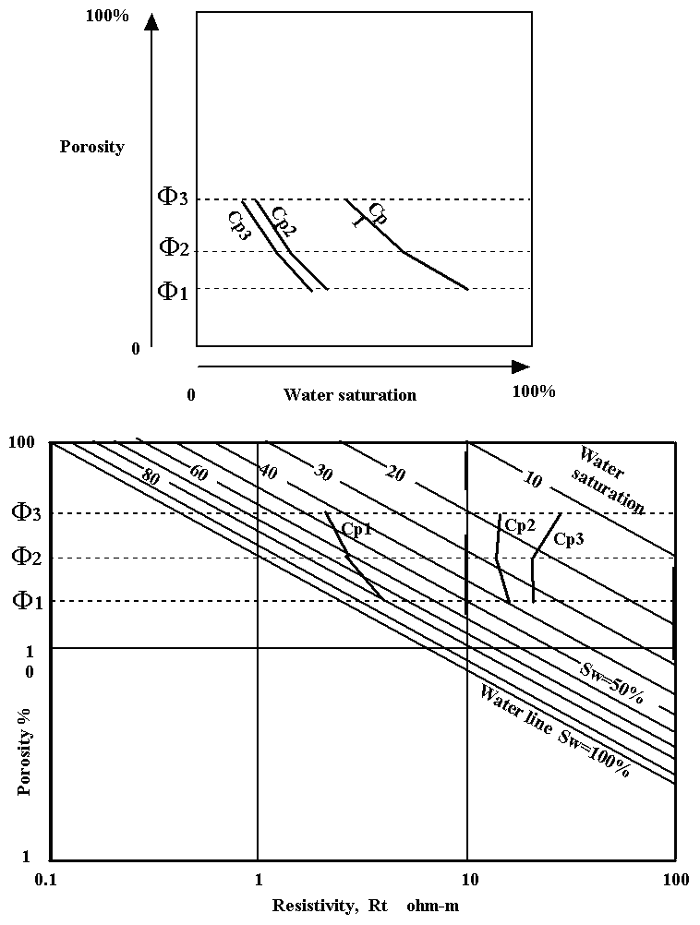Figure 20: Alternative mappings of capillary pressure in porosity - water saturation space: orthogonal axes (above); oblique Pickett plot axes (below).