PfEFFER Concepts Permeability Prediction

Permeability Prediction from Wireline Logs

The most simple quantitative methods to predict permeability from logs have been keyed to empirical equations of the type : where P and Q are constants determined from core measurements, and applied to log measurements of porosity (F) to generate predictions of permeability (K). The relationship is linearized if the equation is logarithmically transformed to:

When applied to special cases of homogeneous sandstones, the results may be adequate, but prediction errors are often large in typical sandstones, and the errors in predicted permeability commonly range across orders of magnitude when applied to carbonates. The reason for this is that permeability is not exclusively determined by pore volume, but is also controlled by internal surface area, pore network tortuosity, pore throat geometry and other variables.

If a usable relationship can be developed between permeability and porosity, then the results can be plotted directly on the Pickett plot as permeability contours that track directly on their associated porosity value. This simple equivalence results because the equation gives a unique permeability prediction value for each porosity value. The predictions from these lines will only hold true in situations where the grain/pore size does not vary much.

Changes in pore size will influence permeability because they are accompanied by corresponding changes in internal surface area. Smaller pore sizes generate larger surface area and a matching reduction in permeability; larger pore sizes are linked with higher permeabilities. The interrelationships are contained in the classic Kozeny-Carman equation :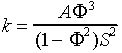

which incorporates the specific surface area, S, as an additional variable to estimate permeability.

The specific surface area is the ratio of surface area to volume of framework solid and is difficult to measure directly by conventional methods. However, the specific surface area is inextricably linked with pore size, which in turn controls irreducible water saturation. Wyllie and Rose (1950) proposed a modification of the Carman-Kozeny equation that substituted irreducible water saturation for the specific surface area term: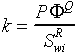

The irreducible water saturation term in the modified equation functions as a powerful surrogate variable for specific surface area, and this accounts for the improvement in permeability estimates when incorporated with porosity.

The Wyllie-Rose relationship is a generalized equation that requires the determination of values for the constants P, Q, and R to be calibrated from core measurements. Probably the most widely-used version of this equation is the “Timur equation” for sandstones. Timur (1968) developed an equation which linked permeability with both porosity and irreducible water saturation Swi in sandstones, based on laboratory measurements of core. The results showed a considerable improvement in permeability estimation over those based on porosity values alone. However, notice that the use of irreducible water saturation as an input variable restricts the predictions to hydrocarbon reservoir zones.

Addition of predicted permeability contours to the Pickett plot

Solutions to equations of the Wyllie-Rose type can be plotted as predicted permeability lines directly on the Pickett plot, because a logarithmic transformation of the equation leads to:

As an example, contours of permeability as predicted by the Timur equation are drawn on the Rottweiler Sandstone Pickett plot in Figure 18. If zones A to E are at irreducible water saturation, then their predicted permeabilities can be read directly from interpolation between the permeability contours. If zone F is a transition zone with the same pore structure as the reservoir zones, then its permeability will be found by moving along the porosity line to the irreducible trend and reading the matching permeability value. If, however, Zone F is not a transition zone but is at irreducible saturation, then the permeability can be read directly. The permeability will be lower than in the first alternative, because its relatively higher water saturation would imply that the pore size was finer.

In PfEFFER, the Timur equation values are entered as default values of P, Q, and R. Unless the default values are modified, permeability prediction lines will be drawn based on this equation. It should always be remembered that the Timur relationship was developed for sandstones. An equivalent general formula for carbonates is unrealistic because of the high variability of carbonate pore geometries. However, equivalent relationships for specific carbonate pore types should be feasible, based on the analysis of core measurements.

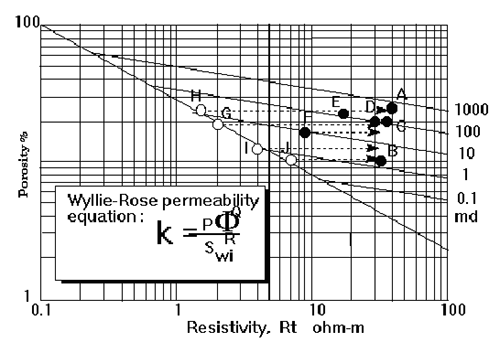Figure 18: Permeability contours drawn on Pickett plot of Rottwieler Sandstone data, using a Wyllie-Rose releationship with both porosity and irreducible water saturation. The contours honor the Timur equation form which was developed for sandstones.