

|
PfEFFER ConceptsArchie Equations |
Fifty years after it was introduced, the Archie equation remains the keystone of log analysis for the solution of water saturation of potential oil and gas zones:
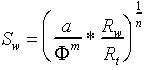
The equation is actually made up of two separate equations. The first describes the relationship of the ratio of the resistivity of a water saturated rock, Ro, to its formation water resistivity, Rw, to the fractional porosity, F:
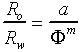
This resistivity ratio is also known as the “formation factor”, F. The second equation relates the ratio of the observed formation resistivity, Rt, to its expected resistivity, Ro, if it was completely saturated with water, to the fractional water saturation, Sw:
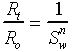
The equations are universally applied to reservoir fluid calculations from wireline logs in “clean” (shale-free) formations. Even when specialized equations are applied to clastic reservoirs that are markedly shaley, these same equations are adaptations of the Archie equation that accommodate shale effects.
The application of the Archie equations presuppose a knowledge of the parameters, or at least reasonable estimates of them, in order to calculate acceptable water saturations. Formation water resistivity can usually be established from field measurements and/or log analysis estimations. However, the quantities of a, m (the “cementation factor”), and n (the saturation exponent) are usually unknown and their values are given as a matter of experience. The range of values for m and their relationship with rock texture has been the subject of much measurement and discussion. By contrast, the variability of n is less well understood, but is generally taken to be the number 2 (at least, in water-wet zones). The problem is further compounded by the realization that these “constants” are only likely to remain so in relatively homogeneous reservoirs, where rock texture and pore geometry remain fairly uniform. Continuing advances in theory and measurement demonstrate that simple models may be poor (and puzzling) representations, or even downright misleading in heterogeneous and complex reservoirs that are the targets of many of today’s energy companies.
A direct solution for water saturation is predicated on a knowledge of both the formation water resistivity and the constants of the Archie equation. There are many occasions when either or both of these quantities are unknown. There will also be situations where, for example, the Humble form of the Archie equation will not be deemed a satisfactory approximation for evaluation of relatively tight sandstones, or the "limestone" form of the equation adequate for certain carbonates. However, both water resistivity and an appropriate form of the Archie equation may be deduced from logs provided that some zones with 100% water saturation occur in the unit of interest. This is not usually a difficult stipulation to meet since many productive units will have a hydrocarbon/water contact separating the reservoir from a lower, water-saturated section. Failing this, an adjacent water-saturated unit of similar lithology and (hopefully) with similar water resistivity may be used as a surrogate for the critical zones. These critical water zones do not have to be recognized initially, but will manifest their presence (or absence) in the methods of analysis described in the following pages.
The zone readings of porosity and resistivity of the hypothetical “Rottweiler Sandstone” (Figure 1) can be used to demonstrate log analysis procedures for varying degrees of uncertainty, and how these techniques are enhanced considerably when used in PfEFFER within GEMINI.
If the Archie equation constants in Rottweiler Sandstone samples were determined as a=1 and m=1.8, n=2, while the formation water resistivity in the formation was 0.10 ohm-m at formation temperature, then:
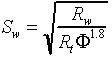
Applied to the zone readings:
| Zone |
Rt |
f% |
Sw |
Sh |
| A | 39 |
24 |
0.18 |
0.82 |
| B | 31 |
10 |
0.45 |
0.55 |
| C | 36 |
20 |
0.22 |
0.78 |
| D | 30 |
20 |
0.25 |
0.75 |
| E | 19 |
22 |
0.28 |
0.72 |
| F | 9 |
18 |
0.49 |
0.51 |
| G | 2 |
19 |
1.00 |
0.00 |
| H | 1.5 |
23 |
0.97 |
0.03 |
| I | 4.0 |
12 |
1.07 |
-0.07 |
| J | 7 |
10 |
0.95 |
0.05 |
The reconnaissance water resistivity
(Rwa) technique is the most
widely used method under these conditions.
Now, F = a/fm ( the Archie equation) and F = Ro/Rw (by definition)
Therefore, Rw = Ro fm/a
By analogy, Rwa = Rt fm/a
Note that for any zone: when Sw = 1, Rwa = Rw
and when Sw < 1, Rwa > Rw
If the Archie equation constants are known, Rwa values may be calculated from the resistivity and porosity log readings. Within the oil or gas reservoir section, these values will be high and will fluctuate in sympathy with variations in water saturation. Below the hydrocarbon/water contact or in adjacent , similar water-wet units, the values will tend to stabilize at a lower limiting value which corresponds to an estimate of the true formation water resistivity, Rw.
In the Rottweiler Sandstone example, F=1/F1.8 and so the equation for Rwa is:
![]()
So the zone values of Rt and F can be transformed into Rwa values:
Zone |
Rt |
f% |
Rwa |
A |
39 |
24 |
2.988 |
B |
31 |
10 |
0.491 |
C |
36 |
20 |
1.987 |
D |
30 |
20 |
1.656 |
E |
19 |
22 |
1.245 |
F |
9 |
18 |
0.411 |
G |
2 |
19 |
0.101 |
H |
1.5 |
23 |
0.106 |
I |
4 |
12 |
0.088 |
J |
7 |
10 |
0.111 |
It is fairly obvious that the water zones are G, H, I and J. A representative value can be picked out by eye and would be a value of about 0.1 ohm-m.
In PfEFFER, the reconnaissance water resistivity values are stored in column RWA of the Computational section. When the user has selected an Rwa value that appears to be a reasonable estimate of the actual formation water resistivity, Rw, this number should be typed into the RW cell in the PARAMETERS box. Water saturations and other quantities will then be recomputed automatically in the Home Area.
The reconnaissance cementation
exponent (ma) method can
be used, and has conceptual similarities with the Rwa technique.
Now, F = a/fm ( the Archie equation)
and F = Ro/Rw (by definition)
If the formation water resistivity, Rw, is known and the Archie equation constant, a is assumed to be of unit value ( a = 1), then:
m = log(Rw/Ro) /log (f)
By analogy, ma = log(Rw/Rt) /log (f)
Note that for any zone: when Sw = 1, ma = m
and when Sw < 1, ma > m
In the Rottweiler Sandstone example, the formation water resistivity, Rw = 0.1
So the zone values of Rt and F can be transformed into ma values:
Zone |
Rt |
f% |
ma |
A |
39 |
24 |
4.18 |
B |
31 |
10 |
2.49 |
C |
36 |
20 |
3.66 |
D |
30 |
20 |
3.54 |
E |
19 |
22 |
3.47 |
F |
9 |
18 |
2.62 |
G |
2 |
19 |
1.80 |
H |
1.5 |
23 |
1.84 |
I |
4 |
12 |
1.74 |
J |
7 |
10 |
1.85 |
In PfEFFER, the reconnaissance cementation exponent values are stored in column MA of the Computational section. When the user has chosen an MA value that appears to be a reasonable estimate of the Archie equation cementation exponent (based on BOTH the calculated values AND expectations for the reservoir rock type), this number should be typed into the M cell in the PARAMETERS section.
It would be rare for the log analyst to be confronted by a situation where the Archie equation parameters and formation water resistivity were completely unknown. However, it is very common that the parameters are known to either a lesser or greater degree of uncertainty, particularly as the Archie "constants" will show some degree of variability in even mildly heterogeneous formations. In the next two sections, we discuss the use of the Pickett resistivity-porosity crossplot as a powerful graphical method of analysis and an application of the Hough transform in an approach that combines the reconnaissance water resistivity (Rwa) and reconnaissance cementation exponent (Ma) simultaneously.