Prev Page--Approach and Versatile soil moisture budget || Next Page--Verification, Conclusions
Hydrologic-budget Implementation and Synthesis
Having outlined the elements of the basinwide integration methodology and the VB soil-moisture accounting procedure, we will now outline the implementation steps and synthesis of the hydrologic budget for the entire watershed.
Hydroclimatic Zones
The Rattlesnake Creek watershed was subdivided into several climatic zones, based on the distribution of available NOAA climatological stations covering the watershed (fig. 4). Three precipitation stations are located in the watershed, the Hudson (Hud) station covering the northeastern portion of the watershed, the Trousdale (Trou) station covering the central portion, and the Bucklin (Buck) station covering the southwestern portion of the watershed. Only two temperature stations are located in the watershed: one, the Hudson station, covering the downstream portion of the watershed and the other, the Greensburg station, covering the upstream portion. Therefore, the watershed was divided into the following four climatic zones, where each point in each zone is closest to the named temperature-precipitation station than to any other station: Hud-Hud, Hud-Trou, Gr-Trou, and Gr-Buck (fig. 4).
Soils
Thirteen dominant soil associations (composed mainly of 18 different soil series) are found within the watershed (fig. 13). For each soil series, the available water capacity was determined from the appropriate county Soil Conservation Service soil survey to depths of 3 and 5 ft (~1 and ~1.5 m). The 3-ft (~1-m) soil depth was used to model the available soil moisture for wheat because it has a rooting depth of approximately 3 ft (~1 m). The 5-ft (~1.5-m) depth, which is generally the depth limit of the Soil Conservation Service soil surveys, was used for all other crop covers in the watershed because the highest root density of most crops is in the upper 5 ft (~1.5 m). Soil associations, soil compositions, and available water capacities for each soil are presented in table 1.
Table 1--Rattlesnake watershed soil associations and their available water capacities.
| Soil Association |
Soil Composition (as % of total) |
Available-water Capacity (in.) (5-ft depth) |
Available-water Capacity (in.) (3-ft depth) |
|
|---|---|---|---|---|
| 1 | Pratt- Tivoli (P-T) |
60 40 |
4.9 | 3.2 |
| 2 | Pratt- Carwile (P-C) |
71 29 |
7.3 | 4.7 |
| 3 | Attica- Pratt- Carwile (A-P-C) |
53 38 9 |
5.6 | 3.7 |
| 4 | Naron- Farnum (N-F) |
75 25 |
9.7 | 6.3 |
| 5 | Naron- Carwile (N-C) |
83 17 |
9.2 | 5.9 |
| 6 | Farnum- Lubbock (F-L) |
70 30 |
11.2 | 7.0 |
| 7 | Blanket- Farnum (B-F) |
56 44 |
11.2 | 6.9 |
| 8 | Natrustolls- Plevna (Na-Pl) |
65 35 |
9.7 | 6.1 |
| 9 | Carwile- Farnum- Tabler (C-F-T) |
42 36 22 |
10.3 | 6.3 |
| 10 | Zenda- Hord- Waldeck (Z-H-W) |
43 37 20 |
9.2 | 6.1 |
| 11 | Harney- Uly (H-U) |
89 11 |
11.4 | 7.2 |
| 12 | Holdredge (Hol) |
100 | 10.8 | 6.7 |
| 13 | Dillwyn- Tivoli (D-T) |
65 35 |
4.4 | 2.8 |
Given the sandy nature of most soils in the basin, a Z table typical of sandy soils (curve F in fig. 16) was chosen. The Z table represents the relationship between the ratio of AE/PE and the plant-available soil moisture. This ratio remains constant from 100% to 30%, below which the AE/ PE ratio declines sharply as an exponential decay-form relationship with the drying of the soil.
Figure 16--Various proposals for relationships between AE:PE ratio and available soil moisture (from Baier et al., 1979).
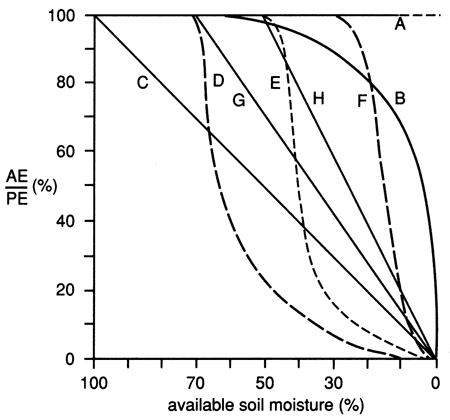
The water-budgeting procedure was initiated a month before the planting period, with the soil at its maximum available water capacity. This initial condition allowed the soil-available water capacity to equilibrate with the local climatic conditions before the time period of interest. In cases of a crop rotation with a summer second crop, a near zero deficit date near the second crop planting period was chosen as the initial soil-moisture condition, as will be described below.
Crops
In the Rattlesnake watershed the dominant crop types are winter wheat, sorghum (or milo), alfalfa, soybeans, and corn. Common agricultural practices in the watershed include crop rotation and strip farming. The following crop-rotation practices were incorporated into the water-budgeting procedure for 1982-83: winter wheat-sorghum (both irrigated and dryland), winter wheat-soybeans (both irrigated and dryland), fallow-winter wheat (both irrigated and dryland), fallow-corn, and continuous alfalfa (both irrigated and dryland). Fallow conditions were simulated during the time periods before planting and after harvest of the various crops. Winter wheat, natural growth (grasses), and alfalfa have dormancy periods simulated during the winter months. For crop rotations in which two crops with different rooting depths are involved, such as the wheat-sorghum or wheat-soybean combinations, one of two procedures outlined in appendix I was used.
The vegetation parameters are represented by crop coefficients. Each soil "zone" has a coefficient for each stage of crop growth. At different plant-growth stages, the roots can utilize the moisture in the soii profile at different depths and rates. Crop coefficients adopted for natural growth (simulated as brome grass), alfalfa, soybean, and corn are those presented in Baier et al. (1979). Crop coefficients for winter wheat were modified from Baier et al. (1979) and Vanderlip and Brown (1974). Crop coefficients for sorghum were calculated from grain sorghum data by Jensen (1968). The various crop-growth stages and corresponding dates, as well as the crop coefficients adopted for this report, are presented in appendix II.
Irrigation
Irrigation amounts for various crops were based on the Soil Conservation Service Kansas Irrigation Guide (U.S. Department of Agriculture, 1977) for the study area, in conjunction with interviews with local county Soil Conservation Service (SCS), Agricultural Stabilization and Conservation Service (ASCS), and extension irrigation specialists. These irrigation amounts are shown in table 2. Center-pivot sprinklers are the predominant method of water application for irrigation in the watershed. Through discussions with local specialists, we concluded that it takes approximately three days on average for a sprinkler system to complete one revolution and that approximately 0.25-0.5 inch (0.64-1.27 cm) of water is applied per sprinkler revolution. Therefore, in simulating irrigation applications for the daily water-budgeting procedure, water is assumed to be applied in 0.5-inch (1.27-cm) increments with successive irrigation applications at three-day intervals.
The Soil Conservation Service (SCS) Kansas Irrigation Guide (U.S. Department of Agriculture, 1977) was followed for determining the monthly distribution of irrigation applications as percentages of the seasonal totals based on 80% chance rainfall, as shown in table 3. The irrigation-application dates employed in the water-balance simulations also are shown in table 2.
Table 2--Irrigation applications and dates.
| Crop | Total Irrigation (inches) |
Irrigation-application Dates (month/day) |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Corn | 15.0 | 1983 | 5/11 | 5/27 | 6/07 | 6/11 | 6/15 | 6/18 | 6/21 | 6/24 | 6/27 | 6/30 |
| 7/03 | 7/06 | 7/09 | 7/12 | 7/15 | 7/18 | 7/21 | 7/24 | 7/27 | 7/30 | |||
| 8/02 | 8/05 | 8/08 | 8/11 | 8/14 | 8/17 | 8/20 | 8/23 | 8/26 | 8/29 | |||
| Alfalfa | 23.5 | 1982 | 10/5 | 10/12 | ||||||||
| 1983 | 4/20 | 4/27 | 5/03 | 5/08 | 5/13 | 5/18 | 5/23 | 5/31 | 6/06 | 6/09 | ||
| 6/12 | 6/15 | 6/18 | 6/21 | 6/24 | 6/27 | 6/30 | 7/03 | 7/06 | 7/09 | |||
| 7/12 | 7/15 | 7/18 | 7/21 | 7/24 | 7/27 | 7/30 | 8/02 | 8/05 | 8/08 | |||
| 8/11 | 8/14 | 8/17 | 8/20 | 8/23 | 8/26 | 8/29 | 8/31 | 9/03 | 9/06 | |||
| 9/09 | 9/13 | 9/17 | 9/23 | 9/29 | ||||||||
| Winter wheat |
6.0 | 1982 | 10/23 | 11/15 | ||||||||
| 1983 | 3/11 | 4/10 | 4/16 | 4/25 | 5/02 | 5110 | 5/17 | 5/24 | 5/30 | 6/06 | ||
| Sorghum | 12.5 | 1983 | 6/17 | 7/01 | 7/04 | 7/07 | 7/10 | 7/13 | 7/16 | 7/19 | 7/22 | 7/25 |
| 7/28 | 7/31 | 8/03 | 8/06 | 8/09 | 8/12 | 8/15 | 8/18 | 8/21 | 8/24 | |||
| 8/27 | 8/30 | 9/02 | 9/05 | 9/08 | ||||||||
| Soybean | 12.0 | 1983 | 7/01 | 7/04 | 7/07 | 7/10 | 7/13 | 7/16 | 7/19 | 7/22 | 7/25 | 7/28 |
| 7/31 | 8/03 | 8/06 | 8/09 | 8/12 | 8/15 | 8/18 | 8/21 | 8/24 | 8/27 | |||
| 8/30 | 9/02 | 9/05 | 9/08 | |||||||||
Table 3--Monthly distribution of net irrigation requirements, in percent of seasonal total based on 80% chance rainfall.
| Crop | April | May | June | July | August | September | October | Total |
|---|---|---|---|---|---|---|---|---|
| Alfalfa | 5.1 | 12.7 | 17.8 | 24.6 | 21.6 | 13.1 | 5.1 | 100 |
| Corn | 1.4 | 22.9 | 43.1 | 32.6 | 100 | |||
| Sorghum | 1.7 | 44.6 | 41.3 | 12.4 | 100 | |||
| Soybeans | 24.4 | 52.0 | 23.6 | 100 |
| Crop | October | November | March | April | May | Total | |
|---|---|---|---|---|---|---|---|
| Wheat | 8.2 | 10.9 | 13.6 | 30.0 | 37.3 | 100 | |
| Year 1 | Year 2 | ||||||
Basinwide Integration
The VB water-budgeting procedure was applied to each soil series and crop-cover combination in each hydroclimatic zone in order to obtain daily values of the water-balance components within the 1982-83 period of interest. These hydrologic components, valid for each soil series, were then combined into soil-association components using the ratio of each soil series within the soil association as the ratio of the hydrologic components within their respective soil association. Thus, for a soil association consisting of two soil series,
![]()
in which ![]() = composite average of hydrologic component i for soil series A and B; Aa and Ab are the percent of soil series A and B, respectively; and Ca and Cb are the hydrologic component i for soils A and B, respectively.
= composite average of hydrologic component i for soil series A and B; Aa and Ab are the percent of soil series A and B, respectively; and Ca and Cb are the hydrologic component i for soils A and B, respectively.
The composite components of the water balance were expressed in units of length (inches) over a unit area. The areas of each soil association and type of vegetation cover within each soil-association area were then determined. Soil-association areas within the watershed were measured with an areal planimeter. However, no data specifying areas and types of different crop growth within each soil association in the watershed were available. To overcome this problem, the following procedures were followed. First, all irrigation wells within the watershed were plotted from water-rights records available from Groundwater Management District No. 5 and the Division of Water Resources of the Kansas State Board of Agriculture. The irrigated acreage and the total number of irrigation wells within each county in south-central Kansas were obtained from Cooperative Extension Service surveys and the 1982-83 Kansas Farm Facts report (1985). An average of 129 acres per well was found to be irrigated. Thus, by shading an equivalent area around each well, the irrigated cropland within each soil association of the watershed was approximated.
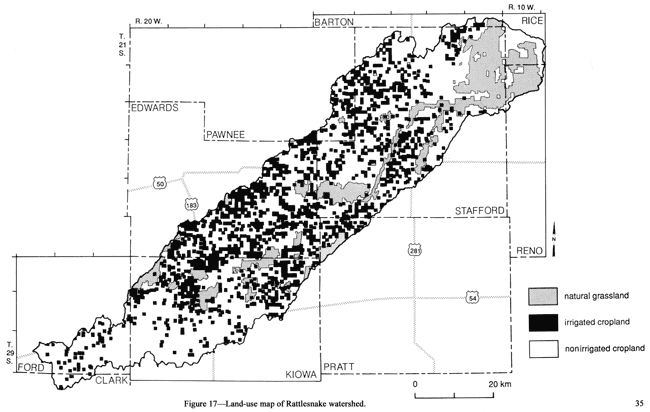
Second, from a 1974 land-use and land-cover map of south-central Kansas (U.S. Geological Survey, Land Use Series Map L-28, 1979), rangeland (grassland) within the watershed was determined assuming that these areas had not been significantly altered by 1982-83; what significantly changed was the proportion of irrigated versus nonirrigated cropland. Third, the remaining areas of the watershed represent predominantly nonirrigated cropland and pasture land. In this manner, the entire watershed, and thus each soil association, was subdivided into three different zones of vegetation cover (fig. 17), namely irrigated cropland, rangeland, and combined nonirrigated cropland and pasture land. These are tabulated in table 4.
Table 4--Land-use acreages for each soil association and climatic zone within the Rattlesnake watershed during 1982-83.
| Climatic Zone |
Soil Assoc. |
Total Area (mi2) |
Rangeland (mi2) |
Irrigated Land (mi2) |
Dryland Cropland and Pasture (mi2) |
|---|---|---|---|---|---|
| Hudson-Hudson | P-T | 49.0 | 24.2 | 5.4 | 19.4 |
| P-C | 206.0 | 7.5 | 42.0 | 156.5 | |
| N-F | 49.9 | 1.0 | 14.1 | 31.8 | |
| N-C | 68.3 | 0.0 | 18.1 | 50.2 | |
| B-F | 12.1 | 0.0 | 1.6 | 10.5 | |
| NA-Pl | 59.3 | 59.3 | 0.0 | 0.0 | |
| C-F-T | 15.2 | 3.5 | 0.0 | 11.7 | |
| D-T | 82.2 | 75.2 | 1.0 | 6.0 | |
| Hudson-Trousdale | P-T | 37.4 | 25.8 | 3.6 | 8.0 |
| P-C | 46.2 | 1.5 | 12.3 | 32.4 | |
| N-F | 33.4 | .3 | 7.0 | 26.1 | |
| N-C | 63.7 | 1.7 | 15.7 | 46.3 | |
| NA-Pl | 19.7 | 19.7 | 0.0 | 0.0 | |
| Greensburg-Trousdale | P-T | 99.8 | 58.2 | 20.9 | 20.7 |
| A-P-C | 167.8 | 7.7 | 65.9 | 94.2 | |
| N-F | 32.2 | 0.0 | 4.6 | 27.6 | |
| N-C | 64.2 | 0.0 | 25.7 | 38.2 | |
| F-L | 42.3 | 0.0 | 13.9 | 28.4 | |
| Z-H-W | 5.8 | 0.0 | 1.0 | 4.8 | |
| Greensburg-Bucklin | P-T | 24.4 | 17.8 | 4.6 | 2.0 |
| A-P-C | 62.2 | 1.0 | 21.1 | 40.1 | |
| H-U | 177.5 | 1.0 | 18.1 | 158.4 | |
| Hol | 36.5 | 0.0 | 5.0 | 31.5 |
Figure 17--Land-use map of Rattlesnake watershed.
The Kansas State Board of Agriculture 1982-83 Farm Facts report (1985) provides acreages of each major irrigated and nonirrigated crop, as well as the pasture-land acreage for each county in the watershed. Three counties (Stafford, Edwards, and Kiowa) were chosen to represent all other counties in the watershed based on their large areal coverage within the watershed (more than 82%). Ratios of specific crops were determined within the three above-mentioned vegetation types. We assumed that the ratios or percentages of different crops in any soil association were the same as those within the county.
The areal extent of irrigated cropland, combined pasture and nonirrigated cropland, and rangeland within each soil association can then be estimated using the grid-percentage technique. A grid is placed over a known area and the number of nodes covering each subarea are counted and converted into a percentage of the total nodes covering the area. The known area can then be subdivided by the percentages calculated above.
The percentages of the different irrigated and nonirrigated crops are known for the county, and therefore (by assumption), for each soil association, as well as the corresponding areas of the three general types of vegetation cover (irrigated and nonirrigated cropland, and rangeland). Specific crop acreages can thus be determined. The pastureland acreage (known from Farm Facts figures for each county) was separated from the combined pasture-nonirrigated cropland category and then added to the rangeland acreage for simulation purposes because pasture and rangeland were both simulated as natural growth or grassland in the VB procedure.
A utility program was employed to sum the components of the water balance in acre-feet units for the different types of vegetation areas of the watershed. The required input data were soil-association areas for irrigated cropland and nonirrigated cropland, ratios of specific nonirrigated crops within the respective county, and each composite hydrologic component for each soil association. The program output consisted of tables of each hydrologic component according to vegetative type and soil association, as will be discussed in the results and discussion section.
The hydrologic-component data before and after the above compilation were added by another utility program to check for input errors and to determine the range of error within the calculations. The utility program calculated the hydrologic-balance-equation error as
PCP + SD - AE - DR - RO = error (4)
where PCP = precipitation
SD = soil-moisture deficit
AE = actual evapotranspiration
DR = deep drainage, and
RO = surface runoff.
Large errors were considered to be input errors and were traced to their cause and corrected. Small errors, generally less than 1% of total precipitation, were considered to be due to cumulative rounding errors.
The compiled data consisting of the components of the water balance in acre-feet were then used to estimate the total-watershed amounts of each hydrologic component in the balance equation by simply adding each component over the entire watershed.
A separate utility program was employed to calculate the average value of the water-balance components (in units of length) for the respective areas of irrigated cropland, nonirrigated cropland, and grassland within each soil association. These data were then displayed in the form of maps of deep drainage, surface runoff, actual evapotranspiration, and soil-moisture deficit over the Rattlesnake Creek watershed and are discussed in the section on results and discussion.
The VB program was adopted to run on the Data General MV8000 (later upgraded to MV20000) minicomputer of the Kansas Geological Survey. Several modifications to the program were implemented for this study, such as increasing the number of crop-growth stages, adding irrigation amounts separately, calculating cumulative sums of the components of the water balance, and other minor changes.
Results and Discussion
Climatic, soil, crop, and land-use parameters all affect the amount and distribution of the various hydrologic variables, namely runoff, evapotranspiration, deep drainage, and soil-moisture deficit.
Climatic Factors
Solar radiation and temperature greatly affect the evaporative regime of an area; consequently, evapotranspiration varies seasonally and spatially in response to these climatic factors. Thus, during the winter period the evapotranspiration regime is at its minimum (see figs. 28-31 in temporal-patterns section following). Local climate, irrigation, variations in transpiration rates among different crops, and soil factors exert additional influences on evapotranspiration, as will be discussed later in the sections on soil factors and crops and land use.
Precipitation, the primary water-supply source in the area, exerts a major influence on the components of the hydrologic cycle. Thus, in the northeastern portion of the watershed where precipitation during the 1983 water year was lower than in other parts of the watershed (approximately 18.9 inches [48.0 cm] at Hudson compared to 23.1 inches [58.6 cm] in Trousdale and 23.5 inches [59.7 cm] in Bucklin), all hydrologic variables exhibit lower values compared to the rest of the watershed, as will be shown below.
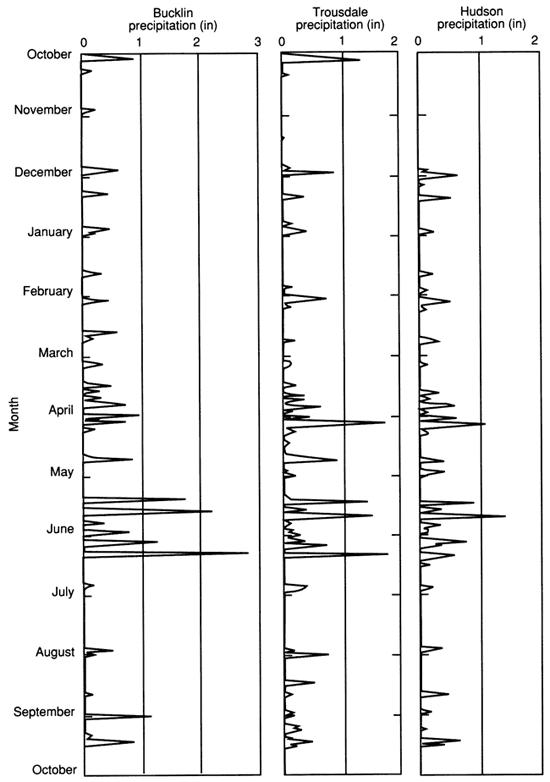
The amount, frequency, duration, and intensity of rain affects the runoff and deep-drainage hydrologic variables in particular. For example, runoff in the Greensburg-Bucklin climatic zone during the 1983 water year is higher than in the other climatic zones because of the higher frequency, intensity, and amounts of rainfall in that area compared to the other watershed areas (fig. 18).
Figure 18--Precipitation patterns at three stations in Rattlesnake watershed (1983 water year).
Soil Factors
The basic soil parameter affecting the hydrologic variables in this model is the available water capacity (AWC) of the root zone. The soil hydraulic conductivity is incorporated indirectly in the model through the choice of a Z table. However, because the detailed physics of soil-water flow are not considered in this model, the AWC of the soil exerts the dominating influence; the AWC of each soil determines the maximum limit of actual evapotranspiration that can be extracted without additional infiltration, and the maximum soil-moisture deficit possible. Thus, given the same hydroclimatic conditions and crop cover, a soil with a relatively low AWC will exhibit a relatively small water deficit, and smaller amounts of water will be lost through ET compared to losses from a soil with higher AWC (figs. 19 and 20). Final soil-moisture deficit values are not monotonically cumulative, like values of precipitation, evapotranspiration, drainage, and runoff, but are a running algebraic total (with positive and negative values). The final soil-moisture deficit total is responsive mainly to the weather conditions of the previous few weeks. The soil-moisture deficit for irrigated cropland in fig. 19 is shown to be higher than for nonirrigated cropland for soils with AWC greater than 7 inches (17.5 cm). This seemingly paradoxical result is due to the different proportions of individual crops, which cause higher or lower soil-moisture deficits in the soil (see crops and land-use section following).
Figure 19--Soil-moisture deficit versus available water capacity for grassland, dryland, and irrigated cropland for Rattlesnake watershed portion covered by Bucklin and Trousdale precipitation stations.
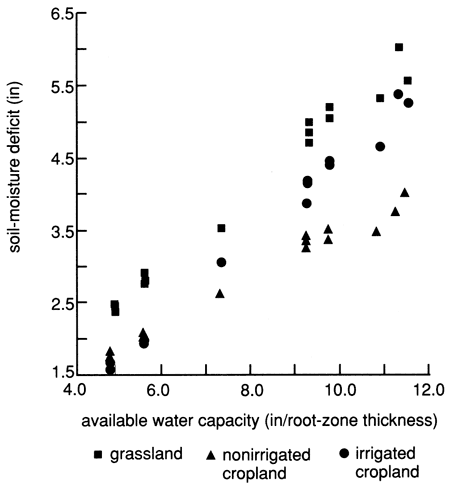
Figure 20--Actual evapotranspiration versus available water capacity for grassland, dryland, and irrigated cropland for Rattlesnake watershed portion covered by Bucklin and Trousdale precipitation stations.
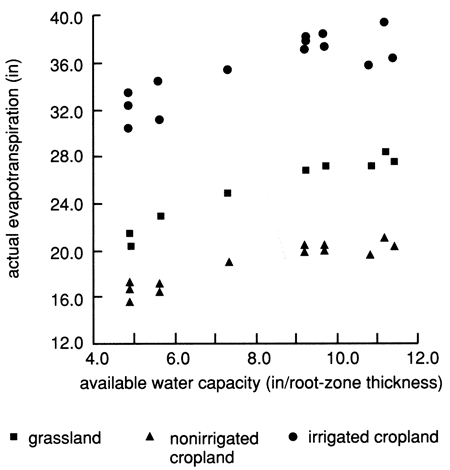
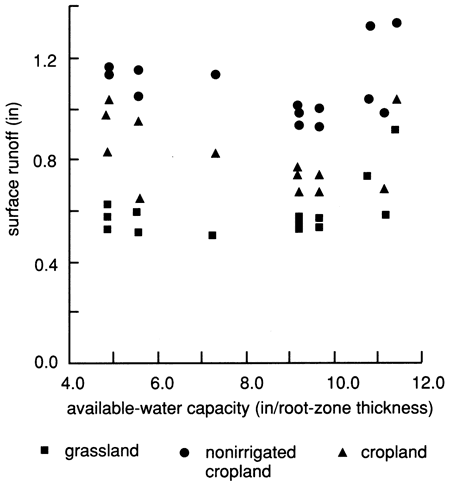
The AWC also determines the amount of water that can infiltrate into the soil before deep drainage occurs. The AWC acts as a buffer for infiltrating water. Thus, deep drainage decreases with increasing AWC (fig. 21). Given the same initial-moisture conditions, a soil with higher AWC can absorb more infiltrating water than low-AWC soils. The soil-moisture conditions, especially the current soil-moisture deficit, affect the quantity of water that can infiltrate into and run off from the various soils. However, runoff data do not show clear trends with varying AWC because of the dominance of precipitation amounts, intensity, and frequency over soil factors (fig. 22). In some instances, however, higher runoff was produced from low-AWC sandy soils than from high-AWC clayey soils, as may be seen in dryland cropland (fig. 22), indicating that a procedure governing the rate of soil-water movement is needed in the VB program.
Figure 21--Deep drainage versus available water capacity for grassland, dryland, and irrigated cropland for Rattlesnake watershed portion covered by Bucklin and Trousdale precipitation stations for Hudson climatic region of Rattlesnake basin.
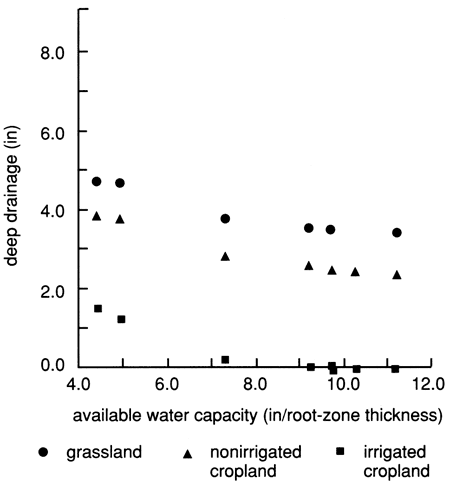
Figure 22--Surface runoff versus available water capacity for grassland, dryland, and irrigated cropland for Rattlesnake watershed portion covered by Bucklin and Trousdale precipitation stations.
Crops and Land Use
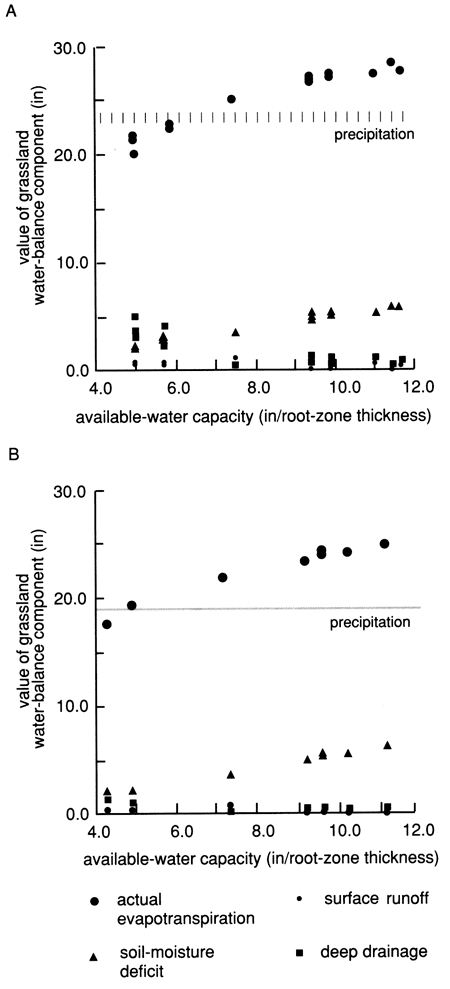
The water balance also is greatly influenced by the plant cover and land-use practice. The largest element of the water balance is the ET component, as can be seen for native grassland in fig. 23. The impact of vegetation on the hydrologic balance is complex and depends on factors such as crop coefficients, growth stages, rooting depths, soil, water, and climatic conditions as used in this simulation model.
Figure 23--Grassland water-balance components for Hudson climatic region (A) and the rest of Rattlesnake watershed (B).
The crop coefficients vary with the stage of crop growth. Mature plants have greater ability to extract soil moisture from all soil horizons and thus have larger coefficients than young plants. If the summation of crop coefficients for the different soil layers during a growth stage is equal to 1.0, AE and PE will be equal during periods of no water deficiency. If the summation is less than 1.0, plants transpire at less than the potential rate, even under well-watered conditions. When plants mature, they may transpire at greater than the potential rate because of the increase in leaf area (Dyer and Dwyer, 1982). The crop with the largest crop coefficient is alfalfa. In addition, alfalfa is continuously grown from one year to the next with multiple harvests without replanting or land fallowing. Prairie grasses have the next highest overall crop coefficients with a long growing season. The various crop coefficients adopted in this study are presented in appendix II. All other crops have lower crop coefficients and are grown only part of the year. Winter wheat is simulated from October to June with a winter dormant period and a summer (post-harvest) fallow period, or in rotation with another crop from June to October. Corn, sorghum, and soybean simulations are combined with either wheat or fallow conditions to complete the year's growth. Sorghum, soybeans, and corn are grown during the summer months when PE is at its highest and soils are naturally drier.
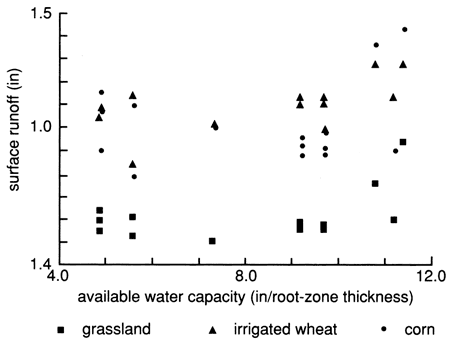
Figures 24-27 indicate some of the effects of vegetation and land-use practice on the various hydrologic variables. All other factors being equal, native grassland (and fallow land) produces the lowest runoff amounts, while irrigated cropland produces the highest runoff amounts, especially irrigated wheat/sorghum or soybean rotations and irrigated wheat (fig. 24), mainly because of the smaller rooting depth of wheat.
Figure 24--Effects of vegetation on surface runoff in Rattlesnake watershed portion covered by Trousdale and Bucklin precipitation stations.
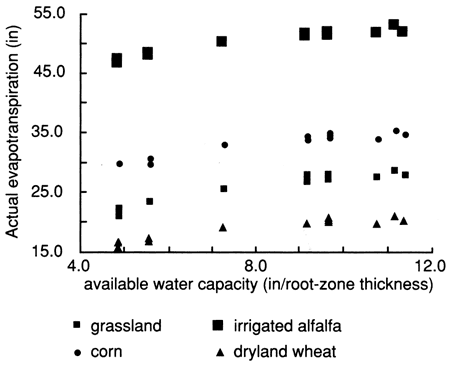
By far the highest actual evapotranspiration amounts from all crops considered in this study are produced from irrigated alfalfa acreages, followed by corn and irrigated wheat-soybean rotations, indicating the high primary productivity of these crops; the lowest amounts were produced from dryland wheat acreages (fig. 25). Note that native-grass evapotranspiration exceeds that of dryland or irrigated wheat followed by fallow or dryland sorghum or soybean. This is because of the deeper rooting system of grassland and its longer life cycle.
Figure 25--Effects of vegetation on actual evapotranspiration in Rattlesnake watershed portion covered by Trousdale and Bucklin precipitation stations.
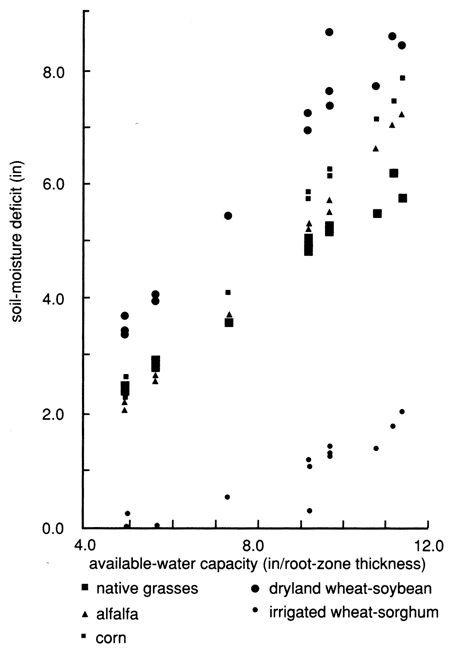
The highest soil-moisture deficit is developed in dryland wheat-soybean rotation fields, followed by corn, alfalfa, and native-grass acreages. The lowest soil-moisture deficits are developed in irrigated wheat-sorghum fields (fig. 26). A large proportion of high soil-moisture-deficit-causing crops may result in an overall higher soil-moisture deficit for irrigated cropland than for the nonirrigated cropland in the same climatic zone. For example, as shown in fig. 19, winter wheat, which causes a very low soil-moisture deficit, comprises 73% of the nonirrigated cropland, while the highest soil-moisture-deficit-causing crops, such as corn and alfalfa, are either absent or practically nonexistent (dryland alfalfa in the Hudson-Trousdale and Greensburg-Trousdale climatic zones comprises approximately 1% of the dryland crops). In contrast, the irrigated cropland includes as the major crops, the highest soil-moisture-deficit-causing crops, such as the wheat-soybean combination, corn, and alfalfa, at an overall combined proportion of 67% of the total irrigated crops.
Figure 26--Effects of vegetation on soil-moisture deficit in Rattlesnake watershed portion covered by Trousdale and Bucklin precipitation stations.
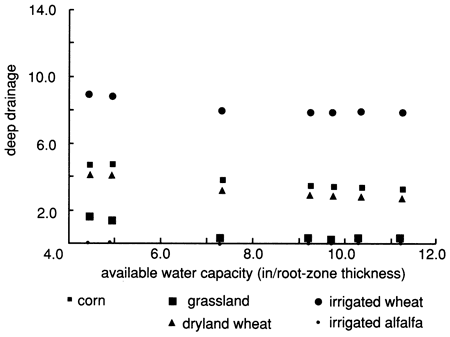
The highest deep drainage occurred in irrigated wheat fields, mainly because of the shallow rooting depth of wheat, while the lowest deep-drainage values occurred in alfalfa and grassland acreages (fig. 27). Interestingly, decreased amounts of deep drainage in the lower-precipitation northeastern portion of the watershed (fig. 23) are from grasslands, indicating the dominant effect precipitation and vegetation exert on deep drainage.
Figure 27--Effects of vegetation on deep drainage in Hudson climatic region of Rattlesnake watershed.
The scatter of points in all the above graphs is due to precipitation and temperature variations in the central and southwest portions of the watershed from which these data were derived.
Temporal Distributions of Climatic and Hydrologic Variables
The time distribution of important climatic and hydrologic components (maximum and minimum air temperature, precipitation plus irrigation, soil-moisture deficit of the root zone, deep drainage and runoff, as well as cumulative values of potential and actual evapotranspiration and precipitation plus irrigation) are graphically presented for selected plant covers growing in a "typical" soil association from the central portion of the watershed (figs. 28-31). Compare, for example, the dryland wheat-fallow sequence with the prairie grassland which possesses the deeper rooting system (figs. 28 and 29). Note the lower deep drainage and higher soil-moisture deficit in grasslands compared to wheat. Also compare the different characteristics of irrigated wheat-sorghum sequence with those of irrigated alfalfa (figs. 30 and 31), where in fact AE exceeds the VB-calculated PE most of the time, the minimal amounts of deep drainage in alfalfa, and the higher soil-moisture deficit compared to that of wheat (of course keep in mind the shallower rooting depths of wheat). Also note that additional irrigation during the summer months for sorghum contributed practically nil for deep drainage. From all these figures, the timing of deep drainage events can be concluded to occur during spring. The high water consumption of grasslands, as reflected by their high crop coefficients, reduces deep-drainage amounts during spring when most deep drainage occurs, in comparison to other crops.
Figure 28--Time patterns of water-balance components for dryland wheat-fallow rotation in Rattlesnake watershed.
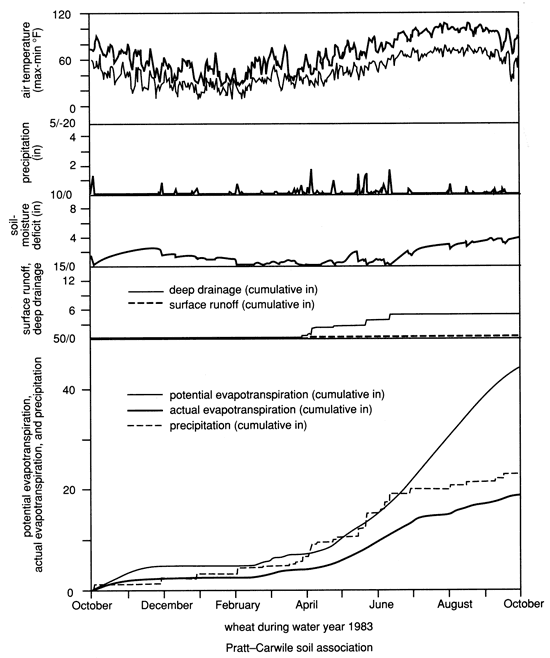
Figure 29--Time patterns of water-balance components for natural growth in Rattlesnake watershed.
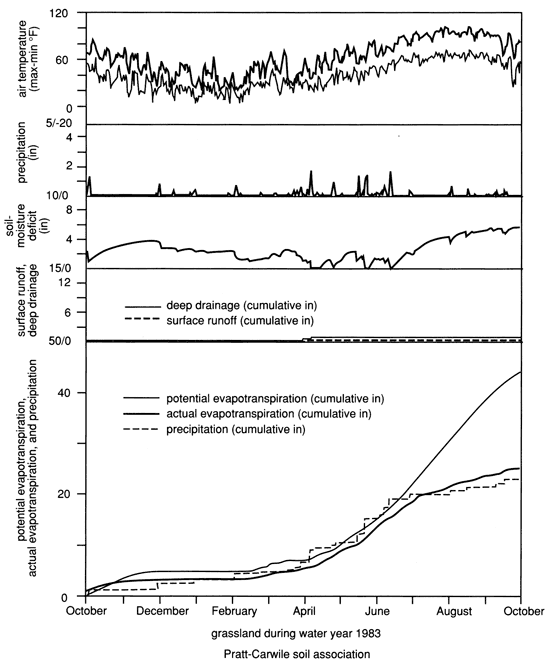
Figure 30--Time patterns of water-balance components for irrigated wheat-sorghum rotation in Rattlesnake watershed.
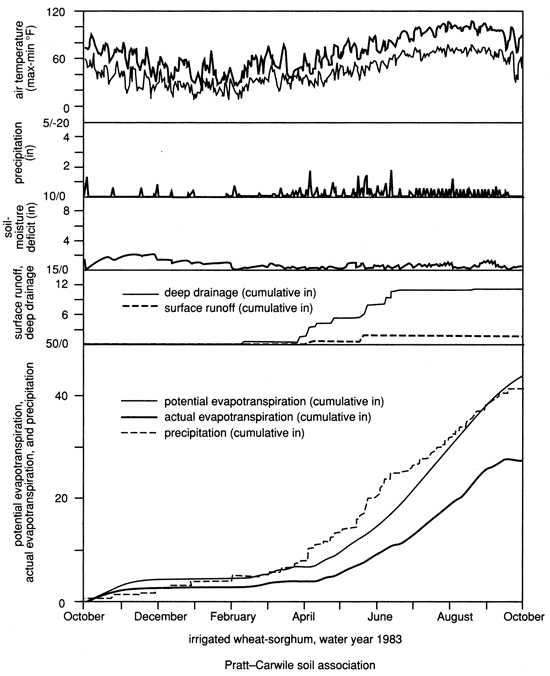
Figure 31--Time patterns of water-balance componenets for irrigated alfalfa in Rattlesnake watershed.
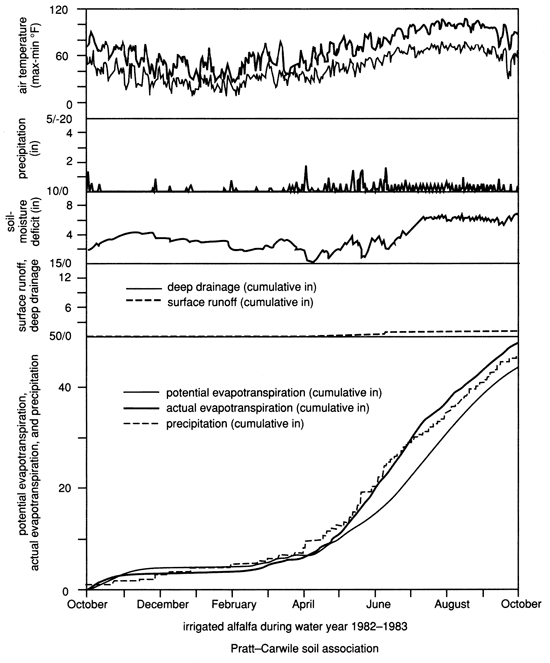
Areal Distribution of Hydrologic Variables
Information on the distribution of deep drainage, evapotranspiration, and runoff over the entire Rattlesnake watershed resulting from the methodology adopted in this study is shown in figs. 32-34, respectively. The same, and additional, information also is tabulated in appendix III, which indicates the amounts, in inches, of the hydrologic variables mentioned above, separated by hydroclimatic region, vegetation cover, and soil association. Appendix IV tabulates the amounts of the above-mentioned hydrologic variables in acre-feet as a function of hydroclimatic zone, soil association, and vegetation cover-land use. Figures 32-34 represent pictorial views of the complex spatial variation of the hydrologic parameters. The specific values from these maps can be found in appendix V, where the values of the various hydrologic variables, in inches, are compiled according to irrigated crops, nonirrigated crops, and natural growth, all as functions of soil and hydroclimatic complexes.
The areal distribution of deep drainage and thus potential ground-water recharge, is indicated in fig. 32. The highest drainage values (6 to approximately 8.5 inches [15.2-21.6 cm]) occur in the south-central portion of the watershed. This high distribution was the result of the combination of low soil-moisture capacity of the Pratt-Tivoli and Pratt-Attica-Carwile soil associations (see table 1), the high irrigation, and relatively high precipitation in the lower two-thirds of the watershed (compared to the northeastern portion of the watershed). The high deep-drainage region also coincides with the high soil-permeability region of the watershed (fig. 14). This high deep-drainage region is corroborated by the fact that no water-level declines (in fact, water-level rises) have been observed in this area since the 1940's; water-level declines have been observed in most other locations in the watershed (fig. 8). Note, however, that the water table in this high deep-drainage area is generally of the order of 50-100 ft (15-30 m) below land surface (fig. 7), and the deep drainage indicated by fig. 32 is from the bottom of the soil profile, normally 5 ft (~1.5 m) deep. The drainage figures in this case should be considered as indicating maximum or potential recharge under 1982-83 climatic and land-use conditions because of the likelihood of additional water losses. These losses can be due to (1) deeper-rooted plant usage; (2) subsurface lateral water movement due to thick clay layers which may redirect the downward soil-water flow laterally away from the input area and eventually toward the surface farther away; or (3) the absorption by the available water-storage capacity of the deeper unsaturated zone.
Figure 32--Areal-distribution map of deep drainage.
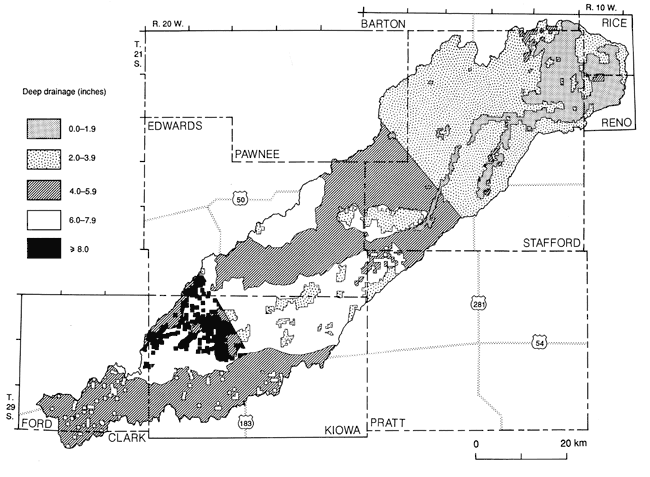
The smallest deep-drainage values (in the range of 0-2 inches [0-5 cm]) occurred in the northeastern portion of the watershed because a significant portion is natural grassland (which possesses a deep rooting system and a long active life cycle) with no significant irrigation development, relatively high moisture-capacity soils, such as the Natrustolls-Plevna soil association, and lower precipitation compared to the upper (southwestern) two thirds of the watershed for the water-accounting period. Deep-drainage values in this area likely correspond to the actual ground-water recharge because the depth to the water table is generally shallow, in the range of 10-20 ft (3-6 m).
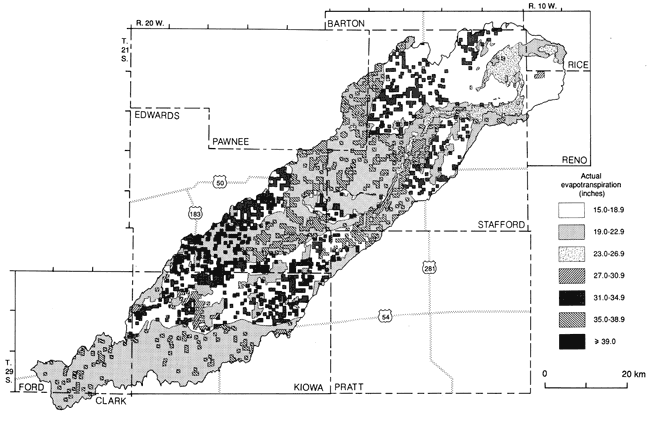
The distribution of actual evapotranspiration water loss is shown in fig. 33. Actual evapotranspiration is a complex function of climatic variables as reflected in the PE calculations, soil-moisture and soil-water capacity, Z table, and k coefficients. The highest evapotranspiration losses are easily recognized to occur in combinations of high-moisture-capacity soils and irrigated crops, while the lowest evapotranspiration losses occur in nonirrigated cropland and low-soil-moisture-capacity areas.
Figure 33--Areal-distribution map of actual evapotranspiration.
The distribution of surface runoff is shown in fig. 34. Runoff is greatly affected by the amount, intensity, and frequency of precipitation, in addition to geomorphological factors. In the Greensburg-Bucklin climatic region, where the intensity and frequency of rainfall were higher than in other portions of the watershed (fig. 18), the largest surface runoff values of 1 inch or higher are observed. Also note that this region is mostly covered with dryland wheat with a shallow rooting depth, which also contributes to higher runoff values given the appropriate precipitation conditions.
Figure 34--Areal-distribution map of surface runoff.
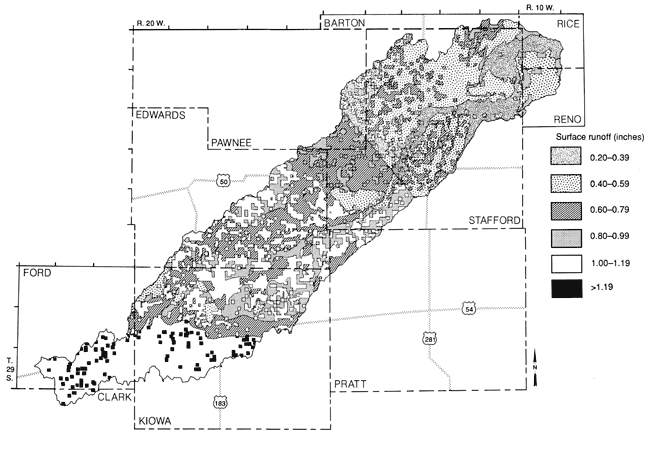
The lowest runoff values (0.2-0.5 inches [0.5-1.3 cm]) occur in the northeast portion of the watershed, which is covered to a large extent by grassland (with deeper rooting depths), nonirrigated crops, and relatively high soil-moisture capacities in combination with relatively low precipitation.
In general, the effect of irrigation is to significantly increase evapotranspiration and also increase deep drainage, as can be seen in figs. 20 and 21. For summer crops, such as sorghum and soybeans, as well as alfalfa, most of the irrigation amounts are spent in evapotranspiration activities, with negligible amounts for deep drainage. The effects of grasslands are reduced deep drainage and runoff and increased soil-moisture deficits compared to cropland acreages (figs. 19, 20, and 21). From the areal distribution of the various components of the water balance, we can conclude that single average values of hydrologic variables used in management practices are not realistic and that a spatial-discrimination attempt in managing water resources is needed.
Demonstration and Predictive Capabilities
A computerized water-balance procedure can be used to predict human and natural impacts on the hydrologic cycle. The hydrologic effects of vegetation changes, weather modification, extreme weather conditions, and so on can be readily estimated during the planning process. Thus, had the Rattlesnake watershed been entirely covered by prairie grasses, as it probably was during predevelopment time, and had the 1982-83 precipitation pattern and amount prevailed, the overall watershed deep drainage would have been 1.13 inches (2.87 cm), compared to 0.15 inches (0.38 cm) if alfalfa were planted exclusively in the watershed. If the entire watershed were planted with dryland wheat under 1982-83 precipitation conditions, the overall watershed deep drainage would have been 5.1 inches (12.9 cm). Such figures can be arrived at by multiplying the deep-drainage amounts for the corresponding crop and soil complex (appendix III) by the planted area (appendix IV), summing these figures, and dividing by the area of interest (appendix VI). Similarly the hydrologic effects of manipulating the proportion of various crops and the amounts of irrigation within any soil-association area can thus be assessed.
Provided that future precipitation patterns can be established, then, under known vegetation and land-use practices, various components of the water balance, such as deep drainage and surface runoff, can be readily predicted within the watershed using the presented methodology. An example of the relative effects of an ~19% precipitation difference on the components of the water balance, keeping the precipitation time-pattern constant, is shown in fig. 23. This figure represents actual grassland data from the northeastern watershed area, which received 18.9 inches (48.0 cm) of precipitation, and the rest of the watershed, which received an average of 23.3 inches (59.2 cm). Note the large increase in deep drainage in the higher precipitation region, especially in low-AWC soils, compared to the deep drainage in the lower precipitation region.
Some Assumptions and Limitations
Many assumptions are inherent in the simplification of complex problems such as simulating the water balance of the Rattlesnake watershed. The most important variables contributing to the water budget are believed to be accounted for in this study, and the various assumptions and simplifications made are believed to contribute only minor errors in comparison to the scale and totality of the problem. In addition to the simplifications and assumptions already mentioned in the "Versatile soil-moisture budget" section and in the irrigation and basinwide integration methodology subsections of the "Hydrologic budget implementation and synthesis" section, the following main assumptions also are made, or expanded here.
The rooting depths of most crops do not exceed 5 ft (1.5 m) because most soil descriptions in Soil Conservation Survey soil manuals do not extend beyond that depth. The largest error from this assumption would probably be for alfalfa, which may have roots extending to more than double that depth. A 5-ft (1.5-m) rooting depth for alfalfa underestimates AE and in high-precipitation areas may overestimate deep drainage. However, alfalfa represents only 5.1% of the watershed vegetation cover. Even at the modeled rooting depth of 5 ft (1.5 m), alfalfa is extremely efficient in extracting most of the available-moisture capacity of the soil profile, thus leaving negligible amounts to drain below the modeled root zone. Only AE would be appreciably affected by the small rooting depth, the error being limited to the additional available-water capacity of the deeper soil profile.
In the calculations presented here, the basic soil unit is the soil series (soil type) and not the soil association. The various soils are modeled separately and the budget parameters are subsequently averaged into soil-association budget parameters. The assumption is that the soils, as modeled, are not affected by surrounding soil series. This assumption is due to the nature of the VB procedure, which can model only one soil type, one vegetative type, and one hydroclimatic regime at a time. The water budget calculates hydrologic variables in units of length over an unspecified area, which needs to be estimated and integrated separately.
We reiterate here that the water-balance results presented are for an integrated system. For example, the water-balance parameters are calculated in relation to each other, but only within a particular soil type-vegetative cover complex. The soil combinations are all calculated separately and then merged together as areal averages. Similarly, the crop rotations are calculated separately and merged together to complete a full year, as explained in appendix I.
Natural growth or grassland and pastureland are considered to be equivalent and are represented by brome grass. Because the natural state of the basin is prairie and the wooded areas are minimal, no significant problems are anticipated with this assumption.
The Z table chosen for the basin (curve F, fig. 16) simulates sandy soils, thus providing an index to soil hydraulic conductivity. Soils with significant clay content would not release water as readily as sandy soils with the consequence that AE would be lower.
Variations in topographic elevation across the watershed are not explicitly considered in this VB procedure. This is particularly troublesome in noncontributing watershed areas for surface runoff. The resulting VB runoff estimates from noncontributing areas are not taken into account assuming, based on actual observations, that the excess-water puddles created eventually become part of the evapotranspiration process. However, because the basin is flatland, the disadvantage of ignoring surface slope in the VB may not be significant.
Deep drainage below the modeled root zone is assumed to eventually be incorporated into the water table. As mentioned previously, this may be a reasonable assumption in cases of relatively shallow water table. However, drainage restrictions due to very shallow water-table areas are not considered; here the water may not be able to drain below the rooting depth. This limitation may affect areas very close to flowing stream courses and marshlands.
Prev Page--Approach and Versatile soil moisture budget || Next Page--Verification, Conclusions
Kansas Geological Survey, Geohydrology
Placed on web Aug. 16, 2010; originally published 1990.
Comments to webadmin@kgs.ku.edu
The URL for this page is http://www.kgs.ku.edu/Publications/Bulletins/GW11/05_disc.html