Prev Page--Hydrogeologic Environment || Next Page--Implementation, Results
Approach
Water Budget
The hydrologic equation or water balance is basically a statement of the law of conservation of mass as applied to the hydrologic cycle. It states that in a specified period of time all water entering a specified area must either go into storage within its boundaries, be consumed therein, be exported therefrom, or flow out either on the surface or underground (Brown et al., 1972).
The water-balance method allows the planner to compute a continuous record of soil moisture, actual evapotranspiration, ground-water recharge, and surface runoff from a meteorological record, as well as some observations on the soil and vegetation.
The power of such a technique in planning is obvious. The water balance has been used to compute seasonal and geographic patterns of irrigation demand, the soil-moisture stress under which crops and natural vegetation can survive, the prediction of streamflow and water-table elevations, the flux of water to lakes, and variations of water level and salinity. The most obvious use of the water balance is in a basic description of the hydrology of a place or region. Maps can be drawn of the annual extreme water deficit or surplus or of the total annual irrigation need or ground-water runoff. Spatial patterns within a region or a large river basin can be employed in planning the distribution of resources.
The water balance also is useful for predicting human impacts on the hydrologic cycle. The hydrologic effects of weather modification or changes of vegetation cover can be quickly estimated at a very early stage in planning. The water balance is, therefore, a valuable tool in the analysis of water problems in a region.
The occurrence and distribution of soil water is a complex and integral part of any hydrological water balance. Whether the emphasis is on surface runoff, streamflow, evapotranspiration, or ground water, soil water plays a dominant role. The infiltration and evapotranspiration processes, in particular, are strongly related to the time-depth status of the soil-water profile. Most ground-water recharge occurs only after the soil profile becomes significantly wetted. Crop production also is highly dependent on the presence of adequate available soil water throughout the growing season.
Regionalizing Point Values
Most direct measurements of hydrologic variables, such as soil moisture and ground-water recharge, provide only point readings and do not integrate such variables in relation to space and time. Unlike common climatological observations, comparable soil-moisture or ground-water-recharge measurements using standardized techniques are rarely available on a network basis. With the exception of runoff, which is an integrated measurement, the problem of areal representation of point measurements of the water-balance elements exists. The high variations of site characteristics and of physical and physiological properties of plants lead to large water-balance differences in vegetated surfaces.
"Classification methods," whereby homogeneous hydrologic-unit areas are identified within the heterogeneous structure of a watershed, can be applied to generalize and regionalize site values of the water-balance elements throughout the whole watershed (Dyck, 1985). Parameter sets can be determined for each unit area taking into account the close coincidence of geomorphological-, soil-, and vegetation-distribution patterns. A basic matrix of site-factor complexes can be established for the subdivision of a watershed into unit areas. For the Rattlesnake Creek watershed these include local climate, main forms of land use, types of soil classes, and vegetation types.
"Meteorological methods" for estimating components of the hydrologic balance from weather data also have been proposed in order to overcome difficulties encountered with point measurements (Baier and Robertson, 1966). Because these budgeting techniques keep track of changes of various hydrologic components of the water balance by using standard meteorologic observations together with some soil and vegetation information, they satisfy to some extent the need for a space-time integrating technique.
Basinwide Integrating Methodology
In this study we combine aspects of the "classification method" with the "meteorological method" in order to derive a basinwide integration methodology. First the basin is divided into climatic subregions using a Thiessen-type polygon technique. Such a method seems appropriate because the study area is generally a flatland plain. The different soil series within each climatic subregion are then grouped into soil associations of similar soil properties using standard Soil Conservation Service techniques (U.S. Department of Agriculture, 1975). Each soil association is further subdivided according to land usage into irrigated cropland, nonirrigated cropland, and rangeland or grassland. This classification seems appropriate because our study area is predominantly agricultural, without any forested areas. Finally, a crop-rotation practice is superimposed on the land usage. We superimposed a meteorological water-budgeting procedure on this classification scheme, which is repeatedly run for each soil series, crop type, land-use practice, and climatic region. In order to avoid the averaging effects of monthly or other large time intervals on the water-balance components, daily input data were adopted in this study. Area-weighted averages were then taken for integrating the soil-plant-weather complexes on a watershed scale.
The described approach is intuitive and simple. The water-budgeting procedure, as will be explained in the next section, is not very involved, requires minimal data, and therefore is inexpensive to run. Therein lies the advantage of the proposed integrating technique.
Versatile Soil-Moisture Budget
Introduction
Most water-budgeting techniques make use of the well-known concept of potential evapotranspiration as an indicator of the possible maximum loss of water from the soil under conditions where soil-water supply is not limiting. Penman (1963) reviewed the extensive literature pertaining to moisture loss under conditions of nonlimiting water supply. Budgeting methods for estimating soil moisture and actual evapotranspiration from vegetated soil, when water supply is at times limited, are comparatively more complicated, because they account for various soil and plant characteristics that modulate or alter the potential rate. In this report a meteorological soil-moisture budget called "Versatile Budget," which is a multigeneration evolution of the Holmes and Robertson (1959) modulated budget, is employed.
The Versatile Soil-Moisture Budget (VB) requires as minimum input only daily observed data on precipitation and estimates of potential evapotranspiration (PE). The VB computerized procedure simulates variations in daily soil-moisture content by making use of physical and biological concepts of water movement in the soil and water uptake by plant roots (Baier et al., 1976). The VB output contains daily estimates of actual evapotranspiration (AE), soil-moisture content in several "zones" or layers in the soil profile, and water losses due to runoff and drainage. Because the data from climatological stations usually are considered to be representative of the surrounding area, we can assume that the soil-moisture estimates based on such data also are representative of the soil within this same area.
The basic structure of the budget can be described by the flow chart presented by Baier et al. (1979) shown in fig. 15. Model components can be split into evaporation functions, including all crop and soil-water extraction characteristics, and recharge functions including infiltration, drainage, runoff, and snowpack submodels.
Figure 15--Versatile budget flow chart (from Baier et al., 1979).
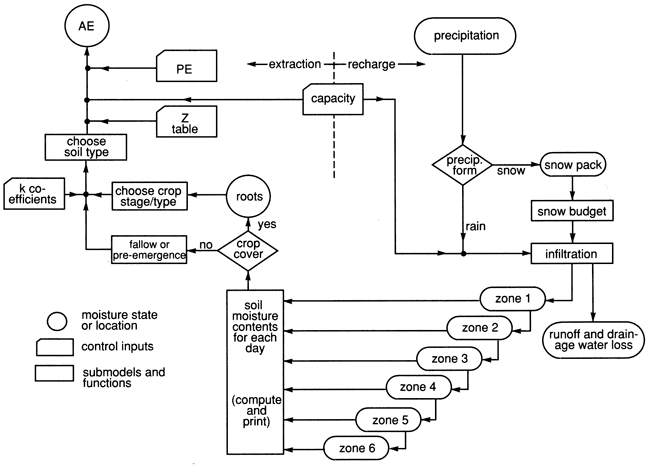
Evapotranspiration
As mentioned previously, daily values of precipitation and PE are required as input to the VB. A variety of techniques may be used to obtain the most reliable daily PE estimates under the local experimental conditions. For the daily calculations of PE from standard climatic data, Thornthwaite's method (Thornthwaite, 1948; Thornthwaite and Mather, 1955), which is mainly based on mean air temperature, was found to be inadequate (Ritjema, 1965). Penman's method (Penman, 1948), which generally is regarded as the most sound, requires observations on vapor pressure, wind, radiation or sunshine, and temperature; these data for a given station are often incomplete or not at all available. All other methods for estimating PE either involve special measurements or empirical coefficients of limited regional applicability or are not flexible enough to make efficient use of those meteorological factors that are available for a certain location and time period.
To overcome these shortcomings, Baier and Robertson (1965) proposed a regression technique for estimating daily latent-evaporation rates which can readily be converted to PE, using the standard climatic data that are available. Minimum input-data requirements are daily maximum and minimum temperatures available from various weather stations, and total sky and solar radiation at the top of the atmosphere (Q0) available from standard tables (Russelo et al., 1974). The latter is used to evaluate the solar radiation incident upon the earth's surface from easily observable or measurable quantities (Baier and Robertson, 1965). If in addition to the above data, daily values of sunshine, wind, and dew-point temperatures are available, the inclusion of any one or all of these variables in different regression equations usually improves the PE estimates. This method has been used for estimating daily or monthly PE values at different locations in Canada; these estimates were compared with actual observations or estimates from Penman's formula with good reported agreement (Baier and Robertson, 1965; Baier, 1967).
In the VB, water is withdrawn simultaneously from different depths of the soil profile in relation to the rate of PE, rooting patterns of crops, different soil-moisture-release characteristics, and the available water in each of several (usually six) zones of specified water-holding capacities. PE is used as a climatic parameter of the potential (maximum) rate of evapotranspiration from a dense crop freely supplied with water. Adjustments for runoff, drainage, different soil-moisture-release characteristics for upper and lower zones, and the relative effect of the daily atmospheric demand rate on the AE:PE ratio as a function of available soil moisture also are incorporated. The general equation of the VB for estimating daily AE from PE is

where AE is the daily actual evapotranspiration, PE is the daily potential evapotranspiration, Zj is the value from a selected soil-drying curve for the jth zone, kji is the crop coefficient for root extraction in the jth zone and ith crop-growth stage, Sj is the plant-available water for the jth zone at the start of the day, and Cj is the plant-available water capacity for the jth zone.
For the purpose of this budget, plant-available soil moisture is considered to be the total amount of moisture from field capacity to permanent wilting point. The concepts of field capacity and available water capacity have been helpful in the development of improved water-management practices because of their simplicity, despite the fact that field capacity is not a precise term.
The basic concepts of soil-moisture extraction in the VB follow (Baier, 1967):
- The total soil moisture available to plants is subdivided into six arbitrary "standard zones" of varying water-holding capacities, although a different number of zones also can be used (Dyer and Baier, 1980). Specifically, the six standard zones contain 5.0, 7.5, 12.5, 25.0, 25.0, and 25.0% respectively, of the total capacity for plant-available moisture of the soil profile. The adoption of "standard zones" made it possible to use one set of crop (plant or root) coefficients, k, for a particular crop in any type of soil. This is possible because it is assumed that the uptake of available water by crops always follows a characteristic pattern that depends on plant-rooting habits. Although the extent of the root system may differ from soil to soil, the fraction of the available water extracted from the different zones remains the same under various environmental conditions. Studies of rooting characteristics and extraction patterns by various researchers support this assumption (Vazquez and Taylor, 1958; Weaver, 1926).
- Water is taken up by plants at a rate depending on the ratio of available water present in any zone to the capacity for available water in the same zone.
- This rate is modified by
- the relationship between AE/PE and available water in the particular soil. This relationship is expressed by the adjustment factor Z which characterizes different types of soil-dryness curves. The Z factor is selected according to moisture characteristics of the soil;
- the crop (plant) coefficient, k, which resembles the most probable moisture-extraction pattern according to rooting characteristics and water consumption of plants at their different development stages.
As the soil dries, it becomes increasingly difficult for additional water to be lost by evaporation and transpiration. Different investigators have suggested that the shape of the curve of decreasing evapotranspiration with soil-moisture storage can be either concave or convex. These relationships also have been shown to be controlled by soil properties, particularly texture (Baier, 1968; Salter and Williams, 1965). Baier and Robertson (1966) and Baier (1968, 1969) have combined the various proposals for the relation between AE/PE under different values of soil-moisture content in the form of Z tables, which are presented in graphical form in fig. 16. Descriptions of available Z tables and some guidelines for their selection and use are given in Baier et al. (1979). An index equation for generalizing drying curves was developed by Dyer and Baier (1979).
The k coefficient expresses the amount of water (in percent of PE) that can be removed by plant roots from different soil layers during the growing season. To simulate this water uptake, the k coefficients change during the growing season according to crop-developing stages. The transition dates between crop stages must be read into the program for each year.
The k coefficients employed in the VB have been determined by iterative comparisons between computed and measured soil moisture or were estimated so that extraction rates resemble the most probable crop-rooting pattern under the prevailing environmental conditions. Dyer and Dwyer (1982) suggested that observed root patterns could be a basis for development of new sets of k-coefficients for different crops. Tables of k coefficients for different crops and growth stages are given in Baier et al. (1979).
Runoff, Infiltration, and Drainage
To account for water losses through runoff, a simplified relationship between soil moisture in the top zone, daily-precipitation total, and runoff is included in the VB. On days with precipitation ≤1.0 inch, the total amount of precipitation is considered to infiltrate into the soil. On days with precipitation >1.0 inch, runoff is estimated from equation (2):
Runoffi = RRi - I (2)
where
I = 0.9177 + 1.811 lnRRi - 0.97 lnRRi (Sj/Cj) (3)
and
I = amount of water infiltrating into soil
RRi = rainfall, in inches, on day i
Sj = soil moisture in the jth zone on day preceding the rain day
Cj = available water capacity of the jth zone
and j = 1.
Equation (3), calculated from data by Linsley et al. (1949), was based on findings by several researchers that mainly the initial soil-moisture content and rainfall affected the rate of infiltration.
In the VB, we assumed that the water infiltrating into the soil would first bring the moisture content of the top zone to field capacity and that the remainder would infiltrate into the next zone and so forth, until either all infiltration water was used up or all zones were brought to capacity. Drainage is obtained on days when the precipitation exceeds the total of AE, runoff, and the sum of moisture deficits over all zones. Any surplus of water was then designated as drainage.
In estimating AE on days with measurable rainfall, we presumed that most evapotranspiration on day i took place first and at a rate depending on the soil-moisture content at the end of day i - 1, but that rainfall occurred later in the ith day. This assumption is based on the fact that rainfall over a land mass in summer is typically of a showery nature and usually associated with the formation of cumulus clouds, which reach their maximum in the afternoon after strong convection earlier in the day.
In climates where snow occurs, the computation of soil moisture includes the amount of water penetrating the soil from snow. A simple snow budget was developed for use in the VB with minimum additional data. The reader is referred to Baier et al. (1979, 1972) and Dyer and Mack (1984) for further details and additional features.
Prev Page--Hydrogeologic Environment || Next Page--Implementation, Results
Kansas Geological Survey, Geohydrology
Placed on web Aug. 16, 2010; originally published 1990.
Comments to webadmin@kgs.ku.edu
The URL for this page is http://www.kgs.ku.edu/Publications/Bulletins/GW11/04_appr.html