Prev Page--Introduction || Next Page--Water Table and Quantity
Physical Properties of Water-bearing Materials
Definitions and General Considerations
The rate of movement of ground water is conditioned by the size and shape of the interstices in the rocks and the difference in hydraulic gradient from one point to another. The permeability of a water-bearing material is its capacity for transmitting water under pressure. The coefficient of permeability may be expressed as the number of gallons of water a day, at 60° F., that is conducted laterally through each mile of the water-bearing bed under investigation (measured at right angles to the direction of flow), for each foot of thickness of the bed, and for each foot per mile of hydraulic gradient (Meinzer's coefficient; see Stearns, 1927, p. 148). The coefficient of transmissibility (Theis, 1935, p. 520) may be defined as the number of gallons of water a day, at the prevailing temperature, that is transmitted through each mile of the water-bearing bed under a hydraulic gradient of 1 foot to the mile; hence it is the average coefficient of permeability, as defined above, multiplied by the thickness of the aquifer and adjusted for temperature.
The specific yield of a water-bearing formation is defined as the ratio of (1) the volume of water which a saturated aquifer will yield by gravity to (2) its own volume (Meinzer, 1923, p. 28). The quantity of water that may be removed from storage in a saturated material depends upon the specific yield of the material. Permeability, transmissibility, and specific yield were determined for the alluvium of Neosho valley by methods based on pumping
Behavior of the Water Level Near a Pumped Well
The following discussion has been adapted for use in this report from similar discussions by L. K. Wenzel and other members of the Federal Geological Survey.
As soon as a pump begins discharging water from a well under water-table conditions, the water table in the vicinity of the well is lowered, thus establishing an hydraulic gradient toward it. The water table soon assumes a form comparable to that of an inverted cone, the well being at the apex. For a short time most of the water that is pumped from a well is derived by unwatering materials close to it. As pumping is continued, more of the formation is gradually unwatered and a gradient is established which transmits to the well approximately the amount of water that is being pumped, most of the water being derived from ever increasing distances from the well. Thus, the cone of depression continues to expand and the water table within the cone continues to decline gradually. The development of the cone of depression may be halted if water is added to the formation by natural or artificial recharge.
After the discharge of a well is stopped, water continues to percolate toward the well for a time because the hydraulic gradient is still in that direction, but instead of being discharged at the surface the water refills the well and the adjacent material that was unwatered by the pumping. As the formation near the well is gradually refilled, the hydraulic gradient is gradually decreased and the recovery of the water level in the well becomes progressively slower. At a considerable distance from the well, the water level may continue to lower for a time after pumping has been stopped because water continues to move toward the well. In time there is a general equalization of water levels over the entire area affected, and the water table tends to assume its original form, although it may remain temporarily or permanently somewhat lower than before water was withdrawn.
Pumping Test
A test well, 30.4 feet deep, was constructed in February, 1942, by the Layne-Western Company at the site of test hole 36, in the NE SE SW sec. 4, T. 32 S., R. 21 E. This location for the pumping test was chosen by Mr. J. A. Fulkman, of the architect-engineers. The well was gravel-packed to a diameter of 38 inches and the 10-inch casing was perforated throughout the lower 10 feet. The pump used was a Layne turbine. Seven observation wells were drilled nearby so that measurements of the depth to water could be obtained at different distances and in different directions from the pumped well before, during, and after the pumping test. The location of the observation wells and other pertinent data are given in table 1.
Table 1--Location, diameter, depth, and altitude of wells used in the pumping test
| Well number |
Diameter (inches |
Depth of well below masuring point (feet) |
Height of measuring point above land surface (feet) |
Altitude of measuring point (feet above sea level |
Altitude of static waer level (feet above sea level |
Distance and direction from pumped well (feet) |
|---|---|---|---|---|---|---|
| 1 | 38.0 | 31.7 | 1.3 | 825.2 | 818.03 | 0 |
| 1S | 1.25 | 30.5 | .5 | 825.8 | 818.05 | 50 south |
| 1N | 1.25 | 29.5 | .5 | 822.4 | 817.82 | 50 north |
| 1E | 1.25 | 31.5 | .5 | 826.9 | 819.45 | 100 east |
| 1W | 1.25 | 27.5 | .5 | 820.2 | 817.45 | 100 west |
| 2S | 1.25 | 32.5 | .5 | 826.4 | 818.15 | 150 south |
| 2N | 1.25 | 25.5 | .5 | 819.7 | 817.7 | 150 north |
| 3S | 1.25 | 25.5 | .5 | 824.6 | 817.6 | 350 south |
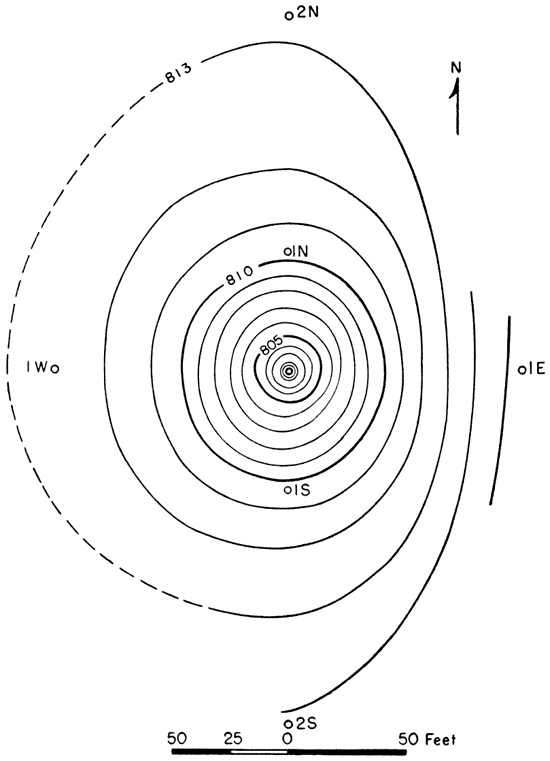
The well was pumped continuously for 98 hours at an average rate of 90 gallons a minute. The average pumping rate for the last 12 hours was 80 gallons a minute; at the end of the test the specific capacity (gallons a minute per foot of draw-down) was found to be 3.9. The water levels as measured in the pumped well and in the observation wells, and the pumping rates are given in table 2. Draw-down and recovery curves for the observation wells are shown in figure 4. The recovery curve for the pumped well is shown in figure 5. The shape of the water table near the pumped well at the end of the pumping test is shown in figure 6. The measurements of water levels were made by the wetted-tape method. The lower foot of a steel tape was coated with blue carpenter's chalk, so that the depth of immersion of the tape into the water could be seen plainly.
Fig. 4--Draw-down and recovery curves for the observation wells near the pumped well.
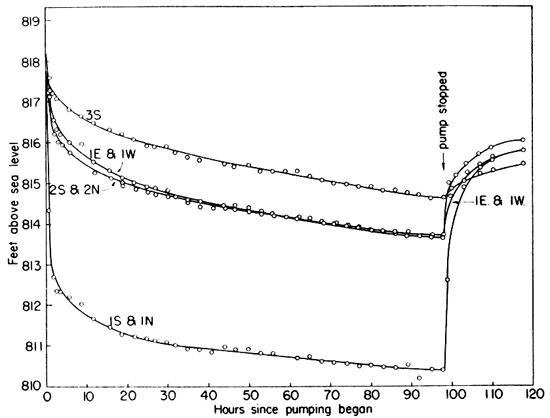
Fig. 5--Recovery curve for the pumped well.
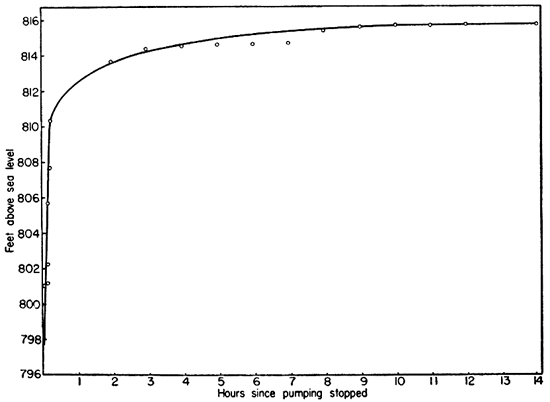
Fig. 6--Contour map of the water tale at the pumped well at the end of the pumping period. Contour interval 1 foot.
Determination of Permeability
The coefficient of permeability and the specific yield of water-bearing materials were determined in the field by methods described below. An attempt was made to determine in the laboratory the permeability of samples of gravel from the Neosho river valley, but the results obtained are believed to be in error, hence they are not included in this report. The samples collected from the test holes put down by the hydraulic-rotary method were washed in the field to free them of drilling mud, and no doubt much of the finer material also was washed away. Furthermore, some of the pebbles were too large to be used in the laboratory apparatus.
The data obtained from the pumping test (table 1 and table 2) were used in making determinations of the coefficient of permeability by the following methods.
Equilibrium Method
Thiem formula--The application of the Thiem formula for determining the permeability of water-bearing materials has been described fully by L. K. Wenzel (1936, pp. 1-26; 1942, p. 81). The method on which this formula is based consists of pumping a well that penetrates water-bearing material, the permeability of which is to be determined, and observing the decline of the water table or piezometric surface at several points around the pumped well. This formula is based on the assumption that the nonpumping water table is horizontal. Although this condition seldom exists, a horizontal water table may be assumed or a sloping water table may be corrected for and considered horizontal. The Thiem formula also involves the assumption that after approximate equilibrium is established around a pumped well, equal quantities of water move toward it in a given unit of time through successive concentric cylindrical cross sections around the well. Because the areas of the large cylinders through which the water percolates are greater than the areas of the smaller cylinders, the velocity of the ground water moving through. them is proportionately smaller.
According to Darcy's law (Darcy, 1856), the discharge through any concentric cylindrical section of water-bearing material, Q, is equal to the permeability of the material, P, multiplied by the hydraulic gradient, I, multiplied by the cross-sectional area, A. Hence, P = Q/IA. The hydraulic gradient at a given distance from the pumped well can be determined from the slope of the water table. For water-table conditions the area A is equal to 2π x (m-s); x being the distance from the pumped well; m the thickness of the saturated part of the water-bearing material; and s the draw-down at the distance x from the pumped well. The permeability of the water-bearing formation can be computed by substituting these values in the equation P = Q/IA. The method was first used by G. Thiem (1906), who developed a formula for computing permeability by using the draw-down as measured in two observation wells and the discharge of the pumped well rather than determining the flow through concentric cylindrical sections directly by Darcy's equation. Thiem's formula, modified for convenient use in the United States (Wenzel, 1936, p. 10), is
P = [527.7q log10 (a1/a)] / m (s-s1)
in which P = the coefficient of permeability as defined above,
q = rate of pumping in gallons a minute,
a and a1 = respective distances of two observation wells from the pumped well, in feet,
m (for water-table conditions) = average thickness (at a and a1) of the saturated part of the water-bearing bed, in feet,
s and s1 = draw-downs at the two observation wells, in feet.
From the data in table 2 and from distances indicated in figures 7 and 8, calculation of permeability by the Thiem method using wells located 50 and 150 feet from the pumped well follows:
q = 80 gallons a minute (average pumping rate for the last 12 hours of the test)
a = 50 feet (distance from well 1 to either 1N or 1S)
a1 = 150 feet (distance from well 1 to either 2N or 2S)
m = (dn + fo + jq +lr) / 4 = 17.9 feet
s = (ef + ij) / 2 = 7.6 feet
s1 = (cd + kl) / 2 = 4.3 feet
P = [527.7 x 80 x log10 (150/50)] / (17.9 X 3.3) = 341
Fig. 7--Cross section at the site of the pumping test showing location of observation wells, static water level, and cone of depression after 98 hours pumping.
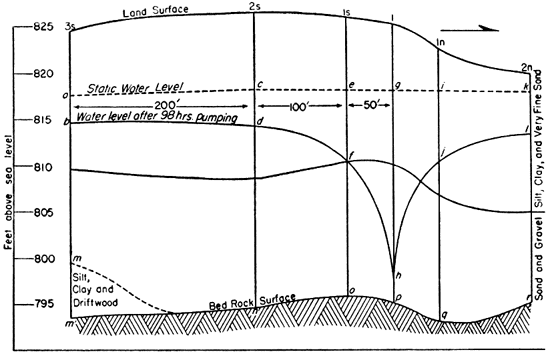
Fig. 8--Section at right angles to the section in figure 7.
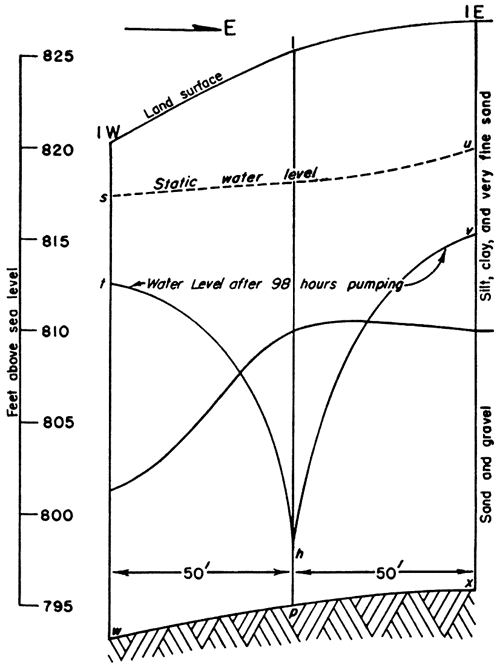
Table 3 gives the permeabilities obtained by using all combinations of observation wells along the north-south line (fig. 7). Wells 1E and 1W were not used in obtaining an average coefficient of permeability (fig. 8) because there was no other pair of wells located on the east-west line.
Table 3--Coefficients of permeability computed by the Thiem method (Pumping rate 80 g.p.m.).
| Distance from pumped well (feet) |
Average thickness of saturated part of water-bearing bed at a1 and a (feet) (symbol m) |
Average difference in draw-down at a and a1 (feet) (s - s1) |
Coefficient of Permeability (P) |
|
|---|---|---|---|---|
| Distant well (a1) |
Near well (a) |
|||
| 150 | 50 | 17.9 | 3.29 | 341 |
| 350 | 50 | 18.4 | 4.56 | 421 |
| 350 | 150 | 19.8 | 1.62 | 484 |
| Average | 415 | |||
As indicated in table 3, the values for the coefficient of permeability are increasingly greater when the draw-down in the more distant observation wells are used in the computations. The water-level measurements given in table 2 indicate that during the last 12 hours of pumping the rate of draw-down in the well 350 feet from the pumped well (3S) was greater than in the wells 50 feet distant (1N and 1S). These facts indicate that the cone of depression had not reached equilibrium form at distances 350 feet from the pumped well and that the value of 341 for the coefficient of permeability may be more nearly correct than the other values given in table 3.
Non-equilibrium Method
Theis recovery formula--C. V. Theis (1935) has shown that, under certain conditions, Darcy's law concerning the motion of ground water under natural conditions and under the artificial conditions set up by pumping is analogous to the flow of heat by conduction; hydraulic pressure being analogous to temperature, hydraulic gradient to thermal gradient, permeability to thermal conductivity, and specific yield to specific heat. From his final equation expressing the relation between the draw-down and the rate and duration of discharge of a well, Theis developed the following special formula for determining the transmissibility of an aquifer (as defined above):
T = (264q / s) x [ log10 (t / t1)]
in which T = coefficient of transmissibility
q = pumping rate, in gallons a minute
t = time since pumping began, in minutes
t1 = time since pumping stopped, in minutes
s = residual draw-down at the pumped well, in feet, at time t1
The Theis formula does not assume equilibrium conditions, as does the Thiem formula, and time is included as a factor. Residual draw-down (s) is computed by subtracting the static water-level measurement from appropriate depth to water-level measurements taken from the recovery curve (fig. 5). The proper ratio
[log10 (t / t1)] / s
is determined graphically by plotting log10 (t / t1) against corresponding values of s (fig. 9). Use of semi-logarithmic paper simplifies this procedure. For any convenient value for log10 (t / t1) the corresponding value for s may be found by inspection.
Fig. 9--Curve for pumping test obtained by plotting s against log10 (t / t1).
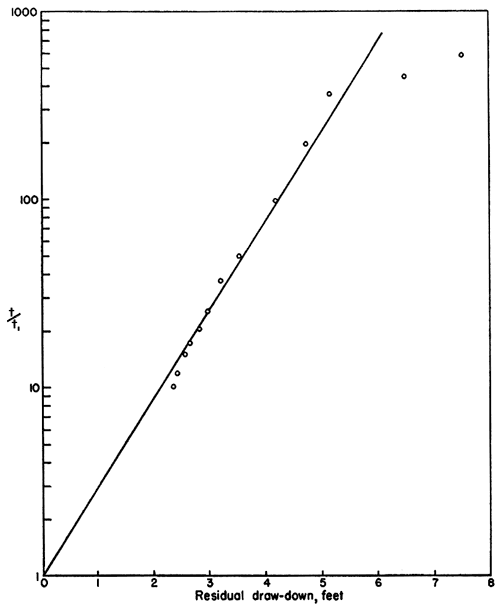
When values for s and t/t1 and q (80 gallons a minute) are substituted in the Theis recovery formula, the coefficient of transmissibility of the aquifer at the pumped well is computed to be 9,820. Dividing the coefficient of transmissibility by 23.1 feet, which is the average thickness of the saturated water-bearing material in the vicinity of the well, the coefficient of permeability is found to be 425, as compared with an average value of 415 computed by the Thiem method. [Note: As indicated in table 2, the temperature of the water during the pumping test ranged from 59° to 61° F., and averaged 60° F., hence no correction for temperature is needed.] As mentioned above, however, the minimum value for the coefficient of permeability (341) may be more nearly correct than the average value (415). On the other hand, the value of 425 obtained by using the Theis formula is in close agreement with the average value obtained by the Thiem method. The average of these two values, 420, is chosen as probably being the correct value. In other words, about 420 gallons of water a day are conducted laterally through each section of the aquifer 1 mile wide and 1 foot thick under an hydraulic gradient of 1 foot per mile.
Determination of Specific Yield
As Wenzel has shown (1936, pp. 53-57), the specific yield of a water-bearing formation can be determined by the pumping test method. When pumping begins in a well under water-table conditions, ground water is removed from storage in the vicinity of the well until eventually an hydraulic gradient that is essentially an equilibrium gradient is established and the quantity of water moving toward the well is equal to the rate of discharge of the well. Until conditions approaching equilibrium are reached, the quantities of water moving toward the well through successive concentric cylindrical sections of different diameter will not be the same as required by Darcy's law, but will differ by the differences in the quantities of water being removed from storage along each cylinder.
The specific yield may be determined by ascertaining the difference in the quantities of water that percolate through any two cylindrical sections in a given time, and may be expressed by the equation
y = 100 (Y1 - Y) / V
where y is the specific yield; Y1 is the quantity of ground water, in cubic feet, that percolates through the smaller cylinder; Y is the quantity of ground water, in cubic feet, that percolates through the larger cylinder; and V is the volume of water-bearing material, in cubic feet, that is unwatered between the two cylinders.
The volume of water-bearing material that is unwatered between concentric cylindrical sections around the pumped well may be computed by the formula
V = π(a2 -a12) (s + s1) / 2
in which V is the volume of unwatered material, in cubic feet; a is the radius of the large cylinder, in feet; a1 is the radius of the small cylinder, in feet; and s and s1 are the depths that the water table is lowered during the period, in feet, at the distances a and a1, respectively, from the pumped well.
The quantity of water that percolates through each cylinder may be computed by the formula y 2 PiahtY = (2 x Piaht) / (7.48 x 24)
in which Y is the quantity of ground water, in cubic feet; P is the coefficient of permeability; i is the average hydraulic gradient, in feet per foot, at the distance a from the pumped well; h is the average thickness, in feet, of the saturated water-bearing material at the distance a; and t is the period of pumping, in hours. Values of the specific yield determined by this method for several periods of pumping are given in the following table.Table 4--Values of specific yield (expressed as percentage) computed for cylindrical ections 100 and 300 feet in diameter for several different periods of pumping.
| Time | 6 hrs | 12 hrs. | 24 hrs. | 36 hrs. | 48 hrs. | 72 hrs. | 96 hrs. |
|---|---|---|---|---|---|---|---|
| Specific Yield | 1.2 | 3.7 | 5.4 | 7.7 | 10.3 | 16.7 | 19.5 |
As indicated in the above table, the computed value of the specific yield becomes larger as the period of pumping increases, because considerable time is required to drain the unwatered material completely. Plotting the computed values against pumping time suggests that the true specific yield of the material around the well is about 20 percent. In other words, each cubic foot of material that is completely drained yields about 0.20 cubic foot of water.
Prev Page--Introduction || Next Page--Water Table and Quantity
Kansas Geological Survey, Geology
Placed on web Aug. 11, 2008; originally published March 1944.
Comments to webadmin@kgs.ku.edu
The URL for this page is http://www.kgs.ku.edu/Publications/Bulletins/52_2/03_mater.html