This chapter is organized in three sections as follows. The Hydraulics Characteristics section presents a survey of the hydraulic characteristics of the river, examining a number of variables that affect water discharge and sediment load. The Changes in Morphology section reviews the morphological changes observed in the Kansas River over the last few decades, as a result of natural processes and human activities. The Impacts of Future Dredging section attempts to predict the impact of future dredging in segments of the river that have not had significant dredging activity.
Gregory C. Ohlmacher, Kansas Geological Survey
The Kansas River is a dynamic fluvial river system that transports sediments, erodes existing soil and rock, and creates new sediment deposits. The volume of sediments transported (sediment load) and the grain-size distribution of those sediments is controlled by the hydraulic parameters of the river channel including the supply of sediments, depth and width of the stream, cross sectional area and slope of the channel, and velocity and discharge of the water. Knowledge of these hydraulic characteristics is important for determining the effects of human activities on the river.
Channel Morphology
The Kansas River has been altering its valley and channel throughout its history. During Pleistocene times, multiple glacial events provided the meltwater and sediments to vertically erode a deep valley into bedrock and to widen this valley by lateral erosion. Since the Ice Age, the river has repeatedly filled this valley with sediments (aggraded) and eroded these sediments from the valley (degraded). Aggradation, degradation, and lateral erosion are controlled by the ability of the stream to move sediments, which in turn is controlled by the channel morphology, water velocity, and discharge.
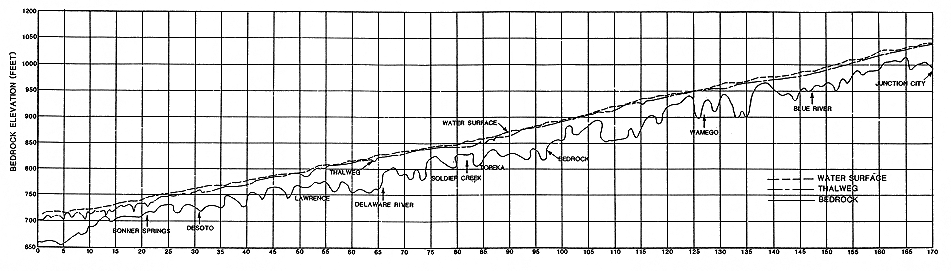
Several river features that are not related to water flow may affect aggradation/degradation and lateral erosion. The presence of shallow bedrock and coarse gravel deposits can prevent erosion in the river channel. Simons et al. (1984) noted shallow bedrock or bedrock exposed in the bottom of the channel at river mile (R.M.) 12-13, 101, and 132 (Figure 3.1). Cobbles, pebbles, and coarse gravel that cannot be moved by water flow can armor the bottom of the channel, preventing erosion. Simons et al. (1984) report gravel armoring at R.M. 9.7, 1213, 21.5, and 132. The Corps of Engineers reported armoring at R.M. 167 in 1956; however, Simons et al. did not find this deposit in 1984. Slack water areas along the river can be areas of aggradation. The water flow in the lowest reach of the Kansas River (R.M. 0 to R.M. 12.2) is controlled by the stage of the Missouri River and tends to be very slow. This reach has experienced some aggradation (Simons et al., 1984).
FIGURE 3.1--Bedrock, thalweg, and water-surface profiles for the Kansas River from Simons et al. (1984). A large version of this figure is available.
Several human-made features affect aggradation/degradation and lateral erosion. The Johnson County weir at R.M. 15.0 and Bowersock Dam at R.M. 51.7 affect erosion by preventing any degradation occurring on the downstream side of the structure from proceeding upstream. The slack water areas behind these structures provide localized areas of aggradation. Areas where riprap (large stones) has been placed and where jetties have been constructed will help prevent lateral erosion. Reservoirs on tributary streams and rivers also affect aggradation on the Kansas River by modifying the natural discharge patterns. By lowering the peak flood discharge, reservoirs lower the volume of sediment moved during a given flood. By increasing the daily discharge between floods, reservoirs may allow the stream to transport a higher quantity of fine-grained material. However, the latter effect is relatively minor. Other activities by humans that may have minor effects on aggradation/degradation include water withdrawn for municipal usage and irrigation, water pumped from alluvial aquifers, and municipal wastewater released into the river.
Three geomorphologic features important to the sediment and flow analyses are the thalweg, the topwidth, and the cross section. The thalweg is a line connecting the deepest parts of the channel. Plots of the thalweg (Figure 3.1) can be used to determine the local slope of the channel. The higher the slope, the greater the water forces acting on the sediments and the greater the volume of sediment that can be transported. Changes in the thalweg elevation with time can be used to monitor the amount of aggradation/degradation of the channel. This will be discussed later in this chapter.
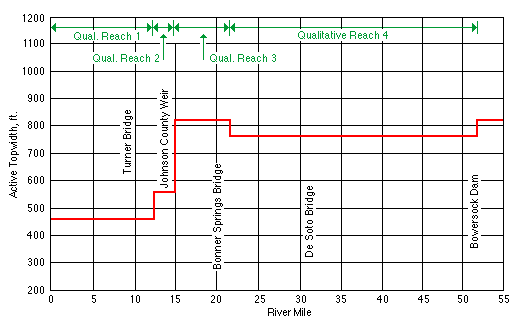
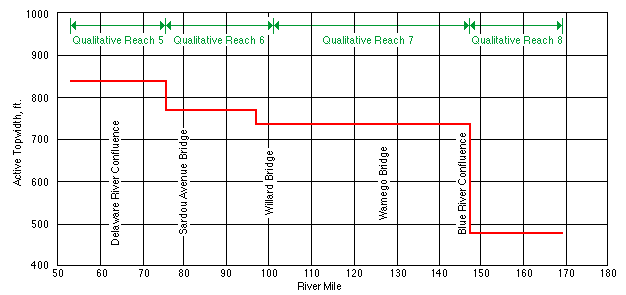
The topwidth is the horizontal distance between the stream banks at the top of the channel. It is a measure of the width of the river when the channel is bankfull. Simons et al. (1984) measured the topwidth along the length of the Kansas River (Figure 3.2), and combined these measurements with thalweg and sediment measurements to subdivide the river into reaches with similar properties. The reach-average topwidth of the Kansas River is about 480 feet (146 m) wide near the confluence of the Smoky Hill and Republican rivers. The reach-average topwidth increases downstream to a maximum width of 840 feet (256 m) near Perry. Between Perry and the Johnson County weir the topwidth fluctuates around 800 feet (244 m), and below the Johnson County weir the topwidth narrows to about 460 feet (140 m).
FIGURE 3.2--Average topwidth versus river mile from Simons et al. (1984).
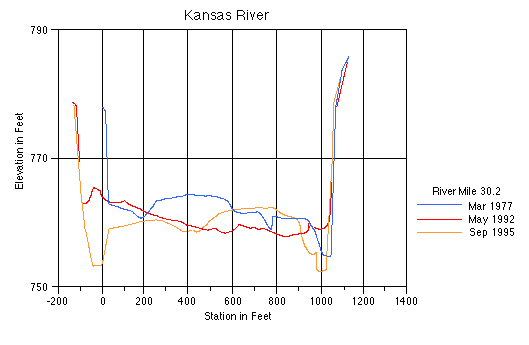
Channel cross sections are used to monitor changes in the channel morphology (thalweg and topwidth) and to calculate relationships between discharge and water depth. Channel cross sections are topographic profiles measured transverse to the flow direction. Figure 3.3 contains cross sections measured at R.M. 30.2, which is just downstream from the De Soto U.S. Geological Survey (USGS) gaging station (R.M. 31). These cross sections show that from 1977 to 1992, the river widened its channel, increasing the topwidth, and aggraded slightly. Between 1992 and 1995, the topwidth remained constant but the thalweg elevation decreased, indicating some degradation. Simons et al. (1984) document numerous changes in cross section of the Kansas River (Table 3.1). The use of cross sections to calculate depth-discharge relationships will be discussed later in this section.
FIGURE 3.3--Cross section of the Kansas River at R.M. 30.2 near De Soto, Kansas (from unpublished data U.S. Army Corps of Engineers).
Dredging may lead to changes in the morphology of the river. Dredging deepens the channel, increasing the slope of the channel upstream from the dredge. This could lead to degradation upstream of the dredge and widening of the topwidth by lateral erosion. The removal of sediment by the dredge locally traps some of the sediment being transported by the river. This could cause some degradation downstream of the dredge as the river erodes sediment deposits in order to restore its sediment-carrying capacity. The effects of dredging will be covered in greater detail in later portions of this chapter.
TABLE 3.1--Changes in cross section observed by Simons et al. (1984).
| River Mile | Period | D Channel Bottom | D Channel Width |
|---|---|---|---|
| 9.5 | 1962-1977 | No change in thalweg elevation, low-flow channel shifted | Slight narrowing |
| 13.68 | 1954-1983 | Main channel lowered 20 ft, little or no change from 1977 to 1983 | Widened approx. 150 ft |
| 14.10 | 1956-1977 | Thalweg lowered 12 ft, main channel lowered 7 ft | Slight narrowing of channel |
| 17.07 | 1977-1983 | No change, low-flow channel shifted | No change |
| 17.55 | 1954-1977 | NA* | Widened approx. 150 ft |
| 21.00 | 1956-1983 | Little change for 1956-1962, thalweg lowered 13 ft and main channel lowered approx. 8 ft from 1962 to 1977, thalweg raised 4 ft and main channel raised approx. 6 ft for 1977-1983 | Widened approx. 100 ft |
| 22.68 | 1977-1983 | Main channel lowered 3 ft, thalweg lowered 3 ft | Left bank widened approx. 100 ft |
| 23.17 | 1954-1977 | NA* | Right bank widened approx. 180 ft |
| 23.70 | 1962-1983 | No change, low-flow channel shifted to right bank | Left bank widened approx. 150 ft |
| 24.85 | 1977-1983 | More pronounced low-flow channel. Low-flow channel shifted, thalweg eroded 4 ft | Slight widening of channel |
| 26.91 | 1977-1983 | Average channel lowered 1-2 ft, low- flow channel shifted to left bank | Slight widening at left bank |
| 28.96 | 1977-1983 | Thalweg lowered 4 ft, low-flow channel shifted to left bank | Right bank widened approx. 25 ft |
| 31.04 | 1977-1983 | Thalweg lowered 7 ft; main channel aggraded 3 ft | No change |
| 61.4 | 1977-1979 | Thalweg lowered ~2 ft; minimal net degradation of channel | Bank widened approx. 100 ft |
| 62.5 | 1962-1979 | Thalweg lowered ~3 ft; net degradation ~2 ft | Left bank widened ~25 ft |
| 63.8 | 1962-1979 | Net degradation ~2 ft | Left bank widened ~15 ft |
| 63.9 | 1962-1979 | Thalweg lowered ~5 ft; main channel lowered 3 ft | No change |
| 68.2** | 1962-1979 | Main channel lowered 3 ft; thalweg, no change | Narrower by approx. 100 ft |
| 106.2** | 1962-1979 | No change | Widened by approx. 125 ft |
| 115.4 | 1962-1979 | No change in thalweg; more pronounced low-flow channel | Widened by approx. 70 ft |
Discharge Statistics
The Kansas River also features considerable variation in discharge related to climate, season, and location in the drainage basin. Discharge is a measure of the flow in a river and is defined as the volume of water that would pass through a cross section per unit time period. Throughout this chapter discharge will be given in cubic feet per second (ft3/s or cfs). The subsection is subdivided into discussions of temporal and areal variations in discharge.
Temporal variations in discharge--The effects of weather patterns on discharge are shown in plots of the monthly discharge (Figure 3.4). The Fort Riley (R.M. 170), Topeka (R.M. 83), and De Soto (R.M. 31) USGS gaging stations were chosen to represent the upper, middle, and lower reaches of the river, respectively. The 1993 flood and wet years in 1987 and 1995 show up as peaks; dry years, such as 1988, show up as valleys in Figure 3.4. During wet years, the river has an increased sediment load and the average transported grain size should be larger. However, the wet year peaks make up only a small percentage of the total time represented by the plot.
FIGURE 3.4--Stream hydrograph showing the monthly discharge plotted for water years 1987 to 1996 for Fort Riley, Topeka, and De Soto U.S. Geological Survey (USGS) gaging stations.
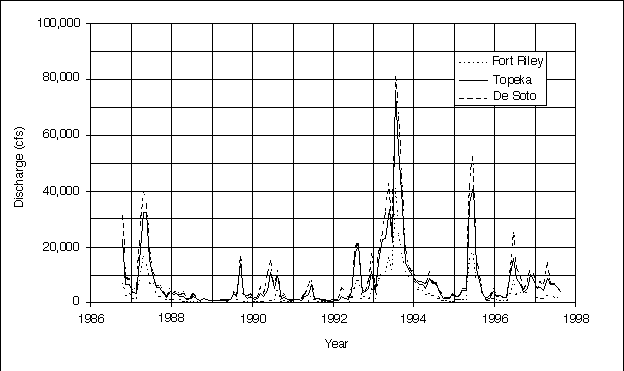
The response of the river to weather patterns appears to be fairly uniform throughout the valley. The peaks and valleys in Figure 3.4 occur roughly at the same time for the three stations. The magnitude of discharge depends on the location of the storm and the drainage area affected. The discharge is less upstream at the Fort Riley USGS gaging station where the drainage basin is smaller than it is downstream at the De Soto USGS gaging station where the drainage basin is larger.
The post-storm discharge response also is evident in Figure 3.4. After the storm peaks, the discharge rapidly declines as the overland runoff ends. Overland runoff is stormwater that travels over the ground surface to the river. The early period is followed by a period where the decline is much slower. During this later period, the discharge is supplied by ground water referred to as baseflow, and by water released from reservoirs on the tributary streams. Baseflow and reservoir releases can continue for several months to a year after a storm event. One can observe both the early and late periods of decline by examining the periods after the 1993 flood and the wet year in 1987 (Figure 3.4).
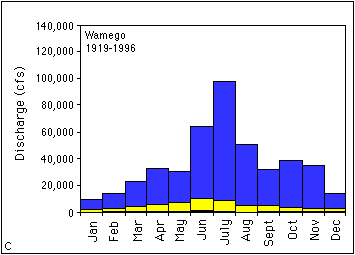
The peak discharges in Figure 3.4 occur during the middle months of the year. Figure 3.5 is a plot of the mean monthly discharge and compares how discharge changes with time of the year. The lowest flows are recorded during December and January (Table 3.2). The period from February to April shows an increase in discharge due to spring thaw and increasing precipitation. The months of May through July have the largest discharge. The discharge during August rapidly declines, as the weather becomes drier. Baseflow and water releases from the reservoirs supply discharge from September through November. No attempt was made to separate the portion of the discharge due to baseflow from that due to releases from reservoirs.
TABLE 3.2--Maximum and minimum mean monthly discharge (ft3/s).
| Month | Wamego (1919-1996) | Topeka (1917-1996) | De Soto (1917-1996) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Maximum | Mean | Minimum | Maximum | Mean | Minimum | Maximum | Mean | Minimum | |
| Jan. | 9,735 | 1,909 | 302 | 11,280 | 2,140 | 328 | 15,990 | 2,841 | 364 |
| Feb. | 14,320 | 3,086 | 494 | 16,720 | 3,421 | 500 | 20,800 | 4,436 | 635 |
| Mar. | 23,240 | 4,729 | 465 | 27,610 | 5,432 | 492 | 36,560 | 7,062 | 632 |
| Apr. | 32,710 | 5,813 | 606 | 32,500 | 6,819 | 650 | 43,570 | 9,356 | 845 |
| May | 30,610 | 7,541 | 379 | 36,010 | 8,657 | 585 | 43,270 | 11,139 | 953 |
| June | 64,620 | 10,807 | 1,114 | 64,670 | 11,972 | 1,075 | 78,870 | 15,233 | 1,188 |
| July | 98,420 | 9,155 | 747 | 109,100 | 9,926 | 986 | 133,200 | 11,949 | 1,106 |
| Aug. | 50,300 | 5,296 | 271 | 55,350 | 5,707 | 269 | 66,680 | 6,975 | 455 |
| Sept. | 32,530 | 5,011 | 388 | 34,840 | 5,437 | 425 | 44,660 | 6,751 | 525 |
| Oct. | 39,030 | 4,031 | 336 | 42,320 | 4,417 | 348 | 51,630 | 5,728 | 365 |
| Nov. | 35,430 | 2,785 | 390 | 35,190 | 3,130 | 406 | 42,320 | 4,255 | 504 |
| Dec. | 14,410 | 2,316 | 384 | 16,140 | 2,603 | 383 | 21,940 | 3,450 | 465 |
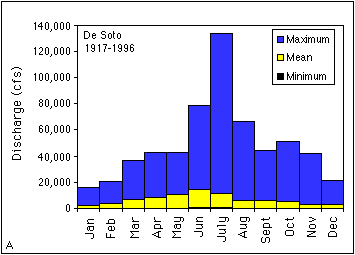
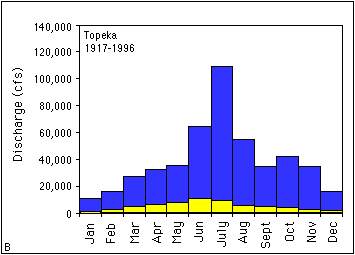
The plots in Figure 3. 5 show the overall trend in the data but not the variability for a given month. To demonstrate the variability in discharge, plots showing the maximum, minimum, and mean monthly discharge (Figure 3.6a-c) were generated from data in Table 3.2 for the De Soto, Topeka, and Wamego USGS gaging stations representing the lower, middle, and upper Kansas River, respectively. All three of these stations have sufficiently long periods of record from about 1920 to 1996 and can be used for comparison. The plots in Figure 3.6 demonstrate that the largest discharges are associated with the summer months and the smallest discharges are in the winter. It should be noted that the maximum monthly discharge for all three stations is in July rather than June as shown in Figure 3.5. These maximum monthly discharges reflect the peak discharges for the 1951 flood. Table 3.2 shows that the variability in discharges for the three stations can be up to two orders of magnitude (the maximum discharge is about 50 to 100 times larger than the minimum).
FIGURE 3.5--Plot of mean monthly discharge for the Fort Riley, Wamego, Topeka, and De Soto USGS gaging stations along the Kansas River.
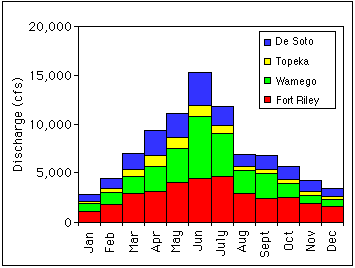
FIGURE 3.6--Plots showing maximum, minimum, and mean monthly discharge (ft3/s) for the (A) De Soto, (B) Topeka, and (C) Wamego USGS gaging stations.
Flow-duration curves (Figure 3.7) are used to rank the discharge. A flowduration curve rates the percentage of time (probability) that a discharge value is reached or exceeded. For example, a discharge value of 10,000 ft3/s is equaled or exceeded about 20% of the time for the De Soto area, but only 6% of the time near Fort Riley. This occurs because Fort Riley is located at R.M. 170, where the drainage basin is smaller and the climate is drier. The ranking of discharges is important to the analysis of sediment load and grain size. The larger the discharge, the larger the sediment load and the larger the grain size that can be moved.
FIGURE 3.7--Flow-duration curves for several of the Fort Riley, Wamego, Topeka, and De Soto USGS gaging stations along the Kansas River.
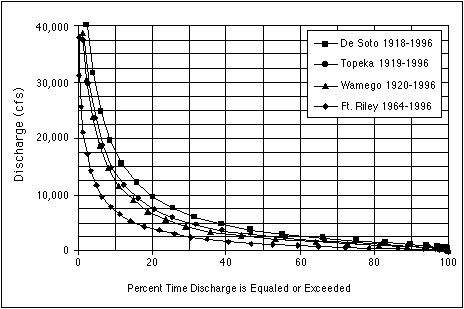
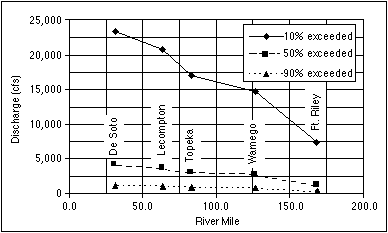
The recurrence interval, which is the average time in years between discharges of a certain value or higher, can be found by taking the inverse of the decimal value of the probability. Thus, a discharge with a 50% probability will have a recurrence interval of two years (1/0.5). For a probability of 50%, a two-year event, the discharge at Fort Riley would be 1,223 ft3/s, at Topeka would be 2,642 ft3/s, and at De Soto would be 3,346 ft3/s. For a probability of 10%, a 10-year event (flood), the discharges for Fort Riley, Topeka, and De Soto would be 7,221 ft3/s, 13,940 ft3/s, and 17,916 ft3/s, respectively. These values will be used later in this section to examine the sediment load and the maximum transportable grain size.
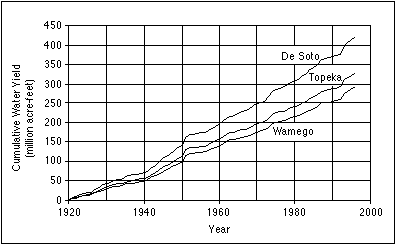
The cumulative water yield for the period from 1920 through 1996 is shown in Figure 3.8. Water yield is the total volume of water passing a point along a river. The values for water yield are in acre-feet, which is the volume of water required to cover an acre of land to a depth of 1 foot (0.3 m). Simons et al. (1984) observed an increase in the slopes of all the curves in Figure 3.8 beginning in about 1940. The slope of the curve represents the average annual water yield for the station. Table 3.3 contains the average annual water yields for 10-year periods beginning in 1920 and for the periods before and after 1940. Prior to 1940, the average annual water yield was 2,419,000 acre-feet for the Wamego USGS gaging station, 2,726,000 acre-feet in the Topeka USGS gaging station, and 3,479,000 acre-feet for the De Soto USGS gaging station. After 1940, the average annual water yield nearly doubles at all three USGS gaging stations. Simons et al. (1984) attribute the change in average annual water yield to a minor change in climate, although they point out that limited data exist for the period prior to 1940. The lower water yields for the period prior to 1940 include the drought years of the 1930's.
FIGURE 3.8--Cumulative water yield for the Wamego, Topeka, and De Soto USGS gaging stations.
Areal variations in dischargeThe general increase in discharge and the locations of major tributary input can be determined by examining plots of discharge along the river valley. Figure 3.9 is a schematic representation of the Kansas River showing the mean annual discharge and drainage basin area for the active and retired USGS gaging stations. As expected the discharge increases along the river valley with a couple of exceptions. The Belvue USGS gaging station (R.M. 115.4) has the highest annual discharge at 7,414 ft3/s because this is a fairly recent station and the data are strongly influenced by the 1993 flood. The Bonner Springs station (R.M. 20) has an annual discharge that is lower than the De Soto station (R.M. 31) because the Bonner Springs station was retired prior to the 1993 flood.
FIGURE 3.9--Schematic representation of the Kansas River updated from Simons et al. (1984).
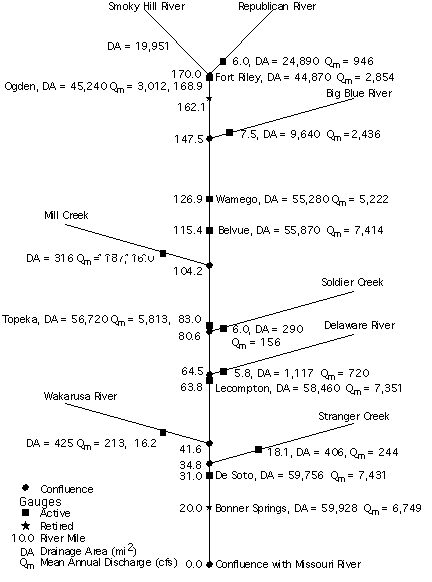
TABLE 3.3--Average annual water yield (millions of acre-feet).
| Years | Wamego | Topeka | De Soto |
|---|---|---|---|
| 1920-29 | 2.658 | 3.022 | 3.969 |
| 1930-39 | 2.179 | 2.430 | 2.988 |
| 1940-49 | 4.530 | 5.170 | 6.441 |
| 1950-59 | 4.223 | 4.600 | 5.579 |
| 1960-69 | 3.673 | 4.123 | 5.422 |
| 1970-79 | 3.991 | 4.514 | 6.023 |
| 1980-89 | 4.080 | 4.589 | 6.233 |
| 1920-39 | 2.419 | 2.726 | 3.479 |
| 1940-96 | 4.248 | 4.778 | 6.132 |
The distribution of extreme discharge values with river mile is plotted in Figure 3.10. The plot shows discharges that are exceeded 10%, 50%, and 90% of the time, which represent recurrence intervals of 10 years, two years, and about yearly, respectively. The data used for this plot are for water years 1967 through 1996 (October 1966-September 1996). The stations shown on the plot are the only ones that were active throughout the entire period. Regions of the plots where the slopes of the lines are steeper indicate reaches with increased input from tributary streams. Two particular examples are the reach between Fort Riley and Wamego and the one between Topeka and Lecompton. In the former the Big Blue River joins the Kansas River at Manhattan (R.M. 147.5), and for the latter reach the Delaware River enters the Kansas River at Perry (R.M. 64.5).
FIGURE 3.10--Plot showing the distribution of discharge along the Kansas River based on the USGS gaging stations that were active during water years 1967 to 1996.
Stage-discharge Relationships
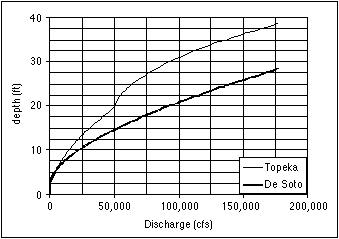
The discharge values must be converted into equivalent water depths in order to calculate the maximum grain size that can be transported. Knowledge of the maximum transportable grain size can be used to determine what reaches are armored by sediments too large to be transported. The relationship between water depth and discharge is established by developing a rating curve for the gaging station using the Manning equation. The Manning equation requires a cross section, the local slope of the channel, and a factor called the Manning number. Cross sections are available from the U.S. Army Corps of Engineers for the lower portion of the Kansas River. The slope of the channel can be determined using the thalweg profiles. The Manning number, which handles the unit conversion and accounts for the conditions along the channel, was found by comparing a number of rating curves with different Manning numbers with U.S. Geological Survey curves relating gage height to discharge. The Manning numbers selected compared favorably with published values for rivers similar to the Kansas River (Barnes, 1967). Figure 3.11 shows the rating curves developed for the De Soto and Topeka USGS gaging stations. Differences between the curves illustrate how changes in the cross section affect the relationship between depth and discharge. Note that cross sections at any given location vary with time, and thus the rating curves also vary with time. The rating curves in Figure 3.11 will be used to analyze the transportable grain size for different discharges at the two locations.
FIGURE 3.11--Synthetic rating curves for the Topeka and De Soto USGS gaging stations.
Sediment Transport
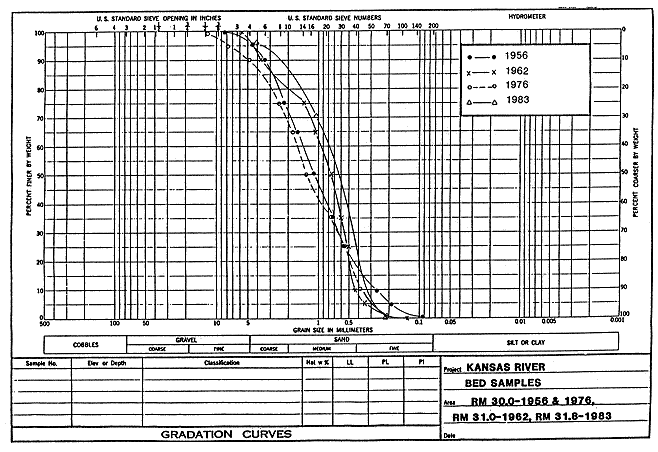
Sediments transported by streams are subdivided into three categories: wash load, suspended bed load, and bed load. Wash load is the finegrained material that is transported in suspension and almost never rests on the bed of the stream. Simons et al. (1984) report that the wash load for the Kansas River is mostly fine silt and clay and that the source of the wash load is the tributary streams and not the Kansas River itself. The bed material load is sediment that is larger than the wash load material. The bed material load is dominantly sandsized based on material sampled from the bed of the Kansas River (Figure 3.12; Simons et al., 1984). The bed material load is further subdivided into the suspended bed load that is transported throughout the water column, and the bed load that is transported close to the bottom of the river. Suspended load as used by geologists includes the wash load and the suspended bed load described here. The sediment load in the Kansas River has been sampled periodically by the U.S. Army Corps of Engineers (USACE) and by the U.S. Geological Survey. The basic method for sampling sediment load is to capture water and sediment samples at various depths along one or more vertical paths for a given cross section. The sampler rarely obtains samples from the lowest portion of the river. Thus, the sampler collects the wash and suspended bed loads. The sediment load is then determined by a depth integration method along with an adjustment factor to account for the bed load component. Simons et al. (1984) compared the sediment load values determined for the Fort Riley, Wamego, Lecompton, and De Soto USGS gaging stations with data on the rate of sediment accumulation in reservoirs on tributary streams and determined that the sediment load values were acceptable.
FIGURE 3.12--Gradation curve for sediment collected in the bed of the Kansas River near the De Soto USGS gaging station from Simons et al. (1984).
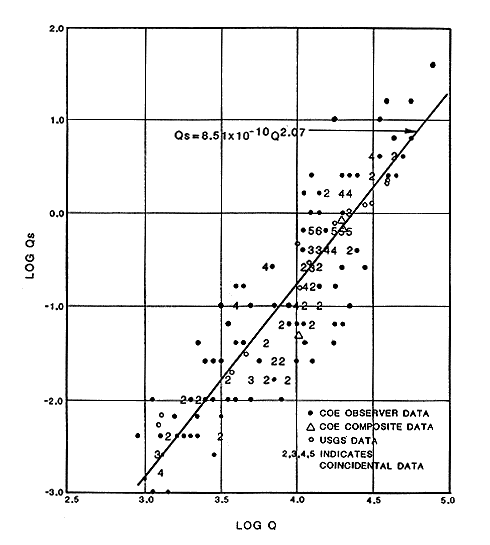
The relationships between sediment load and the hydraulic characteristics of a river are extremely complex. As was mentioned earlier, the sediment-carrying capacity of a river (sediment discharge or the volume of sediment passing through a cross section per unit time) is a function of the supply of sediment, the mean velocity and depth of the water, and the slope and cross section of the channel. The mean velocity can be calculated by dividing the discharge by the cross sectional area that is underwater. As has been highlighted in this section, many of these hydraulic characteristics are highly variable. Figure 3.13 is a log-log plot of the daily sediment discharges and daily discharges for the De Soto USGS gaging station. One can see that a one to two order-of-magnitude variation in sediment discharge exists for any given water discharge. An empirical relationship between sediment discharge and water discharge can be developed from the data in Figure 3.13. Simons et al. (1984) performed a least-squares regression analysis on the sediment discharge data and developed equations relating sediment discharge to water discharge for the Fort Riley, Wamego, Lecompton, and De Soto USGS gaging stations. Daily mean water discharges were plugged into the sediment discharge equations in order to determine the daily sediment load at each location. These daily sediment loads were then summed to get an average sediment load for a year. From the above, Simons et al. (1984) determined that at the De Soto USGS gaging station, the river is carrying about 1.67 million tons of sand per year. Lecompton, Wamego, and Fort Riley sections have carrying capacities of 1.37, 1.21, and 1.26 million tons of sediment per year, respectively. It should be reemphasized that a large variation exists in the sediment discharge versus the water discharge. Simons et al. (1984) admit that a 5% chance exists that the actual value for the yearly sediment capacity is either 3 to 4 times higher or 3 to 4 times lower than the calculated value. A 50% chance exists that the actual value is either 1.5 times higher or lower than the calculated value.
FIGURE 3.13--Graph showing the log of the measured sediment discharge (Qs in ft3/s) versus the log of the water discharge (Q in ft3/s) for the De Soto USGS gaging station from Simons et al. (1984).
Incipient Motion Analysis
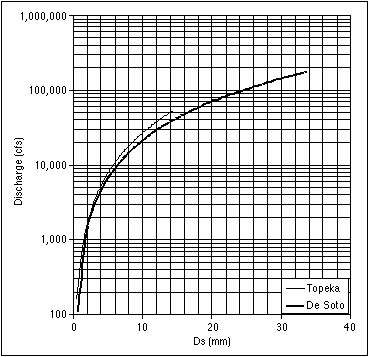
The hydraulic characteristics also control the maximum sediment size that can be transported by the river (incipient size). The incipient size is a function of the bed shear stress, the density of the sediment grains, and the Shields parameter. The bed shear stress is the stress that the water applies to the sediments and is a function of the flow velocity and other parameters. The unit weight of the sediments is approximately 165.4 lb/ft3. The Shields parameter is a value between 0.03 and 0.06. For the purposes of this analysis, a Shields parameter of 0.045 was used. Combining the incipient motion analysis with the synthetic rating curves developed earlier in this section, a plot was generated that relates the maximum transportable grain size to the discharge (Figure 3.14). Previously in this section the discharges that were exceeded 50% and 10% of the time were established for the Topeka and De Soto USGS gaging stations. By locating these discharge values on the appropriate curves in Figure 3.14, it can be seen that the incipient size for the Topeka USGS gaging station is up to 2.7 mm and for the De Soto USGS gaging station is up to 3.5 mm. These sediments are sand size (0.075 to 4.75 mm). For discharges that are exceeded only 10% of the time, the incipient sizes are up to 7 mm and 8 mm (fine gravel) for Topeka and De Soto, respectively. If dredging removes sediments larger than the river can transport, then the larger grains will be depleted from the deposits.
FIGURE 3.14--Graph showing the relationship between the maximum transportable grain size (Ds) and discharge at the De Soto and Topeka gaging stations.
Hernán A. M. Quinodoz, Kansas Geological Survey
This section examines the morphological changes observed in the Kansas River since data were first kept and identifies their most likely causes. This is a selective review of the study conducted by Simons et al. (1984) for the U.S. Army Corps of Engineers (USACE hereinafter), which is the most recent comprehensive study of the Kansas River. Other studies have focused on particular aspects of fluvial hydraulics, such as historical channel migration (Dort, 1979), streambank erosion (USACE, 1978; USACE, 1982; Osterkamp et al., 1981), and streambed degradation (Furness et al., 1967).
FIGURE 3.15--Processes affecting sediment transport in a river channel
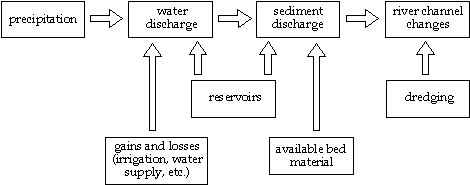
From the point of view of hydraulics, a river channel is a system that carries both water and sediment. This system is dynamic and over time it adjusts to changes in inputs and other conditions. These changes can be due to natural processes (e.g., precipitation), or the result of human activities (e.g., narrowing of the floodplain with levees), as illustrated schematically in Figure 3.15. The response of the river may take different forms, including changes in velocity and channel cross section, increased or decreased sediment-transport capacity, erosion or deposition in selected reaches, increase or decrease in bank stability and even major morphological changes (e.g., island formation, meander migration).
Simons et al. (1984) analyzed data from varied sources to identify possible trends in selected variables: median sediment size in bed load and suspended load, water and sediment yield, bank erosion, aggradation or degradation of the main channel, and island or bar formation. Because these characteristics of the river vary with time and location, they can sometimes be correlated to causal factors; this is not possible when the data lack identifiable trends. The following subsections analyze the changes in those characteristics that have been positively linked to major causal factors.
Impact of Major Floods
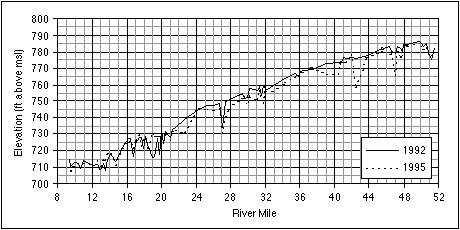
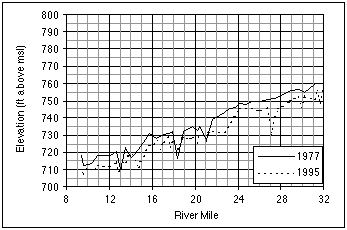
The 1951 flood had dramatic and long-lasting effects on the Kansas River. The flood itself was the largest on record, both in terms of the peak flow and overall duration. During floods the river can move sediments of larger sizes and transport larger volumes of sediments; floods of long duration cause bed degradation, bank erosion, and sometimes meander cutoff. All these effects took place at different locations in the river during the 1951 flood. The result was a general erosion of the streambed, enlarged cross sections, and a straightened main channel. An example is the approximately 2 feet (0.6 m) of bed degradation at Wamego (Simons et al. 1984), where the channel has been stable since the 1951 flood. A more recent example is the widespread bed degradation in the lower Kansas River between 1992-95, illustrated in Figure 3.16. The thalweg profile was lowered almost everywhere (5 feet [1.5 m] is a typical value), with the exception of some cross sections between river miles 12 and 20, which registered some aggradation. Although the effects of dredging and flooding cannot be separated, a fraction of the total degradation can be attributed to the 1993 flood.
FIGURE 3.16--Thalweg profiles of the lower Kansas River, before and after the 1993 flood.
Simons et al. (1984) conducted detailed year by year calculations of sediment transport, and determined that at the time of their analysis the river was still recovering from the changes associated with the 1951 flood. For example, the increased island and bar formation observed since 1951 is part of the adjustment process that tends to find a new equilibrium between the river morphology and the current hydrologic regime. After the 1951 flood, channel cross sections were relatively larger than before the flood. When discharges return to normal levels, both flow velocity and sediment-carrying capacity are relatively smaller than before the flood, resulting in aggradation of the streambed. This is a gradual process that continues until a new equilibrium is reached. However, its typical time scale can be between one and two orders of magnitude larger than that of the disturbance: where a flood event may last a few months (see peaks in Figure 3.4), the recovery may last 30 years.
Impact of Dams Built in the Last Few Decades
Eighteen reservoirs have been built in the Kansas River watershed since 1949, and are primarily operated for flood control. The regulation of flows by the dams decrease the frequency of both very high and very low flows, while increasing the frequency of occurrence of most other discharges. The analyses of Osterkamp et al. (1981) and Simons et al. (1984) demonstrate that intermediate flows have increased in frequency since the closing of each reservoir in the tributaries of the Kansas River. In these analyses intermediate flows were defined as those with a probability of exceedance between 3% and 25%; these figures are specific to the Kansas River, since they depend on both the hydrologic regime and the operating policies of the existing reservoirs.
Peak flows are catastrophic events that can carry disproportionate amounts of sediment and alter the river morphology as discussed earlier. The incipient motion calculations of Simons et al. (1984) indicate that the maximum size of sediment that can be transported by high flows has decreased by about 50% since the dams were built. Thus, the new regime of regulated discharges has a parallel impact on the sediment-carrying capacity of the river, which has less variability than without the dams.
Another major effect of the reservoirs is the trapping of sediment. The release of clear water with an unsatisfied sediment-carrying capacity has resulted in pronounced streambed erosion immediately downstream of each reservoir. However, this effect tapers off within a few miles of the dam, so that the erosion is mostly confined to the tributaries; Simons et al. (1984) reported measurable but moderate streambed erosion (1-2 feet [0.4-0.6 m]) in the Kansas River at the confluence with each tributary having an existing reservoir. They also indicated that the compound effect of all reservoirs is a decrease in the total sediment yield (volume of sediment transported), and a coarsening of suspended sediment. For example, at the Wamego gaging station, the median suspended-sediment size (d50) has increased from 0.002 mm (claysize) to 0.007 mm (siltsize) between 1957 and 1977 (Osterkamp et al., 1981).
Impact of Dredging in the Lower Kansas River
Analyzing the impact of dredging can be greatly aided by knowing what type of sediment is available in the channel bed. Such an analysis was conducted for the Kansas River by Simons et al. (1984). Their results are shown in Figure 3.17, which depicts the median particle size (d50) of the bed material as a function of river mile. The d50 is remarkably homogeneous along the river. For the upper and middle reaches, d50 ranges from 0.4 mm to 2 mm, almost a perfect overlap with the medium sand range of the Unified Soil Classification. Most of the lower Kansas also has the same range of particle sizes. Historic plots show that the range of d50 values has not changed significantly between 1956 and 1983 (Figure 3.18). The middle portion of the Kansas River for this part of the study is the reach from Bowersock Dam to just west of Topeka that includes the area of present and previous dredging (approximately R. M. 52-95).
FIGURE 3.17--Variability of bed material in the Kansas River. Median particle size (d50) in mm as a function of river mile, corresponding to 1983 conditions (after Simons et al., 1984). A larger version of this figure is available.
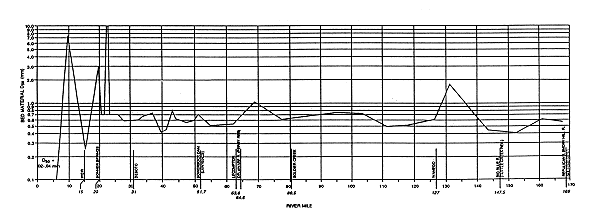
FIGURE 3.18--Variability of bed material in the Kansas River. Median particle size (d50) in mm as a function of river mile. The four historic profiles correspond to the years 1956, 1962, 1976, 1983 (after Simons et al., 1984). A larger version of this figure is available.
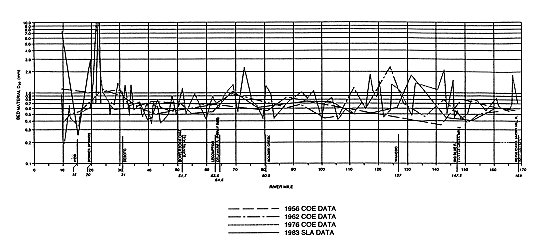
These figures suggest a simple picture of the Kansas River. The middle and upper Kansas can be considered one unit that shares common characteristics, primarily in terms of sediment-size distribution and sediment yield. Also, the middle and upper Kansas have not been heavily exploited by dredging, except near Topeka. The Kansas River upstream of Bowersock Dam has a relatively stable morphology (Simons et al., 1984), with the exception of an area around Topeka, where 1-2 feet (0.3-0.6 m) of bed degradation have been observed; however, this is in an area where the channel has been narrowed with flood-control works, making it difficult to separate those effects from the effects of dredging.
The lower Kansas River is different from the upper and middle Kansas in several ways, including the backwater effects from the Missouri River (examined in the next subsection) and the presence of gravel deposits. In addition, the lower Kansas has been heavily dredged in the last few decades, with significant bed degradation in extensive areas. In the reach between the Turner bridge (R. M. 9.6) and Bonner Springs (R. M. 20), channel bed elevations have dropped by 8 to 10 ft (2.4-3 m). Dredging activities can have significant local effects, since typically dredges can leave a hole 20 to 30 ft (6.1-9.1 m) deep; if the dredge is allowed to sweep a whole cross section, effects can be felt on the banks as well. Sustained dredging activity on a given reach can cause significant bed degradation over time, as illustrated in Figure 3.19. Present restrictions on dredging permits administered by the USACE (Appendix A) require that a minimum of 100 feet (30 m) from all river banks be left undisturbed; larger distances are required along major bends in the river.
FIGURE 3.19--Thalweg profiles of a 24-mile (38.4 km) reach in the lower Kansas River. The decrease in bed elevation is the result of almost 20 years of dredging in the area (source: USACE surveys).
Dredging activities are constrained by the availability of sediments of the desired size and by the capacity of the river to transport them. Sediments are transported either in suspension (suspended load) or pushed along the stream-bed (bed load). However, the origin of the different sediment sizes transported by the Kansas River is more relevant to our discussion. The fine materials (silt and clay sizes) originate in the tributaries (wash load), while coarser materials (sand and gravel sizes) originate in the stream-bed of the Kansas River (bed material load). As discussed earlier in this subsection and depicted in Figure 3.12, bed-material load is composed almost exclusively of sand. Furthermore, the incipient motion calculations detailed in the previous section demonstrate that gravel-size material cannot be transported by the river under the present hydrologic conditions, except during large floods. Hence, as observed by Simons et al. (1984), the gravel currently being mined at select locations is part of ancient deposits and will not be replenished when exhausted.
Impact of Miscellaneous Factors at the Local Scale
Other factors also play a role in the hydraulics of the Kansas River, but their impact is restricted to local areas (as opposed to whole reaches of the river). Although not of primary interest to this report, these factors have been mentioned in previous reports and deserve mention to keep their impact in perspective.
Hernán A. M. Quinodoz, Kansas Geological Survey
The likely effects of future dredging are analyzed in this section. Ways of assessing and managing its environmental impacts also are examined. This analysis aims to provide factual information to decision-makers considering alternative uses of the river. But because this analysis is focused only on the river hydraulics, it is just one piece of a larger puzzle. Social and economic objectives also have to be considered and properly weighted in making these types of decisions; often times they end up being the decisive factors. Some economic impacts are discussed in Chapter 2.
Predicted Effects of Dredging in Areas Without Significant Past Dredging
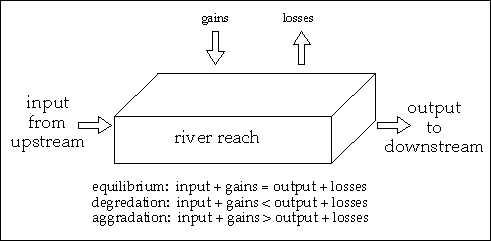
Understanding and quantifying sediment transport processes only requires a simple sediment budget equation:
d VOL(t)/ dt = SDin(t) - SDout(t) + GAIN(t) - LOSS(t).
This budget equation is applicable to an arbitrary reach of the river defined by two transverse cross sections, as shown schematically in Figure 3.20. The four terms in the right-hand side of the equation are the sediment additions and subtractions: SDin(t) and SDout(t) are the sediment discharge passing through the upstream and downstream boundaries of the reach, respectively; GAIN(t) and LOSS(t) are the additions and subtractions, respectively, that occur anywhere inside the river reach considered. The term GAIN(t) includes sediment input from tributaries and sediment brought to the stream by overland runoff; LOSS(t) accounts for sediment extraction by dredging and flood deposits in the floodplain. All terms in the above equation are functions of the time t, as indicated by the variable t in parenthesis. The result of the four terms described is the rate of change in the total volume of sediment VOL(t), indicated as {d VOL(t)/ dt}. For example, a negative value of {d VOL(t)/ dt} corresponds to a net loss of sediment in the reach.FIGURE 3.20--Components of a sediment budget on a reach of a river channel.
In practice, measurements are taken and evaluations of these terms are made only at discrete time intervals (t1, t2). Then the above equation can be rewritten as
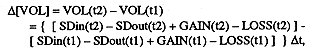
![]()
where W is the width of the average channel cross
section, L is the length of the reach studied,
![]() is the
average change in bed elevation, and p is the porosity of
the sediment. If for a given reach the width of the channel
W is not changing, then the change in sediment
volume results in aggradation or degradation of the channel,
and its average magnitude is equal to
is the
average change in bed elevation, and p is the porosity of
the sediment. If for a given reach the width of the channel
W is not changing, then the change in sediment
volume results in aggradation or degradation of the channel,
and its average magnitude is equal to ![]() .
.
Given the appropriate information to evaluate sediment additions and subtractions, the above equations are all that is needed to assess morphological changes in a river reach as a function of time. For an actual evaluation, it might be convenient to carry out separate budgets for different sediment sizes (e.g., coarse sand, medium sand, fine sand). This procedure only adds to the number of calculations, but the concepts remain the same.
Applying the above approach to the Kansas River is straightforward, since most reaches are either in equilibrium or slightly degrading (Simons et al., 1984). In a reach where incoming and outgoing sediment discharges are approximately equal, an additional extraction via dredging means a decrease in the sediment inventory of that reach and further degradation. In that case, the annual degradation D[BE] can readily be evaluated as a function of the yearly extraction rate (LOSS). This situation can be undesirable, if the magnitude of the streambed degradation is greater than acceptable levels at a given location.
The same sediment budget can be applied to the river as a whole, but with a significant difference. The Kansas River immediately near the confluence with the Missouri River is aggrading, depositing silt on top of the existing sand (Simons et al., 1984). The backwater effect caused by the high water levels in the Missouri River creates a reach with velocities so low that even fine sediment particles cannot be transported. Since larger sand particles also cannot be transported, the outflow of sand is nil (SDout = 0). Assuming no additional sediment sources (GAIN = 0), maintaining the present channel unchanged (D[BE] = 0) requires that the incoming sediment discharge (SDin) be removed from the reach by dredging (LOSS). In the absence of dredging, there would be aggradation (D[BE] > 0) in part of the reach considered.
A possible management strategy for the situation described above would be to allow dredging to be a fraction of the incoming sediment discharge. However, first the magnitude of the incoming discharge has to be estimated, which is not a simple task. As previously discussed, both measurements and calculations of sediment discharge vary over a wide range of values, sometimes up to two orders of magnitude for a given value of streamflow (Figure 3.13). This uncertainty carries over to other calculations based on these measurements, such as the average annual sediment yield. Average values filter out part of the initial variability, but still carry some uncertainty. Consider the mean values of annual sand load calculated by Simons et al. (1984) for three stations in the Kansas River:
| Station: | Wamego | Lecompton | De Soto |
|---|---|---|---|
| Sand load: (Mtons/yr) | 1.21 | 1.37 | 1.67 |
These figures are based on the relationships between streamflow and sediment discharge such as the one displayed in Figure 3.13. Without a detailed evaluation, it is impossible to say what fraction of that uncertainty will correspond to the mean annual values. For illustration, assume that the mean is affected only by a 50% uncertainty; then the above estimates become ranges when multiplied by 0.5 (minimum) and 1.5 (maximum). For example, the sand load at De Soto would be between 0.8 and 2.4 Mtons/yr. These figures are only illustrative, but serve to make an important point: there is significant and often irreducible uncertainty in dealing with sediment transport. Experts are usually content with estimating the right order of magnitude for most assessments. The practical implication is that in order to make decisions involving these variables, one has to develop not only a best estimate, but also a realistic range defined by minimum and maximum values. More accurate evaluations are possible utilizing probabilities and making decisions in terms of risk, but the details are beyond the scope of this study.
Assessing and Managing the Impacts of Dredging
The key to assessing change in natural systems is to gather select information by way of a carefully designed monitoring program. That information, when enriched by focused analysis, can form the basis of management decisions. The recent USACE regulations that apply to new dredging permits in the Kansas River (USACE, 1990) are a good example. These regulations, listed in Appendix A, are based on periodic monitoring of channel cross sections and a sequence of decisions linked to the results of that monitoring.
The USACE regulations establish constraints that trigger specific actions, conforming an adaptive management strategy. For example, the average streambed degradation in a cross section cannot exceed 2 feet (0.6 m). If this level is reached, dredging operations can be suspended. The USACE reviews the periodic cross section surveys, which have to be conducted by independent consultants hired by the dredging operators. Other constraints written in the regulations pertain to the maximum acceptable hole size, rates of sand and gravel extraction, and dimensions of a buffer zone between adjacent dredging operations. Such adaptive management is very appropriate to deal with fluvial systems that are constantly adjusting to change. It allows a case by case management at the local scale (individual dredging permits) based on sitespecific information.
Need for Further Study
The discussion in the previous two subsections provides some preliminary answers to questions that deal with the overall behavior of the fluvial system. A logical next step might involve making detailed analyses and calculations for selected reaches. However, this requires considerably more resources, including the acquisition of additional data to assess the system response on a continuous basis. Possible objectives of the assessment include: identifying stream reaches with different hydraulic characteristics (e.g., high velocities, erodible banks); evaluating the sediment budget and trends, given the current transport and extraction rates; and assessing how long sand will last at current extraction rates. An initial assessment for the whole river would provide a baseline condition against which further change can be compared. The study of Simons et al. (1984) might be considered such a baseline, although the level of detail might not be satisfactory for the middle and upper Kansas River. Ideally it would be necessary to repeat the overall assessment every five or ten years to evaluate the changes in morphology that occur in response to both natural and humaninduced stresses.
Detailed analyses usually take the form of a mathematical model that quantifies sediment-transport processes in terms of parallel equations for the conservation of water and sediment. However, all models, simple and complex, need appropriate and reliable data. In dealing with fluvial dynamics, such data include not only the forcing functions (precipitation, overland runoff, discharge from tributaries, discharge from reservoirs) but also select measures of the system response (changes in channel cross sections, stagedischarge relationships, and sediment-load measurements).
Acquiring such information would involve considerable effort. Describing the geometry of the river channel requires surveying closely spaced channel cross sections (e.g., 1 mile [1.6 km] apart), and water levels measured at each cross section periodically (a few times per year). For sediment transport the key parameter is the mean velocity; its calculation requires both the volumetric (water) discharge, estimated at the nearest gaging station, and the cross sectional area. The area of the cross section needs to be measured frequently if bottom degradation and bank erosion are suspected or need to be determined. Periodic sampling of sediment load (both bed load and suspended load) is of critical importance; this should be done at properly chosen locations (typically at each measured cross section). Thus, hydrographic surveys and sediment load sampling are integral parts of any sediment-transport study.
Developing a full-blown mechanistic dynamic model with detailed crosssections, tracking the evolution of many key variables as function of time, is not always necessary. Although such a model would provide a vast amount of information and insight, it might not be necessary to address some of the questions that managers and rivers users might want to address. In some cases an empirical model based only on statistics might be enough to assess trends and empirical relationships between the main variables. The key here is that regardless of the model entertained, detailed periodic information is necessary. Only an appropriately designed monitoring program can deliver that type of information.
However, providing quantitative answers to questions involving sediment transport is not an easy task, even when significant amounts of information are available. This is so because our knowledge of sediment-transport relationships is far from being an exact science. Measurements exhibit significant scatter, and in practice, one is usually content with making order-of-magnitude calculations and statements. Making sound decisions based on this type of information requires a probabilistic approach that weighs the risks associated with each possible outcome.
Blechinger, E. T., 1997, An analysis of sand mining alternatives along the Kansas River basin: Kansas Geological Survey, Open-file Report 97-66, 86 p.
Dort, W., Jr., 1979, Channel migration investigation, historic channel change maps, Kansas River and tributaries, bank stabilization component, Kansas and Osage rivers, Kansas study (conducted for the U.S. Army Corps of Engineers, Kansas City District): University of Kansas, Department of Geology.
Furness, L. W., Albert, C. D., and Leonard, R. B, 1967, Kansas River, Bonner Springs to mouth--Degradation of channel: U.S. Geological Survey, Open-file Report 67-93, 18 p.
Osterkamp, W. R., Curtis, R. E, Jr., and Crowther, H. G, 1981, Sediment and channelgeometry investigations for the Kansas River bank stabilization study, Kansas, Nebraska, and Colorado: U.S. Geological Survey, Water-resources Investigations, Open-file Report 81-0128, 71 p.
Simons, Li, and Associates, 1984, Analysis of channel degradation and bank erosion in the lower Kansas River: MRD Sediment Series Report No. 35, for the US Army Corps of Engineers, Kansas City District, Kansas City, Missouri.
U.S. Army Corps of Engineers, 1978, Kansas River bank stabilization study, plan of study: U.S. Army Corps of Engineers, Kansas City District, Kansas City, Missouri
________, 1982, Stage 2 ReportWater supply, mineral intrusion, and bank stabilization in the Kansas and Osage rivers, Kansas: U.S. Army Corps of Engineers, Kansas City District, Kansas City, Missouri.
________, 1990, Commercial dredging activities on the Kansas River, Appendix A--Regulatory Plan: U.S. Army Corps of Engineers, Kansas City District, Kansas City, Missouri.
Previous Page--Economic Resources
Next Page--Recreation