
Kansas Geological Survey, Ground Water Series 7, originally published in 1982
Next Page--Appendices

Originally published in 1982 as Kansas Geological Survey Ground Water Series 7. This is, in general, the original text as published. The information has not been updated.
If one wishes to know something about a large population of anything, or about the behavior of a large system, especially for predictive purposes, a sampling procedure must be designed. This is true whether the subject of interest is toothpaste preference, voter attitudes, or dwindling reserves of groundwater in the High Plains aquifer in Kansas. Regardless of the size or distribution of a sample, some statistical error will remain; a compromise must be made that balances the smallest acceptable statistical error against the economic cost of obtaining the sample.
The Kansas Geological Survey has been involved for a number of years in research dealing with sampling design for geological problems, part of a larger effort referred to as "spatial analysis." This research experience has been applied by Ricardo A. Olea to a very practical problem, the costly program of monitoring the network of observations wells that measure the water level in the High Plains aquifer (including the Ogallala). This monitoring program has developed over a period of many years without systematic planning and with a considerable investment of State and Federal resources. Because the Kansas Geological Survey contributes funding for this program, the uncontrolled expansion of the sampling network has caused us to address the question of the number and configuration of observation wells required to characterize the water table of the High Plains aquifer with an acceptable error, at an acceptable cost. The U.S. Geological Survey, a cooperator in the groundwater program in Kansas and in other states, has recently defined network analysis as a high-priority concern, again because of uncontrolled costs. This report should provide a model for U.S.G.S. efforts.
The results of our sampling-design study of the High Plains aquifer are clear. A redesigned network will allow a reduction in the number of observation wells that must be monitored without significantly increasing the errors in the estimates of the water table elevation. The monetary savings can provide funds to expand the network into areas that are now inadequately sampled, or a reduced network can be operated at lower cost without significantly degrading the quality of the information. Some local government users of information from the existing network are reluctant to accept the findings of this report. While a sampling network more dense than the one suggested here would not be incompatible with Olea's recommendations, the cost may not be justifiable. Hard decisions must be faced as to who will pay for the additional information.
![]()
State Geologist and Director, Kansas Geological Survey
The network of observation wells which monitor the water table of the High Plains aquifer in Kansas has developed without systematic planning over a period of many years. The efficiency of this network can be evaluated by sampling design procedures based on universal kriging, an estimation method that is part of the statistical theory of regionalized variables. Information gathered by the High Plains observation well network is used primarily as input to hydrologic models and to assist in decision-making by groundwater managers responsible for controlling the exploitation of the aquifer. It was found that the present observation well network is not optimal because of the haphazard location of observation wells. An alternative network designed in a hexagonal stratified pattern would allow a reduction in the number of observation wells from 1749 to 1135 without significantly changing either the average standard error of the water table elevation [currently at 12 feet (3.7 m)] or the form of the contour map of water table elevations. Monetary savings achieved by reducing the number of wells could be used to operate the network at a lower cost or could provide funds to measure wells in inadequately sampled areas; this would allow reduction of the maximum standard error from its present value of 36.6 feet (11.2 m)to 13.3 feet (4.1 m).
Groundwater is a vital resource in areas with insufficient alternative surface sources of water or with unfavorable annual precipitation. In western Kansas, the High Plains aquifer provides about 95 percent of all the water for irrigation. Prior to 1930, agriculture consisted primarily of dryland farming and cattle grazing. Although groundwater irrigation technology was developing on the Plains, the number of irrigation wells did not increase substantially until after the drought of the 1930's. The agricultural economy of the State developed rapidly because of the availability of low-cost energy and water. However, the situation has reversed in recent years because the cost of pumping is increasing and the water level in the wells is declining. In some areas the economics of the situation have deteriorated to the point where irrigation is no longer profitable and farmers are returning to dryland farming (Gutentag and Weeks, 1980). At the present pumping rate, most of the State will be forced to return to dryland farming by the turn of the century.
Although pumping costs are out of control, groundwater depletion can be avoided with judicious management. If an aquifer is not disturbed by man, it is inexhaustible at the human scale of time because over the long run the recharge equals the discharge. This equilibrium often is disturbed by seasonal and climatic changes. Ideally, a well-managed aquifer can tolerate some artificial upstream pumping provided the material balance is not altered by total natural and artificial withdrawals larger than the recharge. An aquifer, in terms of the use of the resource, can be considered renewable or non-renewable depending on the pumping rate. Under excessive pumping, the aquifer will behave like an oil field which eventually becomes depleted. A properly managed aquifer, on the other hand, is an eternal source of water.
State and federal agencies having regulatory responsibilities over natural resources began monitoring the water level through scattered observation wells which became more numerous as the decline in water level became a real concern. The number and location of observation wells did not follow any rational guidelines; rather, the number of monitored wells increased as if more accurate observation of the effects of depletion would cure its causes. At the present time, the depth to water is measured every winter in more than two thousand observation wells around the State. The budget for measurements in the 1981 season was $106,000 (U. S. Geological Survey, 1980). Over the years, the adequacy of the network has been the subject of several conversations and meetings, but with no final resolution. Contradictory opinions have been expressed, as some believe even more observation wells are necessary and others consider that the network is already too expensive to operate and there should be no increase in the number of wells. The lack of a consensus has been partly due to the absence of basic information in network design on which to establish a scientifically sound decision. The existing literature presents a few partial studies of observation networks, primarily in the area of mining. The findings are not conclusive and are difficult to extrapolate to geohydrology.
The Kansas Geological Survey has both an academic and economic interest in the problem. The Geohydrology Section is by far the main research user of observation well data. The operational costs of the network are shared approximately equally between the federal government, represented by the U. S. Geological Survey, and the State of Kansas, represented by the Division of Water Resources and the Kansas Geological Survey.
The analysis of the Kansas groundwater observation well network is not an isolated problem, but rather an example of the more general problem of data collection for the purpose of characterizing phenomena such as the porosity in a rock formation or the Earth's gravitational field, which are functions of geographical coordinates, or spatial functions. The Kansas Geological Survey decided to sponsor a project to evaluate the Kansas groundwater observation well network and also to investigate the more general problem of the sampling of spatial functions. The project has produced a methodology which requires only the use of a hand calculator and tables (Olea, 1982a, 1982b). Using these simple tools, it requires only a few minutes to design an optimal sampling procedure which will achieve a specified level of accuracy when applied to a spatial function. The methodology is the backbone of this exhaustive study of the High Plains aquifer observation well network in the State of Kansas. The main objectives of the study are:
This chapter is a brief presentation of the methodology used to design an optimal observation well network for the High Plains aquifer in Kansas. A more complete discussion will be found in Olea (1982a, 1982b).
A water table is a special case of a more general type of n-dimensional surfaces called spatial functions. Mathematically, a spatial function is an association of numbers to a domain of geographical coordinates. Some spatial functions, such as the water table elevation, are time dependent; others, such as the thickness of a geological formation, are invariant at the human scale of time.
Typical spatial functions are continuous and uniquely defined over sizable domains. Some, such as geothermal gradients, are not easily measurable and present an expensive and time-consuming problem in terms of the effort required for their accurate characterization. Commonly, such functions are known only partially through a scattered set of observations. In statistical jargon, the selected observations are called a sample (James and James, 1976, p. 339) and each individual measurement is called a sample element (Williams, 1978, p. 27).
Even if the observations have been carefully taken to avoid measurement error, the spatial function is only known with certainty at the sampled locations. The exact value of the spatial function at unsampled locations is subject to uncertainty, as no method has yet been devised which will yield error-free estimates. Even though there might be only one value of the spatial function at any location in the sampling domain, the unknown estimated value is more thoroughly described by a collection of likely values than by a single number. A tabulation of events and their associated probability of occurrence corresponds to the statistical concept of a probability density function (Hogg and Craig, 1979, Section 1.6). In statistical terms, a quantity which may take any of the values of a certain set with a specified relative frequency is called a random variable or a variate (Rendall and Buckland, 1971, p. 162). There will be as many random variables as locations in the sampling domain. The set of all random variables associated with a given spatial function constitutes what is known as a random function (Matheron, 1971, p. 50).
Listing a random function describing a spatial function is a cumbersome task. It would be desirable to summarize the function in an informative, short description rather than listing all its possible outcomes. For this purpose we may invoke the use of mathematical expectations. The average of all possible outcomes of a variate weighted by their probability of occurrence is the mean and represents a central value of the population. The weighted average of the squares of the differences between the outcomes and the mean is the variance (Hogg and Craig, 1970, p. 46). The square root of the variance is the standard deviation. As the variance becomes larger when the differences increase, the variance and the standard deviation are a measure of the dispersion of the outcomes relative to the mean value. The standard deviation could also be interpreted as a measure of the uncertainty as to the true value of the spatial function. A small standard deviation indicates the outcomes are clustered tightly around the central value over a relatively narrow range of possibilities. Conversely, a large standard deviation indicates that the actual value could be any of a larger range of possibilities.
The theory of regionalized variables is a set of statistical principles which describe spatial functions and their sampling without regard to the physical nature of the variable under study. Universal kriging is an estimation method based on regionalized variable theory presenting the unique peculiarity of providing both unbiased estimates of spatial functions and a measure of reliability associated with each of those estimates. For these reasons, universal kriging is particularly suited to estimating the central value and the dispersion of the variates used in spatial function modeling.
Spatial functions which satisfy certain basic assumptions in the theory are called regionalized variables. The term geostatistics has come to mean the specialized body of statistical techniques originally developed in France by Prof.G. Matheron and his associates to treat regionalized variables (Matheron, 1965, 1971). Typical spatial functions amenable to estimation using geostatistics include the ore content in a mineralized body; the porosity of sedimentary rocks; the amount of precipitation per square mile; and the elevation of the tops of subsurface formations. Fluctuations in space- and time-dependent data are erratic and often unpredictable from one location to another, but by and large there is an underlying trend in the fluctuations which precludes regarding the data as the result of a completely random process. Closely spaced samples, for example, typically are statistically autocorrelated. In certain instances sample elements, such as the drill cores used to essay ore grades, have size, shape, and orientation. The spatial characteristics of a sample element constitute what is called the support.
The intrinsic hypothesis is a stationarity constraint used for purposes of statistical inference. Let Z(![]() )and Z(
)and Z(![]() ) be two of the random variables comprising the regionalized variable. The arrow (→) over the geographical coordinate indicates a vectorial property, implying orientation and magnitude in n-dimensional space. The difference between two random variables [Z(
) be two of the random variables comprising the regionalized variable. The arrow (→) over the geographical coordinate indicates a vectorial property, implying orientation and magnitude in n-dimensional space. The difference between two random variables [Z(![]() )- Z(
)- Z(![]() +
+![]() )] is yet another random variable. A regionalized variable is said to satisfy the intrinsic hypothesis if the difference [Z(
)] is yet another random variable. A regionalized variable is said to satisfy the intrinsic hypothesis if the difference [Z(![]() ) - Z(
) - Z(![]() +
+![]() )] is second-order stationary. In other words, a regionalized variable satisfies the intrinsic hypothesis if, for any displacement h, the first two moments of the difference [Z(
)] is second-order stationary. In other words, a regionalized variable satisfies the intrinsic hypothesis if, for any displacement h, the first two moments of the difference [Z(![]() )- Z(
)- Z(![]() +
+![]() )]are independent of the location
)]are independent of the location ![]() and are a function only of
and are a function only of ![]() :
:
E [Z(![]() ) - Z(
) - Z(![]() +
+![]() )] = M(
)] = M(![]() ) (2.1)
) (2.1)
E [{Z(![]() ) - Z(
) - Z(![]() +
+![]() ) - M(
) - M(![]() )}2]= 2γ(
)}2]= 2γ(![]() ) (2.2)
) (2.2)
In the specialized language used in geostatistics, M(![]() ) and γ(
) and γ(![]() ) are referred to as the drift and the semivariance or intrinsic function. The units of M(
) are referred to as the drift and the semivariance or intrinsic function. The units of M(![]() ) are the same as the units of Z(
) are the same as the units of Z(![]() ), and the units of γ(
), and the units of γ(![]() ) are the square of the units of Z(
) are the square of the units of Z(![]() ). Provided the intrinsic hypothesis is met, both moments can be estimated.
). Provided the intrinsic hypothesis is met, both moments can be estimated.
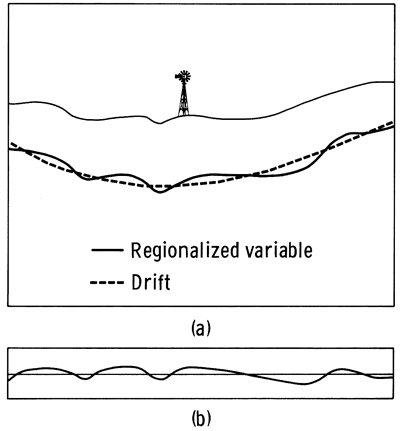
There are a few important circumstances under which geostatistics can be applied even if the intrinsic hypothesis does not hold. Of special interest is the situation when the regionalized variable is not first-order stationary because the drift has a systematic trend, as shown in Figure 2.1. Removing the drift from the regionalized variable results in a difference called the residual. Regionalized variable theory is still applicable if the intrinsic hypothesis holds for the residuals.
Figure 2.1--Basic elements in the theory of regionalized variables. (a)Regionalized variable and drift. (b)Residual after subtraction of the drift from the regionalized variable.
Structural analysis is the term applied to the study of semivariograms for the purpose of extracting information about the nature of fluctuations in a regionalized variable. Appendix A contains a detailed structural analysis of the water table elevation in the High Plains aquifer in Kansas.
Universal kriging is a linear estimator within the regionalized variable theory and has the form:
Z*(![]() 0) = ∑kj=1λjZ(
0) = ∑kj=1λjZ(![]() j)(2.3)
j)(2.3)
Finding the set of weights λj's which minimizes the estimation variance under the constraint that the estimator must be unbiased is a linear programming problem. The final product of universal kriging estimation at a given location ![]() 0 consists of two numbers: the estimated value of the spatial function and the estimation variance.
0 consists of two numbers: the estimated value of the spatial function and the estimation variance.
The standard deviation of an unbiased estimator is called the standard error (James and James, 1976, p. 139). Since the standard error is given in the same units as the regionalized variable itself, it is more commonly used as a measure of uncertainty in the estimate than is the estimation variance. Universal kriging is the only spatial function estimation method that provides a standard error of the estimate.
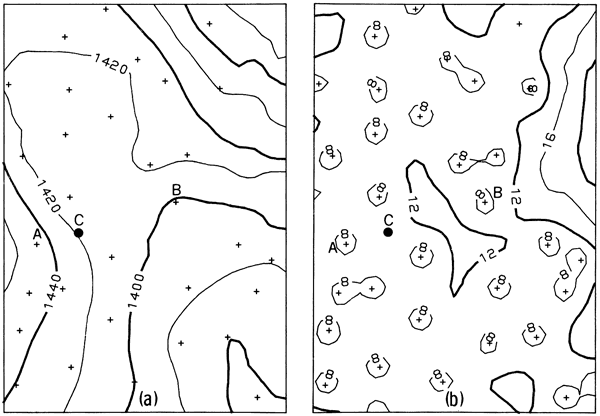
If universal kriging is repeatedly performed for discrete locations within the area of interest, the estimates can be passed to a graphical display package to create spatial representations of the regionalized variable. Possible forms of representation include block diagrams, cross-sections, or contour maps of either the variable itself or the standard error of the variable. Figure 2.2a is a graphical solution of the problem of continuously representing a spatial function known only at discrete points and Figure 2.2b shows the corresponding standard error map.
Figure 2.2--Graphic representation of the results of universal kriging of a two-dimensional spatial function. Crosses represent locations of sample elements. (a) Most likely representation of the spatial function. (b)Standard error.
The global performance of samples over the sampling domain of a spatial function can be judged by two indices, average standard error and the maximum standard error, which in turn depend on:
The factors which influence the sampling efficiency indices are not alike; two have nothing to do with sampling and a third is only partially related to sampling. The semivariance and drift are inherent characteristics of the spatial function. The designer of the sampling program can only select models of these characteristics that provide the best fits to the true semivariance and the drift. Specification of the size of the sample subset to be used in the universal kriging estimation equations is primarily a problem in computational efficiency, with some sampling implications. This leaves sample pattern and sample density as the only two factors which offer wide flexibility in the design of the sampling scheme.
The selection of the best sampling efficiency factors is an operations research problem which can be organized as a systematic procedure to yield an optimal solution if the problem is feasible. The procedure is subject to the following constraints: (a) The residuals satisfy the intrinsic hypothesis. (b) The physical size of the support of the sample elements and the estimated value are the same. (c) The sampling space is two dimensional. (d) The semivariogram of the residuals is linear.
all constraints are met by the data on water table elevations in the high plains aquifer. the constraints are sufficiently weak that the method should be applicable to many other spatial variables as well. the second constraint is the strongest and excludes certain special functions which are of interest in ore reserve estimation. the third constraint is satisfied in all mapping problems. even in studies of three-dimensional spaces, samples may be collected in a series of two-dimensional planes, which helps to satisfy the second constraint. the semivariance is a monotonically increasing function close to the origin. because even complex functions can be approximated by linear piecewise interpolation procedures, the problem of satisfying the fourth constraint becomes one of determining how large a portion of the semivariogram can be approximated by a straight line.
Algorithm 2.1
The following is a procedure for finding the optimal sampling method for a specified sampling efficiency index.
1. Perform a structural analysis.
2. Decide whether the average standard error or the maximum standard error is the index to be minimized.
3. Enter table 8.1 for the specified index and appropriate drift. Choose the pattern with the lowest index in the table. In case of a tie, use the pattern with the minimum alternative index.
4. Specify a value for the sampling efficiency index.
5. Compute the desired density ρ by
ρ = ω2[ I(1,1)/ I(ω,ρ)]4 (2.4)
where ω is the slope of the linear semivariogram; I(1,1) is the efficiency index in Table 8.1 for the given pattern at a density of one point per square mile (0.39 points/km2)and a semivariogram slope of one; and I(ω,ρ)is the desired level for the efficiency index of step 2.
6. Calculate the number of sample elements within the neighborhood for which the models in the structural analysis are valid.
7. Compare the number of sample elements inside the neighborhood with the minimum number of points necessary to achieve a solution of the universal kriging system of equations in table 8.3. Should the number of points inside the neighborhood be insufficient, the solution is unfeasible. In case a solution is required, go back to step 1 and redefine parameters. Otherwise, stop. If there are enough sample elements inside the neighborhood, proceed to the next step.
8. Enter table 8.2 and determine the point of no return.
9. Compare the sample elements inside the neighborhood to the point of no return. If the point of no return is smaller than the number of points that can be placed inside the neighborhood, use a number of nearest neighbors equal to the point of no return and stop. Otherwise use a number of nearest neighbors equal to the number of points inside the neighborhood.
10. Find in Appendix 8, tables 8.4 to 8.9, the selected index and appropriate drift. Take the pattern that minimizes the index for the number of nearest neighbors computed in the previous step.
11. Enter the minimum index selected on the preceding step into Equation 2.4 to recompute the optimal density.
Stop.
Appendix C contains an example of the use of the algorithm.
The theoretical review in Chapter 2 is complemented with a description of the High Plains aquifer and the present network used to monitor the groundwater level in the State of Kansas.
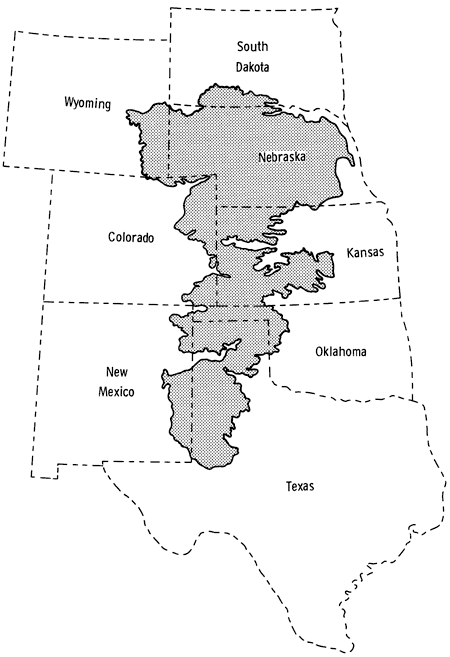
Groundwater is one of the most precious natural resources in Kansas, and among all aquifers in the State by far the largest and most important is the High Plains aquifer. An aquifer is defined as a water-saturated permeable geologic unit able to transmit significant amounts of fluids under normal pressure gradients (Freeze and Cherry, 1979, p. 47). The High Plains aquifer extends over an area of 177,000 square miles (440,000 km2), 29,000 (75,000 km2) of them in Kansas and the remainder in parts of the states of Wyoming, South Dakota, Nebraska, Colorado, New Mexico, Oklahoma, and Texas, as shown in Figure 3.1. Flat to gently rolling terrain characterizes the High Plains region, which is a remnant of a vast plain which was formed of sediments deposited by streams flowing eastward from the Rocky Mountains. Subsequently, erosion isolated the plains from the mountains. The aquifer consists, as defined by the U. S. Geological Survey (Gutentag and Weeks, 1980), of one or more hydraulically connected geologic units of late Tertiary or Quaternary age. In ascending order, the late Tertiary rocks consist of the Brule Formation, Arikaree Group, and the Ogallala Formation, the latter being the only one present in Kansas (O'Connor and McClain, 1981, p. 5). The Quaternary deposits consist of alluvial, dune-sand, and valley-fill deposits.
The High Plains aquifer is primarily a closed system, but various vertical and lateral connections with other aquifers preclude regarding it as a perfect hydrologically isolated unit. Thus, the exact boundary of the aquifer is defined differently by various authors. The boundary shown in Figure 3.1 is essentially the eroded edge of the geologic units comprising the aquifer.
Figure 3.1--Areal extension of the High Plains aquifer (after Gutentag and Weeks, 1980).
In the High Plains aquifer today, an estimated 168,000 irrigation wells are producing 30 million acre-feet (3.7 x 109 m3)of water each year which is used to irrigate about 16 million acres (64.7 x 106 km2) (Gutentag and Weeks, 1980). To judge the impact on the aquifer of pumping by more than 25,000 wells in Kansas, periodic measurements of the water table depth are made. A water table is defined as the static locus of those locations where the fluid pressure confined in a porous aquifer is equal to the atmospheric pressure (Freeze and Cherry, 1979, p. 39). The water table at a particular location is revealed by the level to which water stands in the borehole of a well deep enough to penetrate into the aquifer. For most wells, measurement of depth to water is made directly with a metallic tape lowered through a hole in the surface flange. The measurement represents depth to water in the annular space between the protective casing and the production pipe. Provided that the beginning of the scale in the tape is always at the bottom of the well, the depth to water is computed directly as the difference between the reading on the surface minus the length of the wet portion of the tape. The trickiest part of the measuring consists in guaranteeing that the tape stays straight inside the annular space.
A small fraction of the observation wells are only used to measure depth to water, but most of the wells used in the survey are producing wells. To avoid drawdown cone effects due to recent pumping in the well itself or in the surrounding wells, the measurements are taken during the wintertime when irrigation stops for several months.
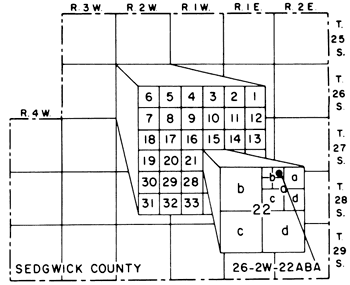
The U. S. Geological Survey, Division of Water Resources, and the Kansas Geological Survey support a program to measure, file, and report the depth to water in more than 2,000 wells throughout the State. The reported values are location, depth to water, and land surface elevation. The difference of the last two provides the altitude of the water table, called water table elevation. Location is reported in the Bureau of Land Management's system of land subdivision. In that system, the first set of digits of a well number indicates the township; the second set, the range east or west of the Sixth Principal Meridian; and the third, the section in which the well is located. The first letter denotes the 160-acre tract; the second, the 40-acre tract; and the third, the 10-acre tract. The example in Figure 3.2 shows that the well number 26 2W 22ABA means the well is in the NE 10-acre tract of the NW 40-acre tract of the NE 160-acre tract in section 22, township 26 south, range 2 west (Broeker et al., 1977, p. 2). The well number system, although very practical in the field, has two major analytical drawbacks. The location of a well is not referred to orthogonal axes, which necessitates intermediate conversions and map projection in order to convert the locations to a form suitable for standard mapping packages. Secondly, wells in the same 10-acre tract have the same well number. The problem has been partially solved for inventory purposes by adding a sequential number. For instance, the well number 26 8W 26CAB 2 means that the well is the second in the 10-acre tract 26S 8W 26CAB. The sequential number tells nothing about the location of the well within the 10-acre tract. Because of the lack of information, existing computer programs to convert well numbers to orthogonal coordinates assign the same abscissa and ordinate to all wells within the same 10-acre tract (Morgan and McNellis, 1969; Ross, 1981).
Figure 3.2--Well numbering scheme, based on the Bureau of Land Management system of land subdivision. Illustration shows location of a well whose number is 26S 2W 22ABA (after Broeker, et al., 1977, p. S).
The U. S. Geological Survey archives the information and releases an annual report containing depth to water for most of the observation wells in western Kansas, in forms such as Open-File Report 81-1001 (Pabst, 1981). Other measurements are available on request to the USGS computer files at the national headquarters in Reston, Virginia. Presently, data collection is a joint effort of the U. S. Geological Survey, the Division of Water Resources of the Kansas State Board of Agriculture, and the city of Wichita, Kansas.
Data used in the study were the latest available at the outset of the study and consist of measurements made from December 1980 to March 1981. These observations are called the "January 1981 data" because, except in special circumstances, annual measurements are scheduled to be taken during the first month of every year. The High Plains aquifer is thoroughly covered by the observation wells monitored by the U. S. Geological Survey except for the extreme northeast area around McPherson County. A few additional wells were obtained from the local Groundwater Management District No. 2 (T. C. Bell, 1981, personal letter). Table 3.1 lists the wells by file source.
Not all observation wells measured throughout the State are of interest for this study. Only 1749 of the original 2091 observation wells were included; these are listed in Appendix E.1. A total of 189 observation wells was deleted because they were in aquifers other than the High Plains aquifer (see Appendix E.2). Wells having the same coordinates cause duplicate equations in universal kriging, which results in singular matrices. Therefore, all wells except one were discarded from 10-acre tracts which contain more than one well. These wells with duplicate coordinates are listed in Appendix E.3. Wells which have no reported land surface elevation cannot be used to calculate the water table elevation. Appendix E.4 lists 40 wells that were deleted because they did not have this basic information. Finally, Appendix E.5 contains 20 wells whose depths to water were considered not to represent the true static depth, as determined by both the history of the well and the surrounding records (Pabst, 1981; M. E. Pabst, 1982, personal communication). Table 3.2 lists the number of wells in each category.
Table 3.1--Depths to water table in January 1981 observation wells listed by origin of data
| Source | No. of Wells |
|---|---|
| U. S. Geological Survey | 1988 |
| Groundwater Management District No. 2 | 103 |
| Total | 2091 |
Table 3.2--Observations that were discarded from the set of January 1981 observation well depths to water, with reason for discarding
| Category | High Plains | Other Aquifers |
|---|---|---|
| Same 10-acre tract | 93 | |
| No land surface elevation | 24 | 16 |
| Not truly static | 20 | |
| Net measurements | 1749 | 189 |
| Total | 1886 | 205 |
The present observation network for the Kansas High Plains aquifer consists primarily of the 1749 wells measured during January 1981. The exact count of wells varies from year to year as a few additional observation wells are incorporated into the system, others are dropped, and a small percent are not measured because of access problems resulting from severe weather.
The water table elevation was first analyzed to define its spatial characteristics. From the structural analysis in Appendix A, it can be seen that:
The results of the structural analysis and the 1749 water table elevations were entered into the graphics package SURFACE II (Sampson, 1978) to produce a contoured map of the surface of the water table (Plate 1) and its associated standard error (Plate 2). The aquifer boundary shown in the Plates is slightly different from the general boundary in Figure 3.1, as the Plates incorporate corrections by McClain and O'Connor (1981)and the results of detailed work done on the lithological description of the observation wells. Some of the "windows" or areas where the aquifer is missing represent local outcropping bedrock or thin, impervious parts of the aquifer which are not hydraulically connected to the main aquifer and which are not of economic interest. Crosses indicate locations of the 1749 observation wells. Figure 3.3 is a relative frequency graph based on the 5820 values in the regular grid computed by SURFACE II as an intermediate step in the preparation of the contour map. The mean of the standard errors is 12 feet (3.7 m), the standard deviation of the standard error is 4.1 feet (1.25 m), and the maximum standard error is 36.6 feet (11.2 m).
Figure 3.3--Relative frequency of the standard error of the water table elevation in the High Plains aquifer in Kansas as perceived by the present network of 1749 wells. The mean is 12 feet and the standard deviation is 4.1 feet.
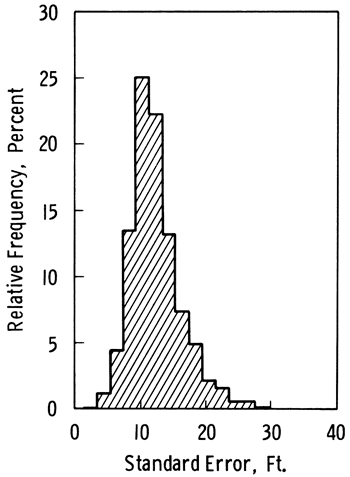
A computer program to estimate the average distance to the nearest neighbor for observations wells in the network (Olea, 1982a, Appendix B) produced a value of 2.16 miles (3.5 km). The areal extent of the aquifer is 29,000 square miles (44,000 km2), so the distance index (Appendix D) for the present network is 1.06, which is very close to the index of a random pattern. In some localities such as Harvey and Ford counties, clusters of observation wells can be clearly observed, whereas other areas are devoid of observation wells. The present network contains unsampled areas and clusters of observations, although most of the pattern is random. These patterns are not particularly efficient, as shown in Table B.1. Almost any other arrangement of observation wells would be more efficient than the pattern of the present observation network.
The present observation network in the High Plains aquifer in Kansas is justified by the need for information in order to manage exploitation of the aquifer. The network is used for both research and regulatory purposes.
The aquifer yield can be defined as the maximum rate of withdrawal that can be sustained without disturbing the system (Freeze and Cherry, 1979, p. 306). The yield of the High Plains aquifer is of intense interest, because the record obtained over more than two decades of observations in the Kansas network indicates there is a regional decline in the water table resulting from withdrawals larger than the aquifer yield.
Prediction of aquifer performance is normally done by complex numerical simulations on digital computers, in an attempt to answer questions about the effects of the number, location, and pumping rate of wells in the aquifer. Simulation programs have been improved to the stage where the accuracy of the results is limited by the amount and quality of the data supplied to the models (Foley and Dove, 1982). Water table elevation is only one of several spatial properties of an aquifer which are required as input to the models. Others include the water density, viscosity, surface tension, and compressibility; the formation porosity, permeability, and compressibility; the bedrock elevation; the aquifer boundary; and the percolation rate. Some variables such as water density are easy to measure and have a narrow range of variation. Others, such as permeability, are difficult to determine and vary suddenly over several orders of magnitude in a short distance (Delhomme, 1979). Considering the imperfect state of knowledge about these other variables, an average standard error of 12 feet (3.7 m) in the water table elevation contour maps is not a critical source of uncertainty in simulation.
A rational approach to the overall accuracy of the simulation model should involve sensitivity analysis to assess the impact of changes in the variables on the results. The number of observation wells in the network should not be increased unless it can be shown that the resulting higher precision in estimates of the water table elevation will improve the performance of hydrologic models, resulting in forecasts of increased accuracy.
Local agencies use historic records of water depth for short-range planning, such as deciding to accept or reject a request to drill a new well, a matter involving legal as well as real estate implications. The decision is influenced greatly by the water table elevation decline rate as well as by the saturated thickness in the area. The saturated thickness is the interval of permeable, porous material between the water table and the bedrock. The decline rate is the ratio of the difference in water table elevation to the duration of time over which the change occurred. Both the saturation thickness and the decline rate can be analyzed on an individual, well-by-well basis, or regionally by using contour maps.
The relevance of the estimation error of the water table elevation is increasingly critical as the saturated thickness becomes smaller and smaller. A discrepancy of 20 feet (6.1 m) does not have the same relevance where the saturated thickness is 120 feet (36.6 m)as it does where the estimated saturated thickness is only 30 feet (9.1 m). If the margins of the aquifer are of economic interest, the effectiveness of the sample design is even more important than in areas with large saturated thickness. As the present network has poor or no sampling toward the boundaries of the aquifer, a reduction of the high standard errors in these areas is a worthy goal.
Table 3.3 and Figure 3.4 show the location of 36 wells used to analyze changes in the water table decline in wells close to each other. The wells were selected in such a way that they form 18 clusters of two wells each. Throughout the aquifer, by and large, changes in water table elevation in one well in a pair have been consistently followed by a variation equal in sign and magnitude by the other well over the last 20 years. Figure 3.5 shows four typical decline curves for the wells in Finney County.
Table 3.3--Location information for wells used in decline curve correlation
| County | Well Number | Surface Elevation |
|---|---|---|
| CHEYENNE | 5S 41W 12ADC 1 | 3679.0 |
| CHEYENNE | 5S 41W 20DAA 1 | 3742.0 |
| DECATUR | 1S 29W 19BDD 1 | 2S72.0 |
| DECATUR | 1S 30W 34DDD 1 | 2610.0 |
| EDWARDS | 2SS 17W 13BCD 1 | 2107.0 |
| EDWARDS | 2SS 17W 17AAC 1 | 2129.0 |
| FINNEY | 22S 34W 26ADD 1 | 2928.0 |
| FINNEY | 22S 34W 32BCB 1 | 2983.0 |
| FINNEY | 26S 32W 3SCDA 1 | 2864.0 |
| FINNEY | 26S 33W 3DBB 1 | 2886.0 |
| HARVEY | 24S 2W 8BAA 3 | 1420.8 |
| HARVEY | 248 2W 16CBB 1 | 1413.1 |
| MEADE | 30S 29W 28BBB 1 | 27S8.0 |
| MEADE | 30S 29W 32BBB 1 | 27S6.0 |
| PRATT | 26S 13W 16DAA 1 | 1929.0 |
| PRATT | 26S 13W 19BBD 1 | 19S3.0 |
| SCOTT | 16S 34W 22BDC 1 | 3128.0 |
| SCOTT | 16S 34W 29CBB 1 | 3160.0 |
| SEDGWICK | 2SS 2W 22AAA 1 | 1386.0 |
| SEDGWICK | 2SS 2W 24DDD 3 | 1372.8 |
| SHERIDAN | 7S 29W 21ABB 1 | 2860.0 |
| SHERIDAN | 7S 29W 30ABA 1 | 2886.6 |
| SHERMAN | 9S 40W 13CDC 1 | 3722.0 |
| SHERMAN | 9S 40W 29BBB 1 | 3782.0 |
| STAFFORD | 22S 14W 29BBA 1 | 19S3.0 |
| STAFFORD | 22S 14W 3SDDB 1 | 1930.0 |
| STANTON | 30S 39W 32DA 1 | 3226.0 |
| STANTON | 30S 39W 36BDD 1 | 3181.0 |
| STEVENS | 31S 37W 9BCC 1 | 3103.0 |
| STEVENS | 31S 37W 22BCC 1 | 3096.0 |
| THOMAS | 9S 33W 30CAA 1 | 3216.0 |
| THOMAS | 9S 33W 3SAAD 1 | 314S.O |
| WALLACE | 15S 40W 3BAB 1 | 3636.0 |
| WALLACE | 15S 40W 7BBB 1 | 3706.0 |
| WICHITA | 16S 38W SBBB 1 | 3497.0 |
| WICHITA | 16S 38W 16ACC 1 | 34S2.0 |
Figure 3.4--Location of 18 clusters of two wells selected for decline curve correlation. Details are presented for wells A, B, c, and D.
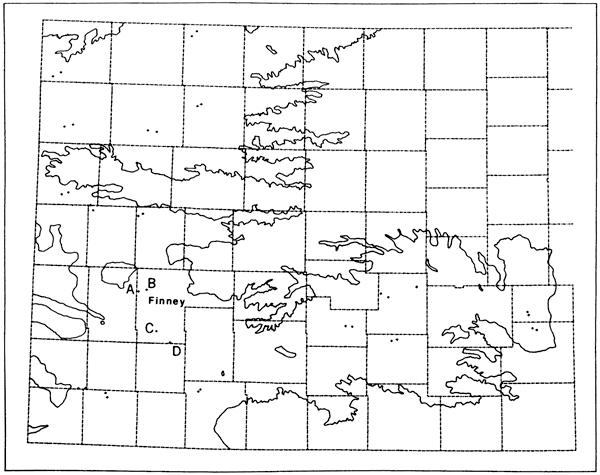
Figure 3.5--Decline curves for four wells in Finney County. Solid dots represent well A; open dots, well B; solid triangles, well C; and open triangles, well D.
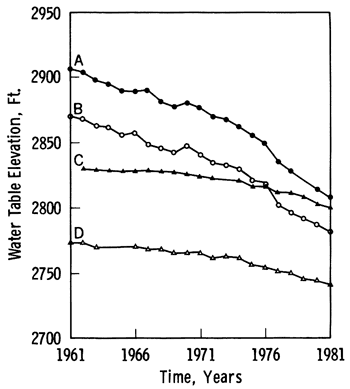
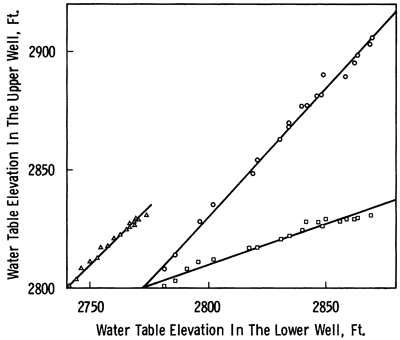
Figure 3.6 shows regressions of the elevation in well A on elevations in well B, a regression of elevations in C on elevations in D, and a regression of elevations in B on elevations in C. The results, summarized in Table 3.4, were obtained using four computer routines (Davis, 1973, programs 4-1, 4-2, 4-9, and 5-3). The almost perfect 45-degree slopes and correlations for the pairs A and B as well as C and D are clear evidence of statistical dependence between observations. Information on elevation in well B is completely redundant relative to the information gathered in well A, 4 miles (6.4 km) away. The same can be said of well D relative to C, which are as far apart as 8.6 miles (13.8 km) from each other. Other well pairs such as B and C, which are 20.8 miles (33.5 km) apart, although correlated, are sufficiently separated so as to have different rates of decline. These results suggest that, for use in the study of decline rates, the present network which has an average distance between nearest pairs of wells of only 2.16 miles (3.5 km) is unnecessarily dense.
Figure 3.6--Regressions between water table elevations in pairs of wells, for four wells in Finney County. Circles are a cross-plot of elevations in wells A and B; triangles are a cross-plot of elevations in wells C and D; and squares are a cross-plot of elevations in wells B and C. Solid lines are linear regressions.
In summary, except near the boundaries of the aquifer where too few observation wells are located, the average standard error in the network is more than adequate for the purposes of modeling and generation of decline curves.
Table 3.4--Regression on the water table elevations of four wells in Finney County.
| Wells | Distance, Miles |
Regression Line Slope |
Correlation Coefficient |
|---|---|---|---|
| A and B | 4.0 | 0.95 | 99.2% |
| C and D | 8.6 | 1.07 | 99.7% |
| B and C | 20.8 | 0.34 | 98.0% |
The systematic approach for optimally sampling spatial functions introduced in Chapter 2 is applied to improve the performance of the present groundwater network in the monitoring of water table elevation in the High Plains aquifer in Kansas presented in Chapter 3.
From the analysis in the previous chapter, it is apparent that the present network should be upgraded by optimizing the locations of observation wells. Any reallocation should be done with minimal disruption to the network. From Table B.1, the most efficient way to sample a spatial function is with a hexagonal pattern of sampling locations. Had this study been done 40 years ago, this would have been the ideal pattern of wells to use. Today, implementing a hexagonal pattern would mean retaining no more than 100 of the existing observation wells. The remainder would have to be new wells, so historical records for almost all the observation wells would be discontinued. In addition, there would have to be a significant effort in the surveying and drilling of these new wells. The potential benefit of such a severe remodeling of the network might not be justifiable. The next three patterns in Table B.1 are also regular and would have the same practical drawbacks as a hexagonal pattern. The next most effective arrangement is a stratified pattern, which is irregular and so allows the flexibility required to maximize the use of existing wells. The rearrangement which has minimum disruption of the present network is thus a stratified hexagonal pattern using existing wells.
From the discussion in the previous section, the present average standard error represents an arbitrary but convenient level of accuracy. The redesign will be done without altering the average standard error. The following constraints define what may be considered an unchanged level of the standard error throughout the aquifer.
A new network will be designed to more efficiently measure the High Plains aquifer, subject to the constraints established in part 4.1.1. As no new observation wells are included in the alternative network, it will cover only those parts of the aquifer already sampled by the present network and will not resolve the problem of unsampled areas. Thus, at this stage our attention will be concentrated on upgrading the pattern. The average standard error for the present network is 12 feet (3.7 m); 5 percent of this value is 0.6 foot (0.18 m). Over most of the contoured area shown in Plate 2, the sampling density is relatively high and the standard error is closer to 10 feet (3 m)rather than 12 feet (3.7 m). Along the margins of the aquifer, the standard error is closer to 20 feet (6.1 m), but the area is significantly smaller. The alternative network should be designed to have an average standard error somewhat lower than 12 feet (3.7 m) in most areas to compensate for higher than average standard errors in areas not sampled. Appendix C contains details for a sample design with a 10-percent penalty on the 12-feet (3.7-m) standard error which requires a density of 0.06 point/square mile (0.023 point/km2). This value can be approximately achieved by stratification in a pattern of hexagons which are 16 square miles (41.4 km2)in area. A pattern such as the one shown in Figure 4.1 was prepared which contained appropriate-sized hexagons at the one-to-one-million scale of Plate 1.
Figure 4.1--Hexagonal stratification used to randomly select one observation well inside each polygon.
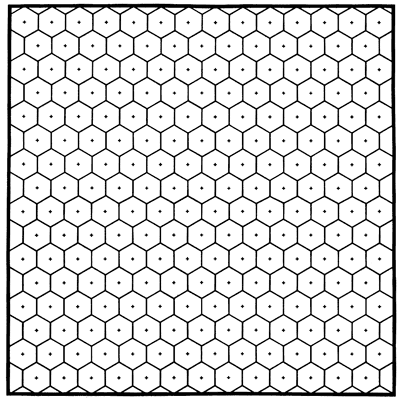
Plate 3 shows the resulting map of water table elevation using a stratified hexagonal pattern of observation wells spaced at a density of 1/16 point/square mile (0.024 point/km2). Plate 4 is the corresponding standard error map; a relative frequency graph of the standard errors appears in Figure 4.2. The alternative stratified hexagonal network retains 1135 of the 1749 observation wells shown in Plates 1 and 2. Table 4.1 compares the two networks and shows that all critical parameters are within specifications. The wells discarded from the present network are marked by an asterisk in the listing in Appendix E.1.
Figure 4.2--Relative frequency of the standard error of the water table elevation in the High Plains aquifer in Kansas as perceived by a proposed hexagonal stratified network of 1135 wells. The mean is 12.45 feet and the standard deviation is 3.75 feet.
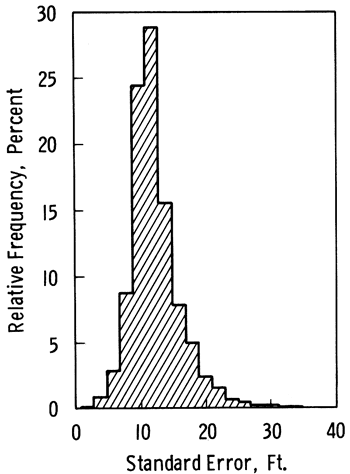
Table 4.1--Comparison between the present and alternative netowrks.
| Present | Alternative | Change | |
|---|---|---|---|
| Pattern | Random | Hex. Strat. | |
| Number of wells | 1749 | 1135 | -35.1% |
| Average standard error, feet | 12.02 | 12.45 | 3.6% |
| Nodes estimated | 5820 | 5802 | -0.3% |
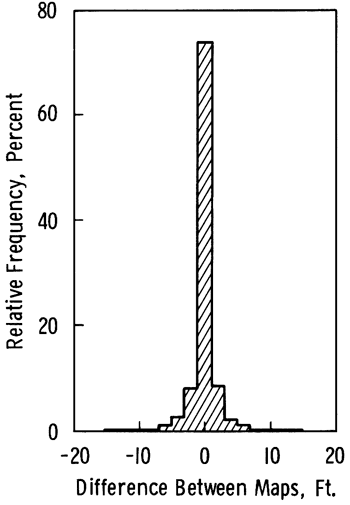
Plate 5 is an overlay of the isolines of Plates 1 and 3 and shows the difference in the perception of the water table elevation which results from modifying the network as well as the location of the discarded wells. The differences are expressed as a relative frequency graph in Figure 4.3. The maximum difference is 18.8 feet (5.7 m); 97.4 percent of estimated nodes in the alternative network are within ±5 feet (1.5 m) of the corresponding node calculated from the present network.
Figure 4.3--Differences between water table elevations estimated using the proposed network of 1135 wells and elevations estimated by present network of 1749 wells. The mean is zero and the standard deviation is 2 feet.
As all the critical parameters are within bounds, the network of 1135 wells may be an acceptable solution under the constraints in part 4.1.1. The alternative network produces an equivalent estimate of the water table elevation but uses 614 fewer observation wells than the present network. If the 137 wells in Table 3.2 that were previously discarded for reasons other than the sampling efficiency are added to these, it can be seen that the number of observation wells surveyed during January 1981 could have been reduced by almost 40 percent without impairing the worth of the network for estimating the water table.
Using a network of 1135 wells could reduce the costs of annual measurement, or the savings could be used to finance improvements in the network.
The alternative network, by using only existing wells, has the same unsampled areas as the present network. However, it would be desirable to expand the observation network so it would have a uniform density throughout the entire aquifer.
Currently, it is not possible to estimate the water table elevation for the High Plains aquifer in some areas, while in other areas the estimates are unreliable and could lead to the making of erroneous decisions. The easternmost area of the aquifer was selected to perform an experiment which shows the dangers of allowing gaps to remain in the sampling pattern.
As shown in Plate 1, the area east of range 4W has the highest density of observation wells of any area in the aquifer. This area is known as the Equus Beds. Within this region, the hexagonal stratified pattern of observation wells covers a continuous area without gaps (Plate 3). This makes the Equus Beds particularly suitable as an area in which to perform an experiment to illustrate what may happen in other places where sampling is incomplete.
Figure 4.4a shows the water table elevation, the location of observation wells, and the zone within which observation wells will be deleted to artificially create a gap in the sampling pattern. The deleted wells can be compared against the estimates generated using only the incomplete network. The differences should be equivalent to those seen in a presently unsampled area if additional observation wells were drilled. Figure 4.4b shows the water table elevation estimated using only wells outside the artificially created gap. The corresponding standard error is shown in Figure 4.4c. Four locations were selected for comparison; results are presented in Table 4.2.
Figure 4.4--Water table elevation and observation well locations in Equus Beds area. A, B, C, and D are four locations selected for comparison. Within L-shaped area indicated by dashed lines, wells are deliberately omitted from calculations. (a) Contour map based on present observation well network. (b) Contour map with wells omitted from L-shaped area. (c) Standard error of water table elevation map b. (d) Contour map based on hexagonal stratified sample of observation wells outside L-shaped area. (e) Contour map made using all available wells outside L-shaped area and a hexagonal stratified pattern of wells inside area. (f) Contour map based on a hexagonal stratified pattern having a density of one well in 16 square miles.
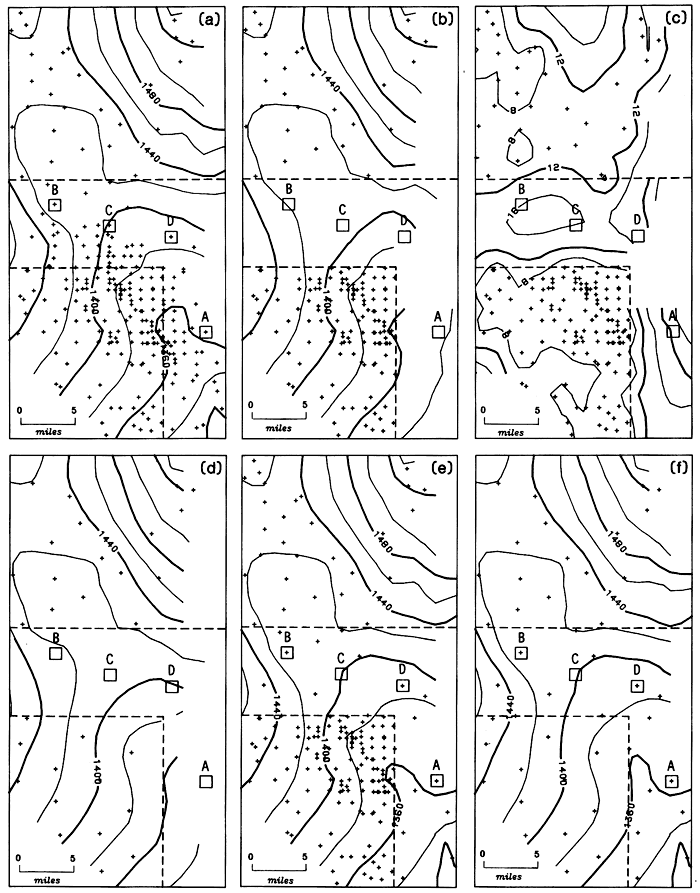
The largest errors are to the southeast. The estimated values are the result of extrapolation as all observations lie to one side of the area. The depression in the water table shown on the original map has been distorted to a southeast dipping plane. Points around location A were estimated with more than 30 feet (9.1 m) of error. Locations B and C are in the horizontal part of the strip, which is surrounded by control points in at least two directions. Because of the better control, that part of the map made with the censored data set has almost the same character as the equivalent area in the map made using the full observation well network. Only errors of detail, such as those around locations B and C, are evident. The random nature of the error is demonstrated at location D. Despite the fact that location D is no better sampled than locations B and C, the estimated value for the water table elevation does not suffer from the elimination of wells. Even though the exact amount of an error is unpredictable, the errors can at least be confined within probabilistic bounds. All errors in Table 4.2 are, for instance, within 1.5 times the standard error. The example demonstrates the advantages of analyzing the map of a spatial function with the help of a standard error map. In this way it is possible to pinpoint areas of likely significant error as well as to identify the dangerous effect of gaps in the sampling pattern.
Figure 4.4d represents the situation existing in the alternative network of 1135 observation wells after the elimination of the excess wells. The map in Figure 4.4d is essentially identical to that in Figure 4.4b. The further reduction in the number of wells outside the L-shaped strip neither worsens nor improves the uncertainties created by the sampling gap as demonstrated in Figure 4.4b.
Figures 4.4e and 4.4f illustrate the benefits of adding observations in a hexagonal stratified pattern at a density of 1/16 well per square mile (0.024 wells/km2)inside the L-shaped gap. The inserted wells restore the details evident in the original Figure 4.4a. Note that the careful placement of a few added wells in the gap can be as effective as the unplanned generous insertion of many wells, as this will result in reversion to the original situation. Figure 4.4f is the most efficient sampling pattern, a hexagonal stratified sample with no gaps at a density of 1/16 well per square mile (0.024 well/km2). Figure 4.4f represents the same solution as in Plate 3 for the Equus Beds. This experiment illustrates the benefits and advantages of extending the hexagonal stratified network to presently undersampled areas elsewhere in the aquifer.
Table 4.2--Evaluation of the effect of gaps in sampling pattern
| Location | Actual Elevation (ft.) |
Estimated Elevation (ft.) |
Difference (ft.) |
Standard Error (ft.) |
|---|---|---|---|---|
| A | 1374 | 1445 | 29 | 20 |
| B | 1402 | 1420 | 18 | 15 |
| C | 1397 | 1405 | 8 | 16 |
| D | 1390 | 1390 | 17 |
The total number of observation wells required to cover the entire aquifer with a hexagonal stratified network is 1795; that is, 660 observation wells should be measured in addition to the 1135 selected in part 4.1.2. Because there is limited interest in improving sampling in areas of marginal economics, the additional 660 wells are grouped into two categories based on the estimated saturated thickness (Bayne and Ward, 1967; O'Connor and McClain, 1981, Plates 5A and 5B). Remember that a hexagonal stratification implies the random selection of one well inside each hexagon on a regular network (Fig. B.2a). Figure 4.5 shows the location of the centers of those hexagons where additional wells are required to complete the network in areas expected to have more than 40 feet (12.2 m) of saturated thickness. There are 324 such locations. Figure 4.6 shows the centers of 336 additional hexagons in areas where the expected saturated thickness is less than 40 feet (12.2 m). Appendix F lists the locations of these 660 centers of hexagons.
Figure 4.5--Locations of the centers of 324 regular hexagons 16 square miles in size in areas where more than 40 feet of saturated thickness is expected. An observation well should be located within each hexagon.
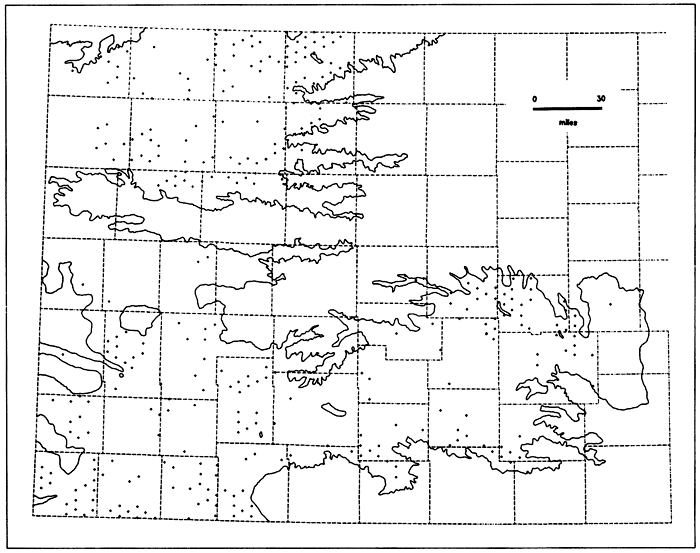
Should the entire High Plains aquifer in Kansas be sampled following these recommendations, the average standard error would be equal to the 10.8 feet (3.3 m) value obtained in Appendix C. The most dramatic changes would occur in the maximum standard error which would be reduced to 13.3 feet (4.1 m), only 36.3 percent of the present maximum standard error. Also note that the new network would contain 91 fewer observation wells than the present network as measured during January 1981. In summary, the savings generated by cutting the present network to 1135 wells could be used to finance a more exhaustive sampling of the aquifer in areas which are now insufficiently surveyed. The modified network could yield a more complete and accurate picture of the water table than does the present network.
Figure 4.6--Locations of the centers of 336 regular hexagons 16 square miles in size in areas where less than 40 feet of saturated thickness is expected. An observation well should be located within each hexagon.
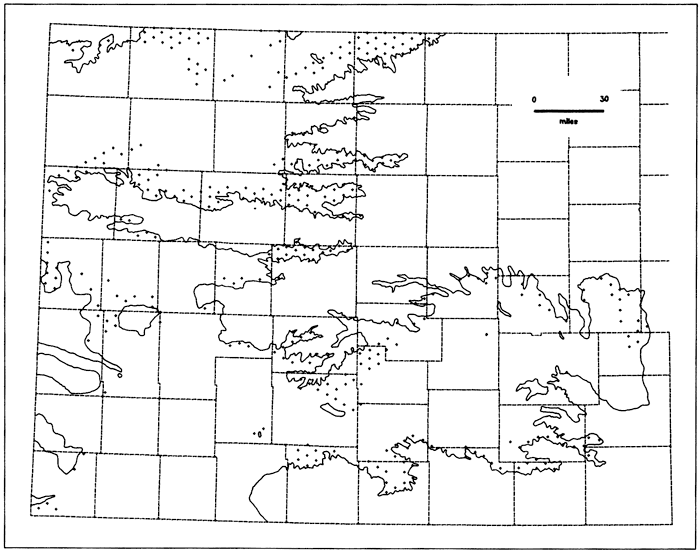
The analysis in parts of 4.1.2 and 4.2.1 is conditional on maintaining a level of accuracy similar to the present level. The advantages of changing to a hexagonal stratified pattern and expanding the network are not tied to the level of accuracy selected for the network. Other accuracy levels are certainly possible, but, as predicted by Equation 2.4, producing a radical change in the standard error throughout the aquifer will require a substantial change in the number of observation wells.
Figure 4.7 shows the changes in total number of wells required to uniformly vary the accuracy throughout the aquifer if a hexagonal stratified pattern is used. From part 4.2.1, 1795 observation wells would be required to produce an average standard error of 10.8 feet (3.3 m) for the water table elevation of the High Plains aquifer in Kansas. Due to the parabolic nature of the relationship between standard error and density, the marginal return on changes in either direction is not favorable. As the curve flattens to the right, reducing the number of wells will cause significant increases in the standard error. The converse is true if the number of wells is increased. The curve rises sharply to the left and the addition of significant numbers of wells will cause only minor reductions in the standard error. For example, keeping the density uniform, a reduction of 1000 wells from the network would increase the standard error by 22.5 percent, but increasing the density by adding 1000 more wells would only reduce the standard error by 10.5 percent.
Figure 4.7--Network size as a function of level of accuracy in the estimation of water table elevations in the High Plains aquifer in Kansas. Sampling is assumed to follow a hexagonal stratification.
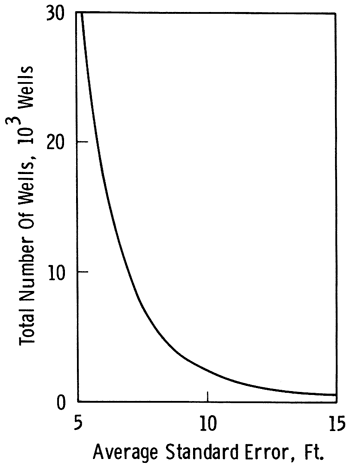
In summary, if the sampling pattern is kept constant, the sampling efficiency indices can be modified by changing the density of observations. The rate of deterioration caused by reducing the sample size is higher than the rate of improvement produced by increasing the sample size by the same amount.
The purpose of this study has been to analyze the sampling efficiency of the observation well network used to monitor water table elevations in the High Plains aquifer in Kansas and to propose modifications that will enhance the network. The conclusions and recommendations of this investigation are best expressed through consideration of each of the specific objectives of the study.
This study of the Kansas High Plains aquifer network is based on information gathered during the period December 1980 to March 1981, consisting of measurements of depth to the water table in 1886 observation wells. The water table elevations contain a spatial drift which can be modeled by a first-degree polynomial of the geographic coordinates. The semivariance of the residuals can be represented by a linear semivariogram having a slope of 60 feet2 per mile (3.5 m2/km)within a neighborhood which is 28 miles (45 km)in diameter.
The observation wells are concentrated in areas which include about three-fourths of the aquifer in Kansas. Undersampled areas occur mostly near the aquifer's boundaries. There are some local clusters of wells. Overall, the network has a distance index of 1.06, indicating that the observation wells are distributed essentially at random. The water table elevation can be estimated with an average standard error of 12 feet (3.7 m)and a maximum standard error of 36.6 feet (11.2 m)using the 1749 wells which have acceptable measurements.
Information gathered by the network is used primarily as input to hydrologic models and to assist groundwater managers in planning the exploitation of the aquifer. Prediction of aquifer performance is normally done by complex numerical simulations on digital computers in an attempt to answer questions about the effects of the number, location, and pumping rate of wells. The process is complemented by information on water saturation and decline rate prepared from the same basic data.
The observation wells are spaced sufficiently close and the average standard error of the water table elevation associated with the present observation network is sufficiently low to satisfactorily fulfill all the requirements placed on data gathered by the network. The network is adequate for determining the location of new irrigation wells and the error of estimation is much smaller than the relative average standard error of other variables used in hydrologic modeling. If a decision is made to invest more money in surveys of the High Plains aquifer in Kansas, these additional funds should be directed to improving the accuracy of other variables required for hydrologic modeling, rather than attempting to reduce the average standard error of the water table elevation. A substantial reduction in average standard error cannot be easily achieved. Because of the parabolic nature of the change in standard error with well density, 16 times as many wells would be required to reduce the present average standard error by one-half. However, areas of low sampling, particularly near the edges of the aquifer, result in a maximum standard error which could be substantially reduced by reallocating wells from areas that presently are oversampled.
The present observation well network should be modified to be more efficient. That part of the aquifer already covered by the network should be redesigned, maintaining the same level of average error as the present network. A stratified pattern of observation wells is recommended because this will allow enhancement of the network utilizing existing observation wells, thus minimizing disruption in the historical records and requiring no additional surveying or drilling. Application of the systematic sampling procedure contained in Algorithm 2.1 to the High Plains aquifer produces a stratified pattern of wells spaced within hexagonal areas containing 16 square miles (41.4 km2). Contour maps of the water table elevation can then be produced with no deterioration in the quality of the estimates using only eight nearest neighbors. li the present network is modified following these recommendations, the new network would contain only 1135 observation wells, a reduction of 39.8 percent in the number of wells which must be measured each year. This reduction in network size would produce only a 3.6 percent increase in the average standard error. The difference between water table elevation contour maps produced by the present and the proposed networks is less than 5 feet (1.5 m) at 97.4 percent of the grid nodes and in no case is greater than 18.8 feet (5.7 m). This difference is less than a single contour interval on maps typically used to show the water table elevation in the High Plains aquifer.
The savings generated by reducing the size of the network could be used to operate the network at a lower cost or to expand the sampled region, providing measurements in areas where presently there are no observation wells. A total of 324 observation wells should be added to the 1135 wells in the alternative observation network, to assure complete coverage of all areas of the aquifer expected to have 40 feet (12.2 m)or more of saturated thickness. An additional 336 wells would be required to completely cover the High Plains aquifer everywhere in the State of Kansas at a uniform density of one well in every 16-square-mile (41.4 km2)regular hexagon. Elimination of unsampled areas would reduce the maximum standard error to 13.3 feet (4.1 m), significantly below the 36.6 feet (11.2 m) value for the current network. The 1795 wells required for the expanded network still would be 91 wells fewer than the number of observation wells actually measured in January 1981.
Armstrong, M., and R. Jabin, 1981, Variogram models must be positive-definite: Journal of the International Association for Mathematical Geology, vol. 13, no. 5, p. 455-459.
Bayne, C. K., and J. R. Ward, 1967, Saturated thickness and specific yield of cenozoic deposits in Kansas: Kansas Geological Survey, Map M-5, 1 sheet, scale 1:500,000
Broeker, M. E., H. J. Mcintyre, Jr., and J. M. McNellis, 1977, Ground-water levels in observation wells in Kansas, 1971-1975: Kansas Geological Survey, Basic Data Series, Ground-water Release 6, 526 p.
Clark, I., 1979, Practical Geostatistics: Applied Science Publishers Ltd., London, England, 129 p.
Clark, P. J., and R. C. Evans, 1954, Distance to nearest neighbors as a measure of spatial relationships in populations: Ecology, vol. 35, no. 4, p. 445-453.
David, M., 1977, Geostatistical Ore Reserve Estimation: Elsevier Scientific Publishing Company, Amsterdam, The Netherlands, 364 p.
Davis, J. C., 1973, Statistics and Data Analysis in Geology: John Wiley & Sons, Inc., New York, N.Y., 550 p.
Delhomme, J. P., 1979, Spatial variability and uncertainty in groundwater flow parameters: A geostatistical approach: Water Resources Research, vol. 15, no. 2, p. 269-280.
Foley, M.G., and F.H. Dove, 1982, Hydrology: Geotimes, vol. 27, no. 2, p. 40-41.
Freeze, R. A., and J. A. Cherry, 1979, Groundwater: N.J., 604 p. Prentice-Hall, Inc., Englewood Cliffs,
Gutentag, E. D., and J. B. Weeks, 1980, Water table in the High Plains aquifer in 1978 in parts of Colorado, Kansas, Nebraska, New Mexico, Oklahoma, South Dakota, Texas and Wyoming: U. S. Geological Survey, Open-File Report 80-50, 1 Plate.
Hogg, R. V., and Craig, A. T., 1970, Introduction to Mathematical Statistics: The Macmillan Company, New York, N.Y., 415 p.
James, G., and R. C. James, 1976, Mathematics Dictionary: Van Nostrand Reinhold Company, New York, N.Y., 509 p.
Journel, A. G., and C. J. Huijbregts, 1978, Mining Geostatistics: Academic Press, London, England, 600 p.
Kendall, M.G., and W. R. Buckland, 1971, A Dictionary of Statistical Terms: Oliver & Boyd, Edinburgh, Scotland, 166 p.
Matérn, B., 1960, Spatial variation: Meddelanden från Statens Skogsforskningsinstitut, Stockholm, vol. 49, no. 5, p. 1-144.
Matheron, G., 1965, Les variables régionalisees et leur estimation: Masson et Cie, Editeurs, Paris, France, 305 p.
Matheron, G., 1971, The theory of regionalized variables and its applications: Les Cahiers du Centre de Morphologie Mathématique, Ecole Nationale Supérieure des Mines, Paris, France, 211 p.
Morgan, C. O., and J. M. McNellis, 1969, FORTRAN IV program, KANS, for conversion of General Land Office locations to latitude and longitude coordinates: Kansas Geological Survey, Special Distribution Publication 42, 24 p.
O'Connor, H. G., and T. J. McClain, 1981, Geologic and hydrologic characteristics of the Ogallala and peripheral aquifers in western Kansas: Kansas Geological Survey, Internal Distribution Publication, University of Kansas, Lawrence, Kansas, 103 p.
Olea, R. A., 1975, Optimum mapping techniques using regionalized variable theory: Kansas Geological Survey, Series on Spatial Analysis No. 2, 137 p.
Olea, R. A., 1977, Measuring spatial dependence with semivariograms: Kansas Geological Survey, Series on Spatial Analysis No. 3, 29 p.
Olea, R. A., 1982a, Systematic approach to sampling of spatial functions: D.E. dissertation, Chemical and Petroleum Engineering Department, University of Kansas, Lawrence, Kansas, 277 p.
Olea, R. A., 1982b, Systematic sampling of spatial functions: Kansas Geological Survey, Series on Spatial Analysis No. 8, in preparation.
Pabst, M. E., 1981, January 1981 water levels, and data related to the water level changes, western and south-central Kansas: U. S. Geological Survey, Open-File Report 81-1001, 168 p.
Ripley, B. D., 1981, Spatial Analysis: John Wiley & Sons, New York, N.Y., 252 p.
Ross, C. G., 1981, GIMMAP: Geodata Interactive Management Map Analysis and Production: M.S. thesis, Computer Science Department, University of Kansas, Lawrence, Kansas, 231 p.
Sampson, R. J., 1978, SURFACE II graphics system: Kansas Geological Survey Series on Spatial Analysis No. 1, 240 p.
U. S. Geological Survey, 1980, Project document for Kansas Geological Survey, Ground-water level data: U. S. Geological Survey, Report KS00-002, 12 p.
Williams, W. H., 1978, A Sampler on Sampling: John Wiley & Sons, New York, N.Y., 254 p.
Kansas Geological Survey, High Plains Aquifer Observation Network
Placed on web June 23, 2012; originally published in 1982.
Comments to webadmin@kgs.ku.edu
The URL for this page is http://www.kgs.ku.edu/Publications/Bulletins/GW7/index.html