Kansas Geological Survey, Ground Water Series 7, originally published in 1982
Prev Page--Start of Report ||
Next Page--Data Listings
The semivariance y(![]() ) can be plotted against values of the lag
) can be plotted against values of the lag ![]() to yield the semivariogram, a graph analogous to the correlogram used in time series analysis. Structural analysis is the term applied to the study of semivariograms for the purpose of extracting information about the nature of fluctuation in a regionalized variable. The objectives of structural analysis are two-fold; to make genetic interpretations about the regionalized variable, and to provide parameters which are required in its estimation.
to yield the semivariogram, a graph analogous to the correlogram used in time series analysis. Structural analysis is the term applied to the study of semivariograms for the purpose of extracting information about the nature of fluctuation in a regionalized variable. The objectives of structural analysis are two-fold; to make genetic interpretations about the regionalized variable, and to provide parameters which are required in its estimation.
To obtain a semivariogram, it is necessary to sample the regionalized variable at regular intervals. Let
z(![]() 1), z
1), z![]() 2), ..., z(
2), ..., z(![]() i), ..., z(
i), ..., z(![]() n)
n)
be n values of either residuals or outcomes of the regionalized variable. Provided that the regionalized variable is first-order stationary and the intrinsic hypothesis holds, the following is an unbiased estimator of the semivariance (Olea, 1977, p. 20):
γ*(![]() ) = 1/(k-p) ∑j=k'k'+k-p-1 [z(
) = 1/(k-p) ∑j=k'k'+k-p-1 [z(![]() j+
j+![]() ) - z(
) - z(![]() j)]2 (A.1)
j)]2 (A.1)
Here, ![]() is p times the sampling interval
is p times the sampling interval ![]() ; k + k' ≤ n; and p = 0, 1, 2, ..., k-1. The study may be done along one traverse or, more desirably, along a series of traverses. The estimation of a semivariogram for observations of a regionalized variable is fairly straightforward, but this is not true for the semivariogram of the residuals. Before the residuals can be obtained, it is necessary to know the semivariogram. The problem is solved recursively by assuming a semivariogram, computing the drift and residuals, and comparing the resulting semivariogram to that assumed (Olea, 1975, p. 90-93; David, 1977, p. 272-274).
; k + k' ≤ n; and p = 0, 1, 2, ..., k-1. The study may be done along one traverse or, more desirably, along a series of traverses. The estimation of a semivariogram for observations of a regionalized variable is fairly straightforward, but this is not true for the semivariogram of the residuals. Before the residuals can be obtained, it is necessary to know the semivariogram. The problem is solved recursively by assuming a semivariogram, computing the drift and residuals, and comparing the resulting semivariogram to that assumed (Olea, 1975, p. 90-93; David, 1977, p. 272-274).
Satisfactory results for moderately tractable regionalized variables can be obtained by assuming drifts of the type
M*(![]() ) = ∑ni=0aifi(
) = ∑ni=0aifi(![]() ) (A.2)
) (A.2)
where the ai are n unknown coefficients to be determined and the fi(![]() ) are functions of
) are functions of ![]() , typically monomials of the spatial coordinates up to degree 2. The smooth and slowly varying surfaces represented by M*(
, typically monomials of the spatial coordinates up to degree 2. The smooth and slowly varying surfaces represented by M*(![]() ) accord with the mathematical notion of the drift being a highly continuous function incorporating only the low frequency component of the regionalized variable without the local fluctuations. The terms local and regional are relative and depend upon the scale of the regionalized variable. A feature that at the scale of a county could be a dominant element in the drift could be an anomaly when considering an entire state, and could be completely negligible at a continental scale. Therefore, there is no single, unique drift for a given regionalized variable; as in curve fitting, the user must decide what should be fitted and what should be regarded as anomalous.
) accord with the mathematical notion of the drift being a highly continuous function incorporating only the low frequency component of the regionalized variable without the local fluctuations. The terms local and regional are relative and depend upon the scale of the regionalized variable. A feature that at the scale of a county could be a dominant element in the drift could be an anomaly when considering an entire state, and could be completely negligible at a continental scale. Therefore, there is no single, unique drift for a given regionalized variable; as in curve fitting, the user must decide what should be fitted and what should be regarded as anomalous.
Certain major characteristics of the regionalized variable of interest in this study can be deduced from the semivariogram. These include:
1. Continuity. The shape of the semivariogram, and in particular its slope near the origin, is related to the regularity and smoothness of the regionalized variable. A parabolic semivariogram which is tangent to the x-axis at the origin means the variable is extraordinarily regular relative to the sampling interval. In contrast, highly erratic sequences will produce a semivariogram which is almost vertical at the origin.
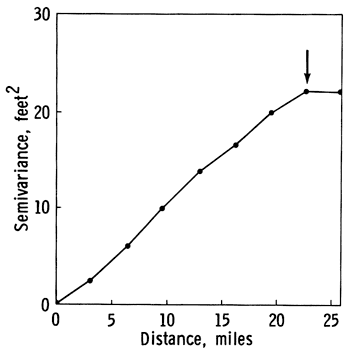
2. Zone of influence. Figure A.1 is a transitive type of semivariogram, expressing moderate continuity of the regionalized variable within a local neighborhood, and random behavior over larger distances. The semivariance steadily increases to a maximum value and then remains constant at a value called the sill. In instances where the regionalized variable is second-order stationary, the asymptote is equal to the sample variance (Olea, 1982a, p. 15). The arrow at the slope break indicates the range, a distance which divides elements in a sample into two categories. Samples taken at distances which are smaller than the range are autocorrelated and are ideally suited to be used in common for estimation purposes. Samples spaced further apart than the range are statistically independent and behave as independent random variables.
Figure A.1--Transitive type semivariogram with a range of 22.5 miles.
3. Anisotropy. Anisotropy is revealed by different behavior of the semivariograms computed along lines having different orientations. The differences in the semivariogram appear mainly in the slope at the origin, in the range, and in the sill, if any. The semivariance of a regionalized variable could be anisotropic and at the same time the semivariance of the residuals could be isotropic, if the cause of the anisotropy is an underlying drift. This situation can be diagnosed if along the dip the semivariogram is highly regular with no sill and along the strike the semivariogram is transitive in form. If the regionalized variable is isotropic, the semivariance depends only on the magnitude h of the vector ![]() and not on the direction
and not on the direction ![]() .
.
Although any function that fits the observed semivariance could be used as a model, sound geostatistical practice recommends the use of only those functions which are positive-definite (Journel and Huijbregts, 1978, p. 161-168; Armstrong and Jabin, 1981). Among the positive_ definite models, the simplest one is linear:
γ(![]() ) = ω(
) = ω(![]() ) (A.3)
) (A.3)
The linear model is a convenient choice to represent a transitive semivariogram provided the argument ![]() never becomes larger than the range. That is, the estimators are restricted to sample subsets inside the zone of influence.
never becomes larger than the range. That is, the estimators are restricted to sample subsets inside the zone of influence.
When the model must incorporate the presence of a sill, the most commonly used function is the spherical model
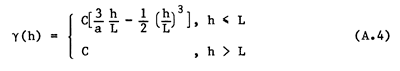
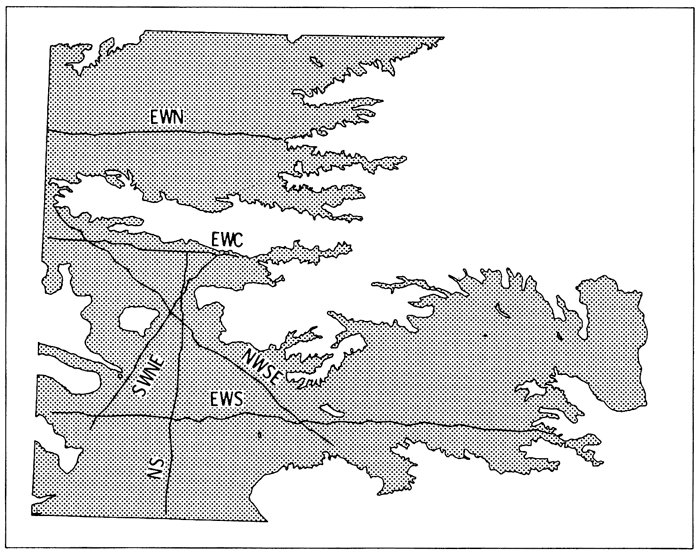
Ideally, the semivariogram should be estimated along regularly sampled traverses of the regionalized variable. These traverses should run in at least three different orientations and should contain a minimum of about 30 sample elements (Journel and Huijbregts, 1978, p. 194). In circumstances such as the measurement of water table elevation in the High Plains aquifer of Kansas, these ideal conditions cannot be met because the samples have already been taken at irregularly spaced locations. Some sampling approximations are allowable, however, such as minor changes in orientation along the traverses, interpolation of a few missing points, and small variations in the spacing (Clark, 1979, p. 118-119). Figure A.2 shows the traverses selected through the well locations given in Appendix E.1 which best fulfill the ideal requirements. These six traverses run in four different orientations approximately 45 degrees apart.
Figure A.2--Locations of traverses used in structural analyses.
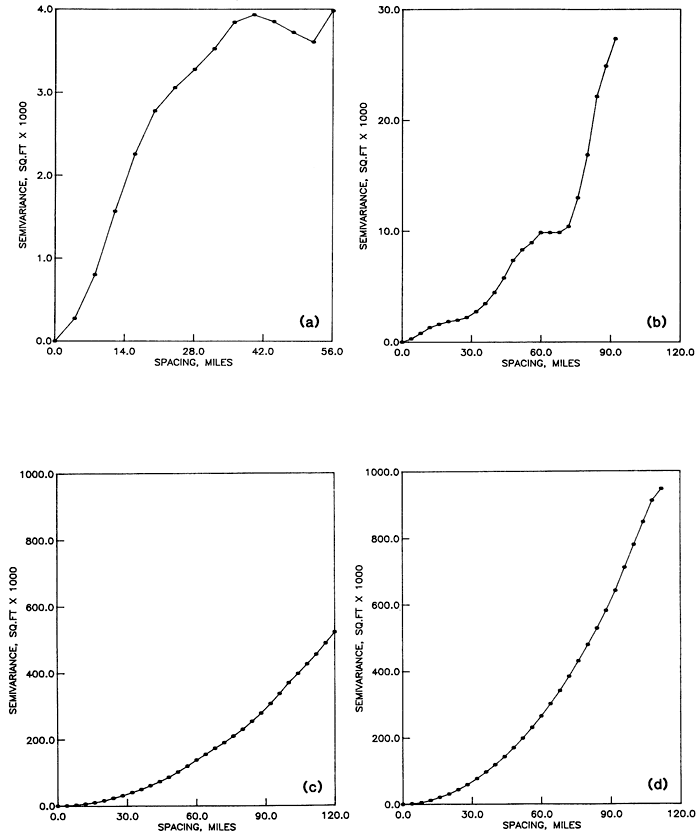
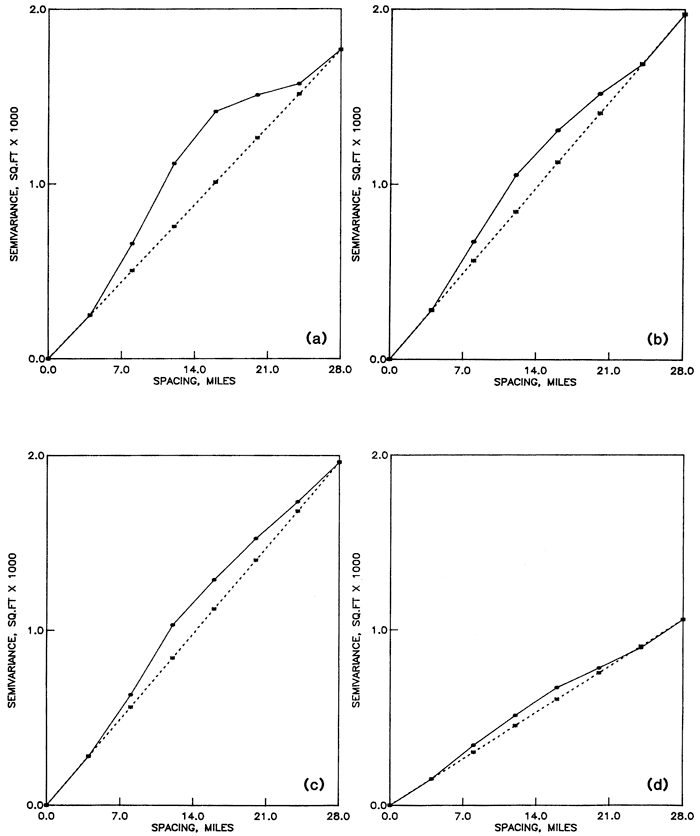
Structural analysis was performed using the program SEMIVAR (Olea, 1977). In general the water table elevation dips east with a slope of 8 feet per mile (3.9 m/km), meaning that, except along the north-south strike, the assumption of stationarity required by the semivariance estimator in Equation A.1 is not met. This is revealed by the anisotropy shown in the semivariograms of Figure A.3. The semivariogram for traverse NS in Figure A.3a is transitive. From the discussion in the previous part A.1, its range is approximately 28 miles (45 km). On the other hand, traverse NWSE (Fig. A.3c) does not possess a sill but rather is a monotonically increasing semivariogram tangent to the x-axis at the origin. Because of the lack of stationarity in the drift, we must seek the semivariance of the residuals.
Figure A.3--Semivariances of water table elevations along traverses across the High Plains aquifer. (a) Semivariance along traverse NS. (b) Semivariance along traverse SWNE. (c) Semivariance along traverse NWSE. (d) Average semivariance for east-west traverses.
Estimation of the semivariance of the residuals is an undetermined problem, because the calculation of residuals requires computation of the drift, and estimation of the drift presumes knowledge of the semivariance. The problem is solved recursively by assuming a semivariogram, computing the drift, estimating the residuals, and comparing the semivariogram for these residuals with the initially assumed semivariance.
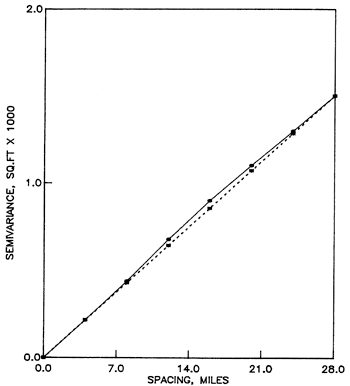
The simplest starting model is a linear semivariogram, whose drift is not a function of the slope ω (Olea, 1975, p. 54). Therefore, the estimated semivariogram is invariant under a change of assumed slope. Rather than estimating the assumed slope by a regression line through the estimated semivariogram, the practice is to make that slope equal to the slope at the origin in the estimated semivariogram. The justification for this practice is the fact that the reliability of the estimated semivariance decreases as the argument increases, primarily because of the decreasing number of pairs in Equation A.1 as the distance between sample elements increases (Clark, 1979, p. 18; Journel and Huijbregts, 1978, p. 193). However, the analysis will depend on what portion of the semivariance is modeled. A linear model will perform well only for arguments no larger than the range. From Figure A.3, analysis should be confined to arguments no larger than 28 miles (45 km). Polynomials of degree one and two were selected as drifts. Figures A.4 to A.7 show the results of the structural analysis which are also expressed in condensed form in Table A.1.Table A.1--Semivariogram slopes for linear models.
| Traverse | Length (mi.) |
Degree of Drift Polynomial | |||
|---|---|---|---|---|---|
| 0 | 1 | 2 | |||
| NS | 121 | 71 | 65 | 46 | |
| SWNE | 92 | 76 | 70 | 63 | |
| NWSE | 156 | 217 | 70 | 58 | |
| EWN | 112 | 343 | 38 | 39 | |
| EWC | 94 | 233 | 36 | 38 | |
| EWS | 224 | 193 | 64 | 65 | |
| Average | 177 | 59 | 54 | ||
Figure A.4--Semivariances of residuals from a first-degree polynomial drift of water table elevations in the High Plains aquifer. (a) Semivariance of residuals along traverse NS. (b) Semivariance of residuals along traverse SWNE. (c) Semivariance of residuals along traverse NWSE. (d) Average semivariance of residuals along east-west traverses.
The discrepancy among the traverses is substantially reduced by subtracting the drift, but regardless of the type of drift, the assumed and experimental semivariograms are different. Based on the results for the east-west traverses, the remaining discrepancy is considered to be within the statistical variation of the estimates and should be cancelled out by averaging all traverses. For some traverses, a second-degree polynomial drift model provides slightly better results in terms of removing the aniotropy and fitting the estimated semivariogram to the assumed semivariogram. However, the improvement is not that dramatic so as to change the geological notion that the drift of the water elevation is a plane.
For the purpose of this study, the following is considered a satisfactory model for the semivariance of the residuals
γ(h) = 60 h (A.5)
for arguments no larger than 28 miles (45 km). This value is sufficiently large that it is not necessary to extend the analysis to models valid for larger arguments which include the presence of a sill.
Figure A.5--Average semivariance of residuals from a first-degree polynomial drift for all traverses.
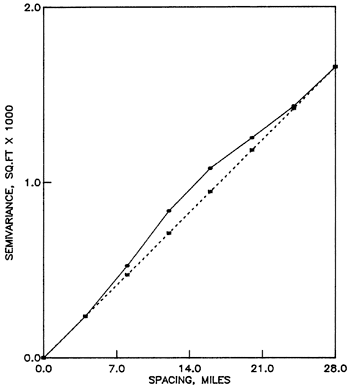
Figure A.6. Semivariances of residuals from a second-degree polynomial drift of water table elevations in the High Plains aquifer. (a) Semivariance of residuals along traverse NS. (b) Semivariance of residuals along traverse SWNE. (c) Semivariance of residuals along traverse NWSE. (d) Average semivariance of residuals along east-west traverses.
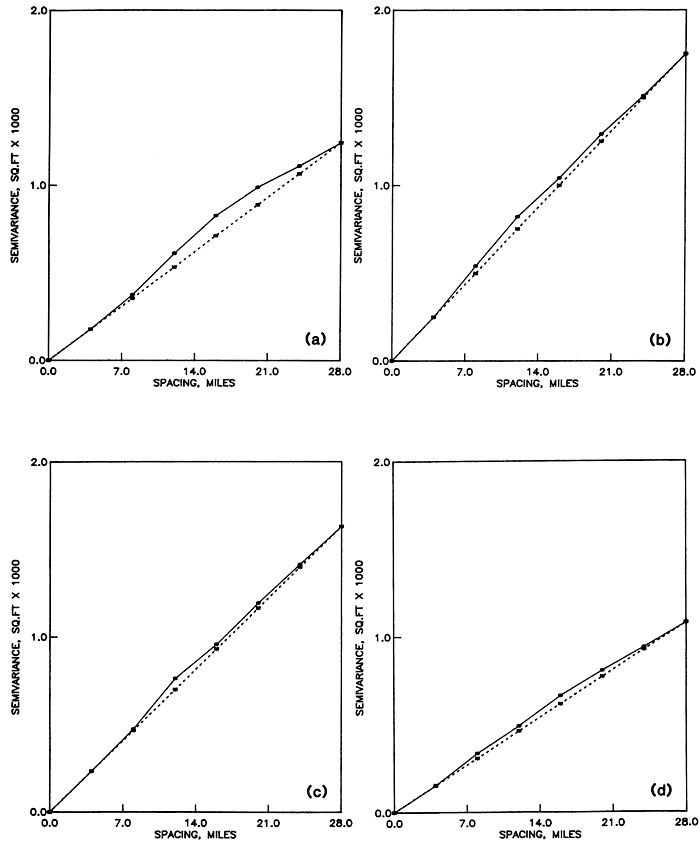
Figure A.7--Average semivariance of residuals from a second-degree polynomial drift for all traverses.
Pattern is a nominal variable which refers to different configurations of objects, which in this case are the sample elements or observation well locations. A pattern involves distances among the elements in the set, here arranged in two dimensions. Some patterns have unique characterizations; for example, there is only one way to arrange elements in a square pattern. All square patterns are the result of scaling, rotation, or translation of the one basic type. In contrast, a random pattern has only a statistical definition, as there are an infinite number of possible configurations that fit the description of randomness.
Utility computer programs were prepared to generate sample element patterns covering the entire range of possible patterns (Olea, 1982a, Appendix B). From these, 14 patterns grouped into 7 categories were selected, as shown in Figure B.1.
Figure B.1--Sample element patterns investigated in this study. Patterns (a) through (c) are regular, (d) and (e) consist of orthogonal regular traverses, (f) and (g) are stratified, (h) is a random pattern, (i) and (j) are bisymmetrical, and (k) through (n) are clustered patterns.
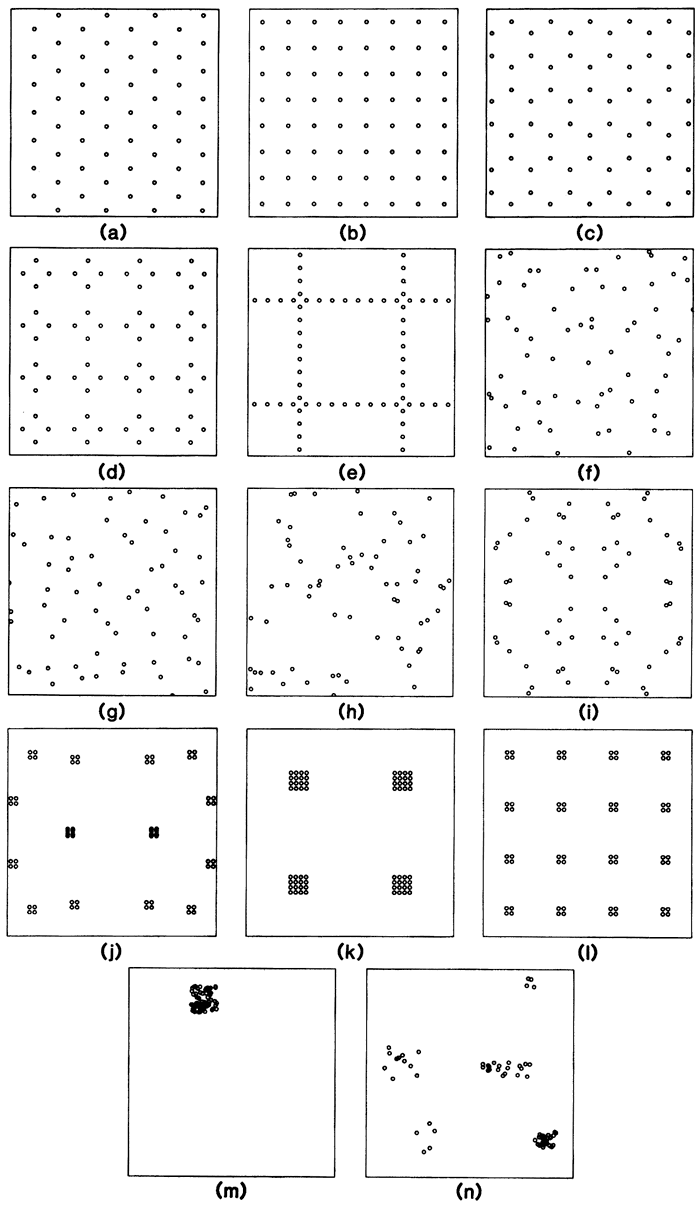
Categories 1 and 2 are uniquely defined. The remaining patterns are representative examples from among an infinite set of possibilities. It can be proven that the three patterns shown as Figure B.1a-c are the only regular configurations which can be formed in a two-dimensional space (Matern, 1960, p. 74).
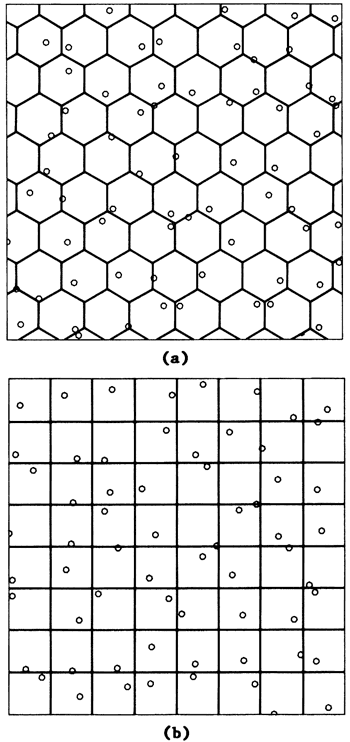
Stratified sampling is a selection procedure in which the sample space is divided into mutually exclusive partitions and an element is then randomly taken from every partition (Ripley, 1981, p. 19-22). Figure B.2 illustrates stratified sampling of a two-dimensional space partitioned into squares and into hexagons. The randomly selected points are the same as in Figure B.1f and B.1g.
Figure B.2-- Sampling mechanism for stratified patterns. (a) One point is selected randomly from inside each hexagon. (b)One point is selected randomly from inside each square.
The following tables contain values of average standard error and maximum standard error assuming the sample elements and the estimated value have the same support. The sampling density is one point per square mile (0.39 point/km2)and the semivariogram is linear with unit slope.
Table B.1--Sampling efficiency indices at unit linear semivariogram slope, unit density, and 32 nearest neighbors.
| Pattern | Average Std. Error Drift |
Maximum Std. Error Drift |
||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 0 | 1 | 2 | |
| Hexagonal | 0.63 | 0.63 | 0.63 | 0.72 | 0.72 | 0.72 |
| Square | 0.64 | 0.64 | 0.64 | 0.74 | 0.74 | 0.74 |
| Triangular | 0.66 | 0.66 | 0.66 | 0.80 | 0.80 | 0.80 |
| Traverses every 2 points |
0.68 | 0.68 | 0.68 | 0.89 | 0.89 | 0.89 |
| Hexagonal stratification |
0.69 | 0.69 | 0.69 | 0.86 | 0.86 | 0.86 |
| Square stratification |
0.69 | 0.69 | 0.69 | 0.91 | 0.91 | 0.91 |
| Random | 0.71 | 0.71 | 0.71 | 1.05 | 1.05 | 1.05 |
| Bisymmetrical random |
0.72 | 0.72 | 0.72 | 0.98 | 0.98 | 0.98 |
| Traverses every 8 points |
0.81 | 0.81 | 0.84 | 1.23 | 1.23 | 1.45 |
| Four points per regular cluster |
0.83 | 0.83 | 0.84 | 0.99 | 0.99 | 1.00 |
| Five clusters | 0.98 | 0.99 | 1.06 | 1.33 | 1.49 | 2.33 |
| Bisymmetrical clusters |
1.03 | 1.03 | 1.11 | 1.22 | 1.22 | 1.38 |
| Sixteen points per regular cluster |
1.13 | 1.17 | 1.53 | 1.51 | 1.85 | 5.13 |
| One cluster | 2.19 | 5.01 | 61.50 | 2.94 | 8.27 | 148.00 |
Table B.2--Points of no additional return on sampling efficiency indices by increasing the number of nearest neighbors
| Pattern | Average Std. Error Drift |
Maximum Std. Error Drift |
||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 0 | 1 | 2 | |
| Hexagonal | 3 | 5 | 10 | 3 | 5 | 10 |
| Square | 4 | 5 | 10 | 10 | 10 | 14 |
| Triangular | 8 | 8 | 11 | 11 | 12 | 12 |
| Traverses every 2 points |
12 | 12 | 20 | 14 | 15 | 26 |
| Hexagonal stratification |
6 | 6 | 16 | 7 | 8 | 25 |
| Square stratification |
8 | 8 | 18 | 10 | 11 | 30 |
| Random | 12 | 12 | 32+ | 12 | 14 | 32 |
| Bisymmetrical random |
8 | 8 | 32+ | 20 | 28 | 32 |
| Traverses every 8 points |
28 | 32+ | 32+ | 28 | 32+ | 32 |
| Four points per regular cluster |
12 | 12 | 32+ | 22 | 28 | 32 |
| Five clusters | 32+ | 32+ | 32+ | 32+ | 32+ | 32 |
| Bisymmetrical clusters |
20 | 20 | 32+ | 26 | 28 | 32 |
| Sixteen points per regular cluster |
32+ | 32+ | 32+ | 32+ | 32+ | 32 |
| One cluster | 32+ | 32+ | 32+ | 32+ | 32+ | 32 |
Table B.3--Minimum number of nearest neighbors required to solve the universal kriging system of equations
| Pattern | Drift | ||
|---|---|---|---|
| 0 | 1 | 2 | |
| Hexagonal | 1 | 3 | 6 |
| Square | 1 | 3 | 7 |
| Triangular | 1 | 3 | 7 |
| Traverses every 2 points |
1 | 3 | 9 |
| Hexagonal stratification |
1 | 3 | 6 |
| Square stratification |
1 | 3 | 6 |
| Random | 1 | 3 | 6 |
| Bisymmetrical random |
1 | 3 | 9 |
| Traverses every 8 points |
1 | 5 | 9 |
| Four points per regular cluster |
1 | 3 | 9 |
| Five clusters | 1 | 3 | 6 |
| Bisymmetrical clusters |
1 | 5 | 12 |
| Sixteen points per regular cluster |
1 | 5 | 9 |
| One cluster | 1 | 3 | 7 |
Table B.4--Average standard error the drift is a constant unit density and unit linear semivariogram slope
| Pattern | Number of nearest neighbors | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 6 | 8 | 12 | 16 | 32 | |
| Hexagonal | 0.83 | 0.67 | 0.63 | 0.63 | 0.63 | 0.63 | 0.63 | 0.63 | 0.63 |
| Square | 0.86 | 0.68 | 0.65 | 0.64 | 0.64 | 0.64 | 0.64 | 0.64 | 0.64 |
| Triangular | 0.88 | 0.74 | 0.69 | 0.68 | 0.67 | 0.66 | 0.66 | 0.66 | 0.66 |
| Orthogonal traverses every 2 points |
0.92 | 0.78 | 0.73 | 0.71 | 0.70 | 0.69 | 0.69 | 0.68 | 0.68 |
| Hexagonal stratification |
0.90 | 0.76 | 0.72 | 0.70 | 0.69 | 0.69 | 0.69 | 0.69 | 0.69 |
| Square stratification |
0.90 | 0.78 | 0.72 | 0.71 | 0.70 | 0.69 | 0.69 | 0.69 | 0.69 |
| Random | 0.93 | 0.82 | 0.78 | 0.76 | 0.73 | 0.72 | 0.72 | 0.71 | 0.71 |
| Bisymmetrical random |
0.95 | 0.82 | 0.78 | 0.75 | 0.73 | 0.72 | 0.72 | 0.72 | 0.72 |
| Orthogonal traverses every 8 points |
1.08 | 0.99 | 0.95 | 0.93 | 0.88 | 0.86 | 0.84 | 0.83 | 0.81 |
| Four points per regular cluster |
1.11 | 1.03 | 0.99 | 0.97 | 0.87 | 0.86 | 0.83 | 0.83 | 0.83 |
| Five clusters | 1.27 | 1.21 | 1.17 | 1.14 | 1.12 | 1.08 | 1.05 | 1.03 | 0.98 |
| Bisymmetrical clusters |
1.37 | 1.30 | 1.28 | 1.27 | 1.20 | 1.19 | 1.06 | 1.04 | 1.03 |
| Sixteen points per regular cluster |
1.49 | 1.39 | 1.37 | 1.36 | 1.35 | 1.32 | 1.27 | 1.24 | 1.13 |
| One cluster | 2.26 | 2.25 | 2.24 | 2.23 | 2.22 | 2.22 | 2.20 | 2.20 | 2.19 |
Table B.5--Average standard error first-degree polynomial drift unit density and unit linear semivariogram slope
| Pattern | Number of nearest neighbors | |||||||
|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 8 | 12 | 16 | 32 | |
| Hexagonal | 0.65 | 0.64 | 0.63 | 0.63 | 0.63 | 0.63 | 0.63 | 0.63 |
| Square | 0.66 | 0.65 | 0.64 | 0.64 | 0.64 | 0.64 | 0.64 | 0.64 |
| Triangular | 0.80 | 0.69 | 0.67 | 0.67 | 0.66 | 0.66 | 0.66 | 0.66 |
| Orthogonal traverses every 2 points |
1.02 | 0.77 | 0.72 | 0.70 | 0.69 | 0.69 | 0.68 | 0.68 |
| Hexagonal stratification |
1.47 | 0.74 | 0.70 | 0.69 | 0.69 | 0.69 | 0.69 | 0.69 |
| Square stratification |
1.81 | 0.75 | 0.71 | 0.70 | 0.69 | 0.69 | 0.69 | 0.69 |
| Random | 1.91 | 0.96 | 0.82 | 0.77 | 0.73 | 0.72 | 0.71 | 0.71 |
| Bisymmetrical random |
21.92 | 0.84 | 0.77 | 0.74 | 0.72 | 0.72 | 0.72 | 0.72 |
| Orthogonal traverses every 8 points |
1.24 | 1.14 | 1.02 | 0.88 | 0.83 | 0.81 | ||
| Four points per regular cluster |
1.99 | 1.56 | 1.09 | 1.01 | 0.92 | 0.83 | 0.83 | 0.83 |
| Five clusters | 3.69 | 2.71 | 2.20 | 1.98 | 1.60 | 1.33 | 1.18 | 0.99 |
| Bisymmetrical clusters |
2.50 | 2.24 | 1.93 | 1.18 | 1.07 | 1.03 | ||
| Sixteen points per regular cluster |
2.96 | 2.75 | 2.29 | 1.83 | 1.62 | 1.17 | ||
| One cluster | 148.00 | 33.87 | 19.74 | 13.92 | 9.17 | 7.15 | 6.31 | 5.01 |
Table B.6--Average standard error second-degree polynomial drift unit density and unit linear semivariogram slope
| Pattern | Number of nearest neighbors | ||||||
|---|---|---|---|---|---|---|---|
| 6 | 7 | 8 | 9 | 12 | 16 | 32 | |
| Hexagonal | 0.68 | 0.67 | 0.66 | 0.65 | 0.63 | 0.63 | 0.63 |
| Square | 0.67 | 0.67 | 0.66 | 0.64 | 0.64 | 0.64 | |
| Triangular | 0.77 | 0.72 | 0.69 | 0.66 | 0.66 | 0.66 | |
| Orthogonal traverses every 2 points |
0.76 | 0.71 | 0.69 | 0.68 | |||
| Hexagonal stratification |
1.55 | 0.86 | 0.77 | 0.74 | 0.70 | 0.69 | 0.69 |
| Square stratification |
3.27 | 0.90 | 0.78 | 0.74 | 0.71 | 0.70 | 0.69 |
| Random | 26.71 | 1.42 | 1.06 | 0.88 | 0.77 | 0.74 | 0.71 |
| Bisymmetrical random |
0.85 | 0.76 | 0.73 | 0.72 | |||
| Orthogonal traverses every 8 points |
1.69 | 1.30 | 1.16 | 0.84 | |||
| Four points per regular cluster |
1.11 | 1.02 | 0.95 | 0.84 | |||
| Five clusters | 88.99 | 17.76 | 12.80 | 9.68 | 4.90 | 2.71 | 1.07 |
| Bisymmetrical clusters |
9.92 | 1.62 | 1.11 | ||||
| Sixteen points per regular cluster |
12.94 | 7.25 | 4.78 | 1.53 | |||
| One cluster | 2214.00 | 936.00 | 547.00 | 275.00 | 171.00 | 61.50 | |
Table B.7--Maximum standard error the drift is a constant unit density and unit linear semivariogram slope
| Pattern | Number of nearest neighbors | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 6 | 8 | 12 | 16 | 32 | |
| Hexagonal | 1.11 | 0.84 | 0.72 | 0.72 | 0.72 | 0.72 | 0.72 | 0.72 | 0.72 |
| Square | 1.19 | 0.88 | 0.80 | 0.75 | 0.75 | 0.75 | 0.74 | 0.74 | 0.74 |
| Triangular | 1.32 | 1.14 | 0.98 | 0.88 | 0.81 | 0.81 | 0.80 | 0.80 | 0.80 |
| Orthogonal traverses every 2 points |
1.50 | 1.27 | 1.14 | 1.05 | 0.93 | 0.91 | 0.90 | 0.89 | 0.89 |
| Hexagonal stratification |
1.30 | 1.07 | 1.02 | 0.94 | 0.87 | 0.86 | 0.86 | 0.86 | 0.86 |
| Square stratification |
1.42 | 1.26 | 1.06 | 0.97 | 0.93 | 0.92 | 0.91 | 0.91 | 0.91 |
| Random | 1.48 | 1.34 | 1.34 | 1.23 | 1.16 | 1.06 | 1.06 | 1.05 | 1.05 |
| Bisymmetrical random |
1.60 | 1.45 | 1.33 | 1.32 | 1.05 | 1.00 | 0.99 | 0.99 | 0.98 |
| Orthogonal traverses every 8 points |
2.01 | 1.94 | 1.80 | 1.76 | 1.31 | 1.39 | 1.29 | 1.24 | 1.23 |
| Four points per regular cluster |
1.60 | 1.50 | 1.41 | 1.40 | 1.17 | 1.12 | 1.00 | 1.00 | 0.99 |
| Five clusters | 1.83 | 1.82 | 1.75 | 1.74 | 1.70 | 1.67 | 1.64 | 1.46 | 1.33 |
| Bisymmetrical clusters |
1.92 | 1.83 | 1.83 | 1.83 | 1.76 | 1.76 | 1.40 | 1.39 | 1.22 |
| Sixteen points per regular cluster |
2.19 | 2.06 | 2.06 | 2.05 | 2.05 | 1.90 | 1.90 | 1.74 | 1.51 |
| One cluster | 2.99 | 2.98 | 2.98 | 2.98 | 2.97 | 2.96 | 2.96 | 2.95 | 2.94 |
Table B.8--Maximum standard error first-degree polynomial drift unit density and unit linear semivariogram slope
| Pattern | Number of nearest neighbors | |||||||
|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 8 | 12 | 16 | 32 | |
| Hexagonal | 0.73 | 0.73 | 0.72 | 0.72 | 0.72 | 0.72 | 0.72 | 0.72 |
| Square | 0.84 | 0.75 | 0.75 | 0.75 | 0.75 | 0.74 | 0.74 | 0.74 |
| Triangular | 1.47 | 0.93 | 0.83 | 0.81 | 0.81 | 0.80 | 0.80 | 0.80 |
| Orthogonal traverses every 2 points |
2.45 | 1.40 | 1.02 | 0.94 | 0.91 | 0.90 | 0.89 | 0.89 |
| Hexagonal stratification |
15.39 | 1.30 | 0.89 | 0.87 | 0.86 | 0.86 | 0.86 | 0.86 |
| Square stratification |
23.01 | 1.75 | 0.99 | 0.93 | 0.92 | 0.91 | 0.91 | 0.91 |
| Random | 19.74 | 3.26 | 1.84 | 1.58 | 1.11 | 1.06 | 1.05 | 1.05 |
| Bisymmetrical random |
307.00 | 3.02 | 1.36 | 1.14 | 1.00 | 0.99 | 0.99 | 0.98 |
| Orthogonal traverses every 8 points |
2.58 | 2.21 | 1.77 | 1.45 | 1.25 | 1.23 | ||
| Four points per regular cluster |
3.94 | 2.38 | 2.11 | 1.87 | 1.54 | 1.00 | 1.00 | 0.99 |
| Five clusters | 12.35 | 11.76 | 5.33 | 5.23 | 4.24 | 3.26 | 2.28 | 1.49 |
| Bisymmetrical clusters |
6.04 | 5.12 | 4.22 | 2.26 | 1.98 | 1.22 | ||
| Sixteen points per regular cluster |
5.80 | 5.48 | 4.17 | 3.72 | 2.90 | 1.85 | ||
| One cluster | 793.00 | 118.00 | 98.19 | 46.45 | 18.47 | 12-55 | 10.13 | 8.27 |
Table B.9--Maximum standard error second-degree polynomial drift unit density and unit linear semivariogram slope
| Pattern | Number of nearest neighbors | ||||||
|---|---|---|---|---|---|---|---|
| 6 | 7 | 8 | 9 | 12 | 16 | 32 | |
| Hexagonal | 0.78 | 0.76 | 0.76 | 0.74 | 0.72 | 0.72 | 0.72 |
| Square | 0.79 | 0.78 | 0.77 | 0.75 | 0.74 | 0.74 | |
| Triangular | 1.07 | 0.99 | 0.87 | 0.80 | 0.80 | 0.80 | |
| Orthogonal traverses every 2 points |
1.27 | 0.97 | 0.90 | 0.89 | |||
| Hexagonal stratification |
39.91 | 1.57 | 1.14 | 1.07 | 0.90 | 0.87 | 0.86 |
| Square stratification |
93.17 | 3.07 | 1.42 | 1.12 | 0.96 | 0.93 | 0.91 |
| Random | 2690.00 | 11.60 | 7.90 | 2.03 | 1.32 | 1.15 | 1.05 |
| Bisymmetrical random |
1.96 | 1.25 | 1.07 | 0.98 | |||
| Orthogonal traverses every 8 points |
8.84 | 4.48 | 3.27 | 1.45 | |||
| Four points per regular cluster |
1.67 | 1.43 | 1.22 | 1.00 | |||
| Five clusters | 986-00 | 142.00 | 101.00 | 101.00 | 32.87 | 12.30 | 2.33 |
| Bisymmetrical clusters |
107.00 | 10.03 | 1.38 | ||||
| Sixteen points per regular cluster |
33.47 | 23.71 | 12.10 | 5.13 | |||
| One cluster | 10425.00 | 8763.00 | 1956.00 | 815.00 | 535.00 | 148.00 | |
Find the best non-regular sampling procedure for the High Plains aquifer which will produce estimates of the water table elevation having an average standard error of 10.8 feet (3.3 m). Border effects will be ignored.
From Algorithm 2.1
1. The results of the structural analysis are given in Appendix A. The relevant results are:
a. ω = 60 feet2 per mile (3.5 m2/km)
b. The drift model is a first degree polynomial within a neighborhood which is 28 miles (45 km) in diameter.
2. From the statement of the problem, the sampling efficiency index is the average standard error.
3. From Table B.1, the non-regular patterns with lowest average standard error are the stratified patterns. A hexagonal stratification is preferred over a square stratification as the former offers a lower maximum standard error. The value I(1,1)is 0.69 feet (0.21 m).
4. From the statement of the problem, I(ω,ρ)is equal to 10.8 feet (3.3 m).
5. From equation 2.4 and the steps above
ρ = 602 [0.69 / 10.8]4
= 0.06 point per square mile
6. The number of points inside a 28 mile (45 km) diameter at a density of 0.06 point per square mile (0.023 point/km2) is
N = (πd2 / 4) ρ
= (3.14159 × 282 × 0.06) / 4
= 36 points
7. From Table B.3, the minimum number of nearest neighbors required to solve the universal kriging system of equations is 3, which is an order of magnitude smaller than the number of points that can be contained inside the neighborhood for which structural analysis models are valid.
8. From Table B.2, the point of no return is 6.
9. Since the 36 points that can be placed inside the structural analysis neighborhood is a larger number than the point of no return, 6 nearest neighbors should be used in the solution of the universal kriging system of equations.
Hence, the best irregular sample pattern for the water table elevation in the High Plains aquifer is a hexagonal stratified pattern. Except near the edges of the aquifer, a sampling density of 0.06 point per square mile (0.023 point/km2)assures an average standard error of 10.8 feet (3.3 m). The number of sample elements to be used in the universal kriging system of equations should be 6.
The distance index is a measure of randomness in a two-dimensional process. Let us consider a sample of n points. Each point will have a nearest neighbor which is some distance ri away. The average distance to the nearest neighbor, ![]() is defined as
is defined as
![]() = (1/n) ∑ni=1 ri (D.1)
= (1/n) ∑ni=1 ri (D.1)
Clark and Evans (1954)proved that the expected average distance to the nearest neighbor in a random pattern is
![]() E = 1 / 2√ρ (D.2)
E = 1 / 2√ρ (D.2)
where ρ is the density of the pattern expressed as the number of sample elements per unit of area.
The distance index R is the ratio of the observed average distance to the nearest neighbor to the value expected for a random pattern:
R = ![]() /
/ ![]() E (D.3)
E (D.3)
The distance index R can vary between zero, for a cluster in which all sample elements occur at the same location, to a maximum value of 2.149, for a regular hexagonal pattern such as Figure B.1a.
Prev Page--Start of Report || Next Page--Data Listings
Kansas Geological Survey, High Plains Aquifer Observation Network
Placed on web June 25, 2012; originally published in 1982.
Comments to webadmin@kgs.ku.edu
The URL for this page is http://www.kgs.ku.edu/Publications/Bulletins/GW7/02_append.html