Prev Page--Hydrologic setting || Next Page--Water quality
Digital Model of Wellington Aquifer
A two-dimensional finite-difference steady-state digital ground-water flow model developed by Trescott, Pinder, and Larson (1976) was used as an aid in understanding the hydraulic characteristics of the Wellington aquifer and in determining if the observed, or conceptual, potentiometric map was mathematically feasible. The modeled area, which exceeds 1,500 mi2, was subdivided into a variably spaced rectangular finite-difference grid of 22 rows and 69 columns (pl. 4).
It is believed that the Wellington aquifer system does not have horizontal outflow. Instead, discharges are vertically upward from the saltwater aquifer into overlying freshwater deposits. (The method of determining the rate of natural discharge from the Wellington aquifer is described later in the "Water Quality" section.) Because the model was intended to be a simplified method of simulating the observed discharge and potentiometric surface, constant head nodes were placed at the upgradient end of the areas where discharge occurs (pl. 4). The altitudes assigned to the constant head nodes were derived from the observed potentiometric map.
Aquifer Properties
Occurrence of ground water in the Wellington aquifer evidently is the result of leakage from overlying unconsolidated deposits through the upper Wellington member. Because the member is a relatively impermeable confining bed, leakage must be through fractures and slumping that resulted from dissolution of salt and collapse of overlying beds. Thus, the vertical-leakage rate through the confining bed is calculated at each node in the model by solution of the equation
q = (k/m) (h1 - h0)
where
q = leakage per unit area through the confining bed, in feet per second;
k = hydraulic conductivity of the confining bed, in feet per second;
m = thickness of the confining bed, in feet;
h1 = head at the top of the confining bed, in feet; and
h0 = head in the Wellington aquifer at the start of the simulation period, in feet.
The rate of vertical leakage through the confining bed was calculated by the digital model to equal 0.7 ft3/s, as explained in the section, "Results of Digital Model Simulation."
The Home Petroleum Company at Conway reports that during the summer of 1968 through the winter of 1974-75, 25,878,201 bbl of saltwater were removed from the Wellington aquifer and 27,052,278 bbl were injected. This was a net increase for the period of 1,174,077 bbl or an average of 460 bbl per day (0.03 ft3/s). Also the Kansas Department of Health and Environment reports that, as of 1975, there were 30 wells through which disposal of saltwater to the Wellington aquifer was allowed. The total allocated disposal rate was 9,336 bbl per day (0.61 ft3/s). This equals a maximum of 0.64 ft3/s of saltwater disposal through all wells into the system. The wells were represented by 18 nodes in the model. The amount of disposal allocated per node was based on the number of wells and disposal rate per node. About 90 percent of the disposal occurs between Salina and McPherson.
Data indicating the transmissivity of the Wellington aquifer in the vicinity of Conway is available from one aquifer test performed by the U.S. Geological Survey at the Home Petroleum Company in Hay 1977. The average transmissivity derived from this test was 0.0289 ft3/s. The Wellington aquifer in this local area may be very cavernous and well developed owing to the cyclical pumpage and injection of saline water in conjunction with the aforementioned LPG operations. Thus, the transmissivity value may be relatively large when compared with the remainder of the aquifer system. Transmissivity values were adjusted in other areas as discussed later.
Calibration of Model
To ascertain whether the digital model of the Wellington aquifer is a viable simulation, water-level measurements from the field should be compared with corresponding output from the model.
It was assumed that the potentiometric surface defined by water-level measurements represents a steady-state flow system. The model then computes a potentiometric surface based upon the input data on aquifer properties, boundaries, and hydraulic stresses.
One objective of the calibration procedure is to minimize differences between the observed and computed potentiometric surfaces by manipulating input data (aquifer properties, boundary conditions, and hydraulic stresses). Obviously, many interrelated factors affect ground-water flow; thus, the manipulation of this data is highly subjective. The degree of adjustment of any parameter is relative to the uncertainty of its value; i.e., the disposal rates into the Wellington aquifer (0.64 ft3/s) and natural discharge from the aquifer (1.36 ft3/s) are reasonably determined, and thus were not adjusted. (The method of determining the rate of natural discharge is discussed later in the "Water Quality" section.) However, the values for aquifer transmissivity and hydraulic conductivity of the confining bed are poorly known, and various values were assumed during the calibration of the model. All changes in parameters were made uniformly over an area, rather than on a node-to-node basis, to arrive at an acceptable match between calculated and observed heads.
Development of the final model simulation was an evolutionary process in which adjustments to the model were based on results of previous simulations. Initially, a uniform transmissivity and zero hydraulic conductivity (zero leakage) of the confining bed were assumed. Use of these criteria, however, showed little agreement between the calculated head distribution and discharge rate from the system and those from observed conditions.
Several simulations were made using values of hydraulic conductivity for typically Impermeable shale (1.0 x 10-10 to 1.0 x 10-12 ft/s) in conjunction with transmissivity values that ranged from 0.0116 ft2/s to O.0578 ft2/s (approximately one-half and two times the transmissivity value derived from the aquifer test). These values were applied uniformly over the modeled area or variably over major areas. It was found that a value of 3 x 10-11 ft/s for hydraulic conductivity of the confining layer and values of transmissivity of about 0.03 ft2/s in the northern half of the study area and 0.01 ft2/s in the southern half generally gave results in which calculated and observed values of head distribution and discharge were relatively agreeable (pl. 4).
One notable exception to the general agreement occurs in the three-township area east of Hutchinson. The calculated head distribution was on the order of 80 to 100 feet below the observed head distribution. It is evident from the very steep ground-water gradients and the lack of similarity between calculated and observed aquifer characteristics that some anomalous conditions occur within this area.
There is no evidence of faulting in the shallow subsurface in this area that could cause a discontinuity of the ground-water flow pattern. It is possible that the two areas of steep hydraulic gradient may represent zones of exceedingly low hydraulic conductivity in the aquifer, which may be the result of minor dissolution, poor interconnection of solution cavities, and little settling and compaction of thick overlying shales. This also maybe true in other) areas but may not be evident owing to the sparse control and consequent lack of definition of the observed potentiometric surface.
Assuming that poor hydraulic connection did exist across the zones of steep gradient, these zones were assigned very low values of transmissivity ranging from 0.0001 ft2/s to 0.0022 ft2/s (pl. 4). Using this approach, a reasonable match was generated between the observed and calculated potentiometric surfaces (pl. 4) and the observed and calculated discharge (1.36 ft3/s and 1.46 ft3/s, respectively).
Another objective of calibrating the digital model is to determine the sensitivity of the model to various combinations of aquifer parameters. By using sensitivity analysis, it is possible to judge which factors most affect ground-water flow in the aquifer system.
Figure 8 shows results of the sensitivity analysis that was performed on the digital model of the Wellington aquifer. A "best fit" was attained between the observed and calculated head distributions as previously discussed. Then values of transmissivity were Increased and decreased 50 percent to ascertain the effect on: (1) the absolute value of the sums of the drawdown residuals and (2) the calculated discharge from the system. The absolute value of the sums of the drawdown residuals was determined by summing the differences between the observed head and the head calculated by the digital model at each node. Figure 8A shows that, as transmissivity in the system was lowered by 50 percent, the absolute value of the sums of the drawdown residuals increased from 4,535 to 16,310. and discharge decreased from 1.46 ft3/s to 1.15 ft3/s. Conversely, as transmissivity was increased by 50 percent, the absolute value of the sums of the head residuals increased from 4,535 to 12,485, and discharge increased from 1.46 ft3/s to 1.85 ft3/s.
Figure 8. Relation between (A) percentage changes in transmissivity and (B) hydraulic conductivity versus the absolute value of the sum of the drawdown residuals and discharge from the Wellington aquifer.
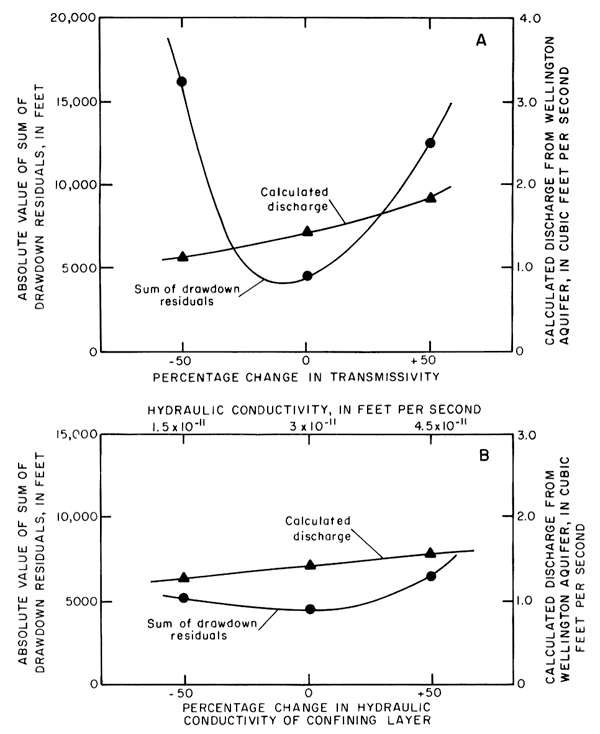
Figure 8B shows the results of the sensitivity analysis when transmissivity was held constant and the hydraulic conductivity of the confining bed was changed by 50 percent. As the hydraulic conductivity was increased from 3 x 10-11 ft/s to 4.5 x 10-11 ft/s, the absolute value of the sum of the drawdown residuals increased from 4,535 to 6,517, and discharge increased from 1.46 ft3/s to 1.57 ft3/s. Conversely, when hydraulic conductivity of the confining bed was decreased to 1.5 X 10-11 ft/s, the absolute value of the sum of the drawdown residuals increased from 4,535 to 5,033, and the discharge decreased from 1.46 ft3/s to 1.31 ft3/s.
Figure 8 shows that changes in transmissivity over a range of 100 percent have more effect on discharge than corresponding changes in hydraulic conductivity of the confining bed. Thus, the model is more sensitive to changes in transmissivity than to changes in hydraulic conductivity of the confining bed.
Also, the effect on the absolute value of the sum of the drawdown residuals of positive or negative changes in transmissivity over a range of 100 percent is greater than the effect of such changes in hydraulic conductivity. Conversely, when considering the effects of changes in hydraulic conductivity on the absolute value of the sum of the drawdown residuals, figure 8B shows that an increase of 50 percent in hydraulic conductivity of the confining bed causes a larger increase in the absolute value of the sum of the drawdown residuals than a 50 percent decrease in the hydraulic conductivity of the confining bed.
Results of Digital Model Simulation
The steady-state potentiometric surface of the Wellington aquifer calculated by the calibrated digital model is shown on plate 4. The major features of the observed potentiometric surface generally are well matched by results from the digital model. The calculated surface shows: (1) the relatively high potentiometric surface in the area just east of Hutchinson, which is bounded on the northeast and southeast by two zones of steep hydraulic gradient, and (2) gradual hydraulic gradients north and southeast of these zones toward out-flow areas in the Smoky Hill River valley and in the Belle Plaine-Adamsville-Geuda Springs area, respectively.
The observed and calculated head distributions do not agree along the western edge of the Wellington aquifer in the area west of Belle Plaine. In this area, the calculated heads are lower than the observed heads. A constant value for hydraulic conductivity was assigned to each node in the model. Perhaps an increase in the leakage rate through the confining layer in this area would allow a better match between the observed and calculated potentiometric surfaces. Alternatively, the transmissivity values used in this part of the digital model may be greater than in the physical system. Decreasing the values of transmissivity would tend to elevate the calculated heads.
During the calibration process, a mass balance for each simulation was computed to check the numerical accuracy of the solution. Incorporated in the mass balance is the net flux contributed by each hydrologic component of the model. These fluxes are tabulated as part of the hydrologic budget. The hydrologic budget for the calibrated steady-state simulation run consists of: (1) injection of saline water into the Wellington aquifer via wells, (2) recharge of fresh water to the Wellington aquifer via leakage from the freshwater-bearing deposits through the overlying confining bed, and (3) discharge of saline water from the Wellington aquifer to the various freshwater systems. This hydrologic budget can be written in the form:
RW + R1 = -Q,
where
RW = recharge via wells;
R1 = recharge via areal leakage; and
Q = discharge from the Wellington aquifer.
Observed discharge from the Wellington aquifer is estimated to be 1.36 ft3/s, and the discharge calculated by the digital model is 1.46 ft3/s. Recharge to the aquifer via wells is estimated to be 0.64 ft3/s. Using the hydrologic budget outline above, recharge to the aquifer via areal leakage through the confining bed should be about 0.7 ft3/s. The areal leakage calculated by the digital model was 0.6 ft3/s, indicating a reasonably good match.
The reasonable match between observed and calculated heads, between observed and calculated discharges, and between the areal leakage derived from the hydrologic budget and the calculated areal leakage indicates that the conceptual model is numerically possible and hydrologically valid.
Prev Page--Hydrologic setting || Next Page--Water quality
Kansas Geological Survey, Geology
Placed on web Jan. 2006; originally published 1981.
Comments to webadmin@kgs.ku.edu
The URL for this page is http://www.kgs.ku.edu/Publications/Bulletins/CQS9/05_digit.html