


Kansas Geological Survey, Current Research in Earth Sciences, Bulletin 247,
part 1
Modeling Dielectric-constant Values of Geologic Materials: An Aid to Ground-penetrating Radar Data Collection and Interpretation--page 4 of 13

Dielectric Constant and Ground-penetrating Radar
The results of dielectric-constant modeling can be used in planning GPR data acquisition and in interpreting GPR data. For data acquisition, modeling results can be used to determine whether a feature or interface will result in measurable reflections, and if so, the expected two-way reflection travel-times (TWT) and antenna frequencies needed for imaging. For interpretation, dielectric-modeling results can be used to better understand recorded travel-times and amplitude variations, the controlling factors on measured dielectric property values. These results are also necessary for inverse modeling sediment or rock properties from GPR response. A review of the equations governing GPR response illustrates the role of dielectric constant.
All equations presented below assume that reflections are at or near vertical incidence and that the material through which the EM waves travel is of low conductivity (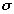 ‹ 10 mS/m) and nonmagnetic (
‹ 10 mS/m) and nonmagnetic (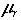 = 1). (When reflections are not at vertical incidence, the more general relationships presented in Baker, 1998, and Reppert et al., 1999, become more valid mathematical representations of the electromagnetic wave-field response.) The assumptions of low-conductivity and nonmagnetic material are valid for most nonclayey, sedimentary materials containing freshwater in their pore spaces. The results of the equations become less valid as conditions vary from the initial assumptions (i.e.,
= 1). (When reflections are not at vertical incidence, the more general relationships presented in Baker, 1998, and Reppert et al., 1999, become more valid mathematical representations of the electromagnetic wave-field response.) The assumptions of low-conductivity and nonmagnetic material are valid for most nonclayey, sedimentary materials containing freshwater in their pore spaces. The results of the equations become less valid as conditions vary from the initial assumptions (i.e., 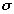 › 10 mS/m and
› 10 mS/m and 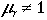 ) due to the dispersive effect of conductivity and the added influence of relative magnetic permeability on wave propagation.
) due to the dispersive effect of conductivity and the added influence of relative magnetic permeability on wave propagation.
Reflection Coefficients and Power Reflectivity
The reflection coefficient (RC) of GPR signals in nonmagnetic material is a function of electromagnetic impendance (EM). If EM is replaced with its equivalent, the square root of the dielectric constant, the reflection coefficient can be calculated:
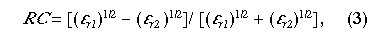
where 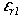 is the dielectric constant of the upper media and
is the dielectric constant of the upper media and 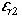 is the dielectric constant of the lower media. Equation (3) can be used to determine the strength of reflections at interfaces of materials of different lithology or water saturations (i.e., different bulk dielectric constants). Worksheet 4 (appendix A) can be used to calculate the change in reflection coefficient as the result of dielectric-constant change between materials.
is the dielectric constant of the lower media. Equation (3) can be used to determine the strength of reflections at interfaces of materials of different lithology or water saturations (i.e., different bulk dielectric constants). Worksheet 4 (appendix A) can be used to calculate the change in reflection coefficient as the result of dielectric-constant change between materials.
Power reflectivity (Pr) is a measure of the energy reflected by a target back to a receiving antenna. If the power reflectivity is too low compared to background clutter (noise), then a reflection may not be recorded by a GPR system—in other words, the signal-to-noise ratio (SNR) is below 1. The power reflectivity (Pr) of an interface may be estimated using the relationship presented by Annan (1996):

A conservative guideline is that power reflectivity should be greater than 0.01 or that RC should exceed 0.10 (Annan, 1996) in order for GPR to discern a reflection above background noise for single-fold data. The power reflectivity is greater in low-loss, low-EM noise regions and can be increased in high-noise regions using vertical and CMP stacking (the summing of traces). The power reflectivity decreases for targets with diameters less than the EM wavelength or in regions with high loss and high EM noise. Annan’s (1996) reflection-coefficient threshold of 0.10 is only a general guideline, but it provides a useful frame of reference. The SNR of a reflection increases as a function of the square root of the number of stacks (Yilmaz and Doherty, 1987); therefore, stacking may allow low power reflectivity reflections to be recorded (fig. 3). Unlike seismic data, where stacking requires considerably greater effort, obtaining 64 or 128 vertical stacks of a GPR trace may only take several seconds longer than a single-fold trace.
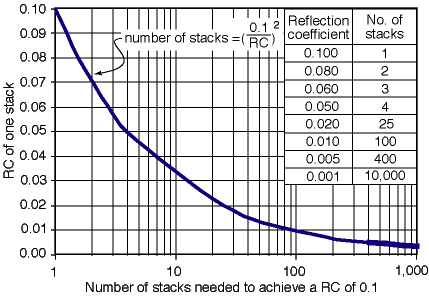
Fig. 3. Plot of the reflection coefficient of single-fold data versus the number of stacks needed to achieve a reflection coefficient of 0.1, the minimum threshold value established by Annan (1996),in which the signal-to-noise (SNR) ratio is approximately 1. The values are calculated using the assumption that stacking increases the SNR by a factor of the square root of the number of stacks, which is true for random noise (Yilmaz and Doherty, 1987).
Velocity and Travel-time
The velocity (V) at which electromagnetic waves travel through low-loss materials is described by the relationship:

where c is the speed of light in a vacuum (3 X 108 m/s). Because dielectric-constant values of rock exceed the dielectric constant of a vacuum (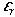 = 1), electromagnetic velocity is greatest in a vacuum and decreases with increasing dielectric constant. Velocity information can be used to calculate expected two-way travel-times (TWT) of reflections using the relationship:
= 1), electromagnetic velocity is greatest in a vacuum and decreases with increasing dielectric constant. Velocity information can be used to calculate expected two-way travel-times (TWT) of reflections using the relationship:

where d is distance to the reflector. Travel-times determine the optimal data recording time-window for a GPR survey and are essential to the interpretation of GPR data. Travel-times provide expected reflection times for reflectors at given depths and predict the maximum depth of meaningful GPR penetration.
Kansas Geological Survey
Web version December 3, 2001
http://www.kgs.ku.edu/Current/2001/martinez/martinez4.html
email:lbrosius@kgs.ku.edu
![]()

