The dielectric mixing model found by the authors to be the most useful and easiest to implement for geologic materials is the Time-Propagation (TP) model, a volumetric model. Not only are the input parameters easily obtained, but the mathematical equation to calculate bulk dielectric-constant values is simple (and therefore widely usable) and the results of the TP model are very similar to observed values. The mathematical equation describing the TP dielectric mixing model is:
![]()
where Vi and ![]() are the bulk volume fraction and dielectric constant, respectively, of the ith component (Knoll, 1996). Equation (1) is a specific instance of the more general Lichtenecker-Rother equation (Lichtenecker and Rother, 1931):
are the bulk volume fraction and dielectric constant, respectively, of the ith component (Knoll, 1996). Equation (1) is a specific instance of the more general Lichtenecker-Rother equation (Lichtenecker and Rother, 1931):
![]()
where ![]() a geometric factor that relates the direction of the effective layering of components to the direction of the applied electrical field, is 0.5 (Knoll, 1996). The TP model does not account for variations in frequency; therefore, modeled bulk dielectric-constant values are valid only at the specific frequency for which the input component dielectric constants are representative. This model also does not account for the effects of dielectric loss or magnetic permeability; therefore, it is valid only for predicting the dielectric constant of low-loss (i.e., low conductivity;
a geometric factor that relates the direction of the effective layering of components to the direction of the applied electrical field, is 0.5 (Knoll, 1996). The TP model does not account for variations in frequency; therefore, modeled bulk dielectric-constant values are valid only at the specific frequency for which the input component dielectric constants are representative. This model also does not account for the effects of dielectric loss or magnetic permeability; therefore, it is valid only for predicting the dielectric constant of low-loss (i.e., low conductivity; ![]() ‹ 10 mS/m), nonmagnetic (i.e.,
‹ 10 mS/m), nonmagnetic (i.e., ![]() 1) materials.
1) materials.
Because at a given frequency there are three principal variables (mineralogy, porosity, and water saturation) exerting control on bulk dielectric-constant values in low-loss rocks and soils, it is possible to represent the TP model results in four-dimensions (termed TP-model dielectric-constant space on fig. 1). For most rocks and soils, porosity ranges from 0% to 50% (expressed as percent of total rock volume) and water saturation ranges from 0% to 100% (expressed as percentage of pore volume). It is convenient to express mineralogy in units of the dielectric constant of the mineral mixture at zero porosity and water saturation. On this basis, the influence of mineralogy for most common rocks and soils ranges from a low value exhibited by quartz (Xm ![]() 4) to a high value exhibited by kaolinite (Xm
4) to a high value exhibited by kaolinite (Xm ![]() 12).
12).
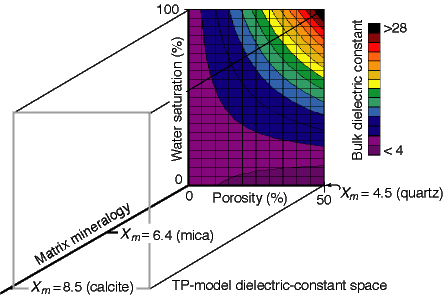
Fig. 1. Four-dimensional representation (termed TP-model dielectric-constant space) of the TP-model input parameters (matrix mineralogy, porosity, and water saturation) and resulting bulk dielectric constant values (shown in color). The matrix mineralogy axis (Xm) is the dielectric-constant value of the matrix components at zero porosity and water saturation. The locations of quartz, mica, and calcite are indicated on the Xm axis. For most earth materials, porosity ranges from 0% to 50%, and water saturation ranges from 0% to 100%. Calculated bulk dielectric-constant values range from greater than 4 to less than 28. The N-Sw planes through Xm = 4.5 (quartz) and Xm = 8.5 (calcite) are shown in fig. 2.
Many GPR investigations are conducted in the vadose zone where water saturations can vary with the capillary-pressure properties of the rock or soil. Figure 2A shows the relationship between bulk dielectric constant and both porosity and water saturation for a quartz matrix (Xm = 4.5). At water saturations below approximately 20%, which can be common in the vadose zone for many higher porosity rocks and soils, bulk dielectric constant remains below 6.0 for porosities ranging from zero to 50%. Even for rocks with minerals exhibiting relatively high dielectric-constant values (e.g., calcite, ![]() = 8.5), the bulk dielectric constant is less than 8.0 (fig. 2B). These low bulk dielectric-constant values are mainly the result of the low dielectric constant of the minerals and the low dielectric constant of air (
= 8.5), the bulk dielectric constant is less than 8.0 (fig. 2B). These low bulk dielectric-constant values are mainly the result of the low dielectric constant of the minerals and the low dielectric constant of air (![]() = 1.0) occupying the pore space. As water saturation increases, the higher dielectric constant of water (
= 1.0) occupying the pore space. As water saturation increases, the higher dielectric constant of water (![]() = 81) increases bulk dielectric-constant values to greater than 30 (fig. 2). Worksheets 2 and 3 (appendix A) allow construction of figures similar to fig. 2 for user-defined porosity, mineralogy, and water saturation.
= 81) increases bulk dielectric-constant values to greater than 30 (fig. 2). Worksheets 2 and 3 (appendix A) allow construction of figures similar to fig. 2 for user-defined porosity, mineralogy, and water saturation.
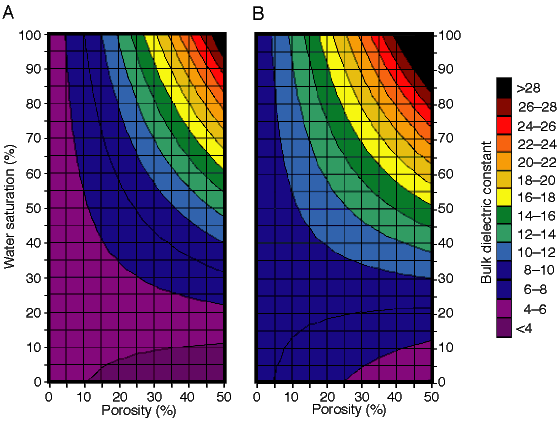
Fig. 2. TP-modeled bulk dielectric constants for (A) Xm = 4.5 (quartz) and (B) Xm = 8.5 (calcite), with porosities ranging from 0% to 50% and water saturations ranging from 0% to 100%. At low water saturations, bulk dielectric constant values decrease slowly with increasing porosity due to the increased influence of air (![]() = 1), which has a dielectric constant near that of common earth materials (
= 1), which has a dielectric constant near that of common earth materials (![]()
![]() 4-12). At high water saturations, bulk dielectric constant values increase rapidly with increasing porosity due to the increased influence of the high dielectric constant of water (
4-12). At high water saturations, bulk dielectric constant values increase rapidly with increasing porosity due to the increased influence of the high dielectric constant of water (![]() = 81).
= 81).
Kansas Geological Survey
Web version December 3, 2001
http://www.kgs.ku.edu/Current/2001/martinez/martinez3.html
email:lbrosius@kgs.ku.edu