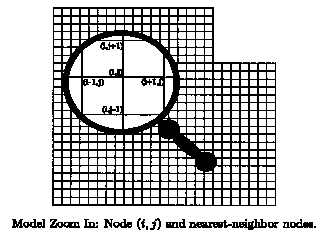
To accomplish this we must first choose an empty lattice node that has at least one adjacent node that is filled. What is meant by adjacent is shown below; the node (i, j) has four adjacent nodes: (i+1, j), (i, j+1), (i -1, j), and (i, j-1).

We find a qualified node by randomly picking a lattice node (i, j). If it is filled, or if it does not have any adjacent nodes that are filled, we choose another (as in the initialization phase, this process of finding a qualified node takes very little time, on average). We need an empty node with at least one adjacent node filled in order for there to be the potential for growth to (i, j). Once we have a qualified lattice node (i, j), there are two possibilities for filling that node: An element may grow from one of the adjacent nodes, or a new element may be introduced. This mimics what we observe in the field; elements may extend across several nodes and then stop.
We consider any element in a filled node that is adjacent to (i, j) to have the potential to grow into (i, j). Also, any element that is not in an adjacent node has the potential to be introduced as an element in (i, j). These potentials are computed as probabilities: A growth probability qk for each element k that is in an adjacent node, and an introduction probability rk for each element k that is not. The growth probabilities qk are calculated using the geological properties of the element (e.g. current size and shape as compared to field observations, paleocurrent trends). The introduction probabilities rk are calculated using the frequency of occurrence and known geological behavior (for instance, channels are less likely to suddenly appear and disappear, but more likely to grow from border to border of the region).
An example will help illustrate our method: Consider the empty lattice node (i, j) as shown below, surrounded by empty nodes (i+1, j) and (i, j+1), and filled nodes (i-1,j) (filled with element a) and (i, j-1) (filled with element b).
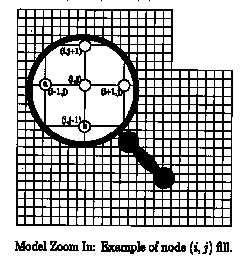
Based on the current properties of element a in the model, we calculate a probability qa that it will grow into node (i, j). Likewise, we calculate a probability qb that element b will grow into node (i, j). Assuming that there are n elements possible in this model, number the remaining elements (other than elements a and b) from 1 to n-2. For each element k that is not in an adjacent node, we calculate a probability rk that element k will be introduced at the node (i, j). These probabilities are closely tied to the observation frequency of the elements, while considering the behavior of the elements and how likely they are to suddenly appear at a unique position on the model.
Previous Page--Initialization ||
Next Page--More on model generation
Dakota Home ||
Start of the Stochastic Modeling Report