|
|
|
Background Reports |
|
|
Originally presented at the Water 99 Joint Congress--Brisbane, Australia, July 6-8, 1999
Commonly used methods for estimation of pumping-induced stream depletion are based on a series of idealistic assumptions about the stream-aquifer interface. In many cases, however, these assumptions are not consistent with field conditions. In order to obtain stream-depletion estimates that are based on assumptions more appropriate for conditions often faced in the field, a new analytical model is proposed. This model, which incorporates the effects of finite stream width, shallow stream penetration, and a low permeability streambed, is based on the Dupuit assumptions and a steady-state representation of flow across the streambed. A general solution for Stream depletion is developed in Laplace space and numerically inverted to obtain stream depletion as a function of time. In two special cases, the Laplace-space solution can be analytically inverted to obtain closed-form expressions. This solution is used to assess the impact of finite stream width, shallow stream penetration, and a low-permeability streambed on stream depletion estimates.
The evaluation of pumping-induced stream depletion is a critical step in the design of watershed-scale management plans. In the United States and many other countries, stream depletion estimates are commonly obtained for water-management design and water-rights adjudication purposes using analytical solutions based on simplified representations of the stream-aquifer interface (e.g., Theis [1], Glover and Balmer [2]). In particular, a graphical method for estimation of stream depletion developed by Jenkins [3] has seen much use. These analytical solutions and the estimation methods developed from them are based on a series of idealistic assumptions that include a fully penetrating stream and a perfect hydraulic connection between the stream and the aquifer. Although hydrogeologists have long recognized that these assumptions often bear little resemblance to reality, the method of Jenkins is still the most commonly used tool for estimation of stream depletion in many countries because of its simplicity and the lack of convenient-to-use alternatives.
In the last several decades, much new light has been shed on the concept of stream depletion (e.g., [4]). Carefully performed field studies have revealed the heterogeneous nature of the stream-aquifer interface and emphasized the impact of partial penetration (e.g., [3,5-8]). These field studies have been supplemented by a number of modeling investigations of stream-aquifer interactions. Several studies have numerically explored the impact of a number of factors on stream depletion estimates [9-12]. This work found that neglect of partial penetration and an imperfect hydraulic connection between the stream and the aquifer can result in a significant overestimation of stream depletion. Recently, the influence of these factors was illustrated using a simplified analytical model of stream depletion from a partially penetrating, infinitely thin stream [13].
Although largely unknown outside of Eastern Europe, a considerable amount of work was done on stream-aquifer interactions in the former Soviet Union. In particular, analytical solutions that incorporate a simplified representation of an imperfect hydraulic connection and a partially penetrating stream were developed [14-15] and have been widely used for well-field design and the analysis of stream-aquifer interactions [16-19]. The work of Grigoryev [14] and Bochever [15] will be the basis of the definition of the model of the stream-aquifer interface used here.
The primary objectives of this study are to: (1) obtain an analytical solution to a model of stream-aquifer interactions that incorporates a more realistic representation of the stream-aquifer interface; (2) explore the sensitivity of stream depletion estimates to various hydrogeological parameters; and (3) to demonstrate the difference between stream depletion estimates obtained with this model and those obtained using models based on more simplistic representations of the stream-aquifer interface.
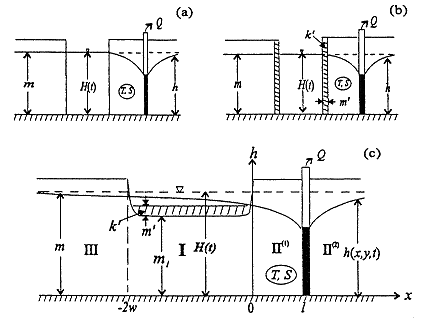
A major objective of this work is to develop methods for the estimation of pumping-induced stream depletion that are based on a model of stream-aquifer interactions that represents conditions typically found in the Great Plains region of the United States. Figures 1a and 1b depict conditions assumed in the commonly used models for estimation of stream depletion. Figure 1a represents the situation in which the stream fully penetrates and is in perfect hydraulic connection with the adjacent aquifer [1-3]. Figure 1b is an extension of the fully penetrating stream model to incorporate an imperfect hydraulic connection produced by low-permeability streambed sediments, a configuration that was examined by Hantush [20]. Unfortunately, Figures 1a-1b are often not representative of alluvial valleys in the Great Plains, where shallow stream penetration and large stream width-to-depth ratios are the norm.
In this work, we will develop a method for estimation of stream depiction that is based on a model of stream-aquifer interactions that incorporates shallow stream penetration and large stream-width-to-depth ratios (Figure 1c). The approach we utilize was originally proposed by Grigorvev [14] for the design of well fields in alluvial aquifers. The proposed approach involves dividing the aquifer into three zones (Figure 1c): Zone I, which includes both the stream-aquifer interface and the portion of the aquifer under the stream; Zone II, which consists of a section between the stream and the pumping well (II(1)) and a section on the opposite side of the well extending away from the stream (II(2)); and Zone III, which is located on the opposite side of the stream from the pumping well. The following series of assumptions are adopted in order to obtain an analytical solution for this configuration: (1) the stream is infinitely long in the horizontal plane and has low sinuosity; (2) the aquifer is homogeneous, isotropic and semi-infinite in lateral extent; (3) the stream and the aquifer are initially at hydraulic equilibrium, and the water table is initially horizontal at some level ho; (4) the streambed partially penetrates the aquifer with a hydraulic conductivity much less than the aquifer; (5) drawdown is small compared with the saturated thickness so the Dupuit approximation is applicable; (6) leakage across the streambed (to or from the stream) is vertical and occurs only through the stream bottom, and the stream and aquifer are hydraulically connected (albeit imperfectly) in all parts of the streambed; (7) groundwater in Zone I is under confined conditions while groundwater in Zones II and III is unconfined; and (8) stream stage does not affect stream depletion.
Figure 1. Hydrogeological conditions near the stream-aquifer interface: (a) hilly penetrating stream by Theis [1], Glover and Balmer [2], and Jenkins [3]; (b) fully penetrating stream by Hantush [20]; (c) partially penetrating stream with low permeability streambed by Grigoryev [14] and Bochever [15].
Consider hydraulic head h(x, y, t) in an aquifer with the aquifer base as a reference level, and a stream stage H(t) with the same reference level. Two-dimensional groundwater flow can be described by the following boundary value problem:
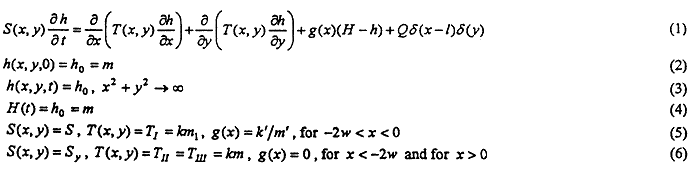
Here, x and y are Cartesian coordinates, t is time, k is
hydraulic conductivity of the aquifer, k' and m' are the hydraulic conductivity
and the thickness of the streambed, respectively; w is the half-width of the stream,
TI and S are transmissivity and storativity of Zone I, respectively,
TII and TIII are transmissivities for Zones II and III, Sy
is the specific yield, l is the distance from the well to the stream bank, Q is pumping
rate, ![]() is the Dirac function,
and m and ml are aquifer thicknesses for Zones II-II and Zone I, respectively (Figure 1c).
is the Dirac function,
and m and ml are aquifer thicknesses for Zones II-II and Zone I, respectively (Figure 1c).
Continuity conditions for head and flux are required along the vertical interfaces between Zones I, II, and III (lines x=0 and x=-2w).
We are interested in finding the stream depletion q(t) which can be expressed as

The introduction of dimensionless variables
![]() = x/w,
= x/w,
![]() = y/w,
t = TIIt)/(SyW2),
= y/w,
t = TIIt)/(SyW2),
![]() = S/Sy,
= S/Sy,
![]() = TI/TII
= TI/TII
![]() m1/m,
and
m1/m,
and ![]() = (k'W2)/(m'TII)
allows the problem to be rewritten in a dimensionless format, where
= (k'W2)/(m'TII)
allows the problem to be rewritten in a dimensionless format, where
![]() will be henceforth called stream leakance. In dimensionless variables, the equation (7)
for stream depletion can be rewritten as:
will be henceforth called stream leakance. In dimensionless variables, the equation (7)
for stream depletion can be rewritten as:
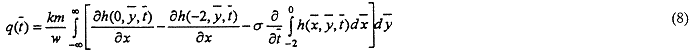
Due to the linearity of the boundary value problem (1) - (6), the solution for q(t) can be obtained using integral Laplace transforms [21]. Derivation of the solution in Laplace space for both stream depletion and drawdown is straightforward following the earlier proposed approach [15, 22], albeit tedious. In the general case, the solution for stream depletion can be numerically inverted using the Stehfest [23] algorithm with sixteen weighting coefficients.
The Laplace space solution for the general case, as well as analytical expressions for two simplified cases for which the inversion can be readily performed analytically, are given below.
The Laplace transform solution for the stream depletion is as follows:
where
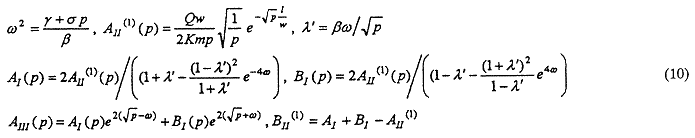
In this case, ![]() ,
and the analytical solution for stream depletion can be obtained in closed form [15, 21]:
,
and the analytical solution for stream depletion can be obtained in closed form [15, 21]:
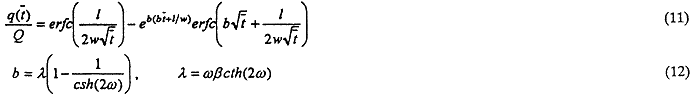
In this case, there is no Zone III, and
![]() .
The closed form analytical solution for stream depletion is:
.
The closed form analytical solution for stream depletion is:

Analysis of the solutions (9), (11) and (13) was performed using an example of a stream
with characteristics typical of many alluvial aquifers in the Great Plains region of the
United States. Consider a shallow stream which does not penetrate an unconfined aquifer
with the following parameters: hydraulic conductivity k = 20 m/day, aquifer thickness
m = mi = 10 m (i.e. ![]() = 1),
storativity S = 0.001, specific yield Sy = 0.2, stream width 2w = 10 m,
hydraulic conductivity of the streambed k' = 0.1 m/day, streambed thickness m' = 0.1 ,
and a pumping rate Q = 1000 m3/day from a well located at a distance l = 100 m
from the right bank of the stream. Using typical ranges for these parameters, one can
evaluate their influence on stream depletion estimates with the proposed model.
= 1),
storativity S = 0.001, specific yield Sy = 0.2, stream width 2w = 10 m,
hydraulic conductivity of the streambed k' = 0.1 m/day, streambed thickness m' = 0.1 ,
and a pumping rate Q = 1000 m3/day from a well located at a distance l = 100 m
from the right bank of the stream. Using typical ranges for these parameters, one can
evaluate their influence on stream depletion estimates with the proposed model.
The simplified solutions for stream depletion (11) and (13) were obtained by neglecting
the compressibility in Zone I (![]() = 0).
The accuracy of these solutions can be demonstrated by comparison with the numerical
inversion of (9). The same response was calculated from (9) using a range of a values from
0.005 to 1 by changing storativity S from 0.001 to 0.2 while keeping Sy fixed.
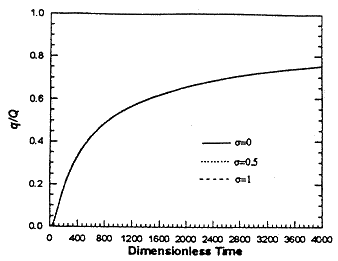
The results displayed in Figure 2 show that there is little dependence on
= 0).
The accuracy of these solutions can be demonstrated by comparison with the numerical
inversion of (9). The same response was calculated from (9) using a range of a values from
0.005 to 1 by changing storativity S from 0.001 to 0.2 while keeping Sy fixed.
The results displayed in Figure 2 show that there is little dependence on
![]() . Therefore, the storativity of the
confined aquifer in Zone I can be neglected for practical purposes.
. Therefore, the storativity of the
confined aquifer in Zone I can be neglected for practical purposes.
Figure 2. Effect of compressibility in Zone I
The Glover and Balmer [2] model of stream depletion for fully penetrating stream can be written as:

where ![]() = (km)/Sy is the
aquifer diffusivity. The Hantush [20] model, which adds a vertical low-permeability
streambed to the fully penetrating stream model of Glover and Balmer, can be written as:
= (km)/Sy is the
aquifer diffusivity. The Hantush [20] model, which adds a vertical low-permeability
streambed to the fully penetrating stream model of Glover and Balmer, can be written as:
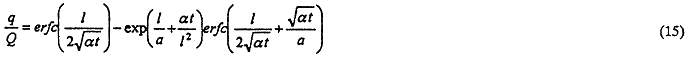
where a = k'm'/k is a retardation coefficient to incorporate the effects of the reduced permeability of the streambed (6).
In order to assess the impact of stream width and to compare our solution with these previous models, equation (11) is rewritten in dimensional form as follows:
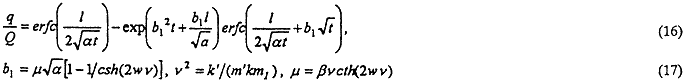
Figure 3 displays dimensional stream depletion plots from equations (14)-(16), along with the expression for the case of an infinitely wide stream (13). The results illustrate that with an increase of stream width, stream depletion becomes larger. In this particular example, there is no further increase in stream depletion for streams wider than approximately 30 m and the curves are very close to the curve for stream of infinite width. These results indicate that, for a given hydraulic conductivity and thickness of streambed, the effect of increases in the stream width becomes limited due to increases in the length of the groundwater flow path under the stream. In this case, the transmissivity of Zone I becomes the limiting parameter, and stream depletion is lower than in fully penetrating case. Interestingly enough, the Hantush solution corresponds to a relatively wide stream. Naturally, the largest values for stream depletion are obtained with the fully penetrating stream model. In certain conditions, dependence on the fully penetrating stream model can lead to significant overestimates of stream depletion.
Figure 3. Comparison of stream depletion for available solutions for various stream widths
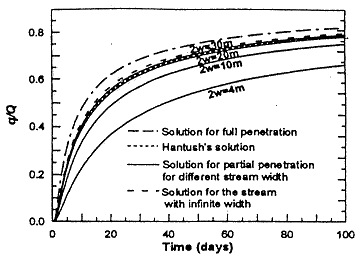
Stream depletion strongly depends on the value of the stream leakance parameter.
Figure 4 indicates that an increase in ![]() enhances the pumping-induced stream depletion. When the stream
leakance is large (
enhances the pumping-induced stream depletion. When the stream
leakance is large (![]() >> 1), the stream depletion curves approach the case of a fully penetrating
stream. Physically, case (
>> 1), the stream depletion curves approach the case of a fully penetrating
stream. Physically, case (![]() >> 1) corresponds to a very good hydraulic connection between
the stream and aquifer. In this situation, heads in both the stream and the
aquifer are very close, and the fully penetrating stream model becomes
applicable.
>> 1) corresponds to a very good hydraulic connection between
the stream and aquifer. In this situation, heads in both the stream and the
aquifer are very close, and the fully penetrating stream model becomes
applicable.
Figure 4. Effect of the leakance ![]() on stream depletion
on stream depletion
The commonly used analytical model of Glover and Balmer [2] and its extension by Hantush [20] disregard the effects of stream width and shallow penetration on stream depletion estimates. A new analytical solution, which is an extension of earlier work of Grigoryev [14] and Bochever [15], has been developed to explicitly consider these features. This solution incorporates the effects of stream width, the hydraulic conductivity and thickness of the streambed, and very shallow penetration. Evaluation of the solution indicates that stream depletion estimates are insensitive to the storage properties of the sub-stream aquifer zone, thereby significantly simplifying the required calculations. This evaluation also indicates that stream depletion estimates are very sensitive to the stream leakance parameter, which incorporates the effects of stream width, and the hydraulic conductivity and thickness of the streambed. As shown here, the larger the value for the stream leakance parameter, the more closely stream depletion estimates correspond to those for a fully penetrating stream. Note that all the results presented here assume that the Dupuit assumptions are valid.
The expressions presented here allow stream depletion estimates to be obtained that are more reflective of actual field conditions in many parts of the world. If these expressions are to be utilized for water-management design and water-rights adjudication purposes, field methods need to be developed for the estimation of the stream leakance parameter. Current theoretical and field studies at the University of Nebraska and the Kansas Geological Survey are being directed towards this goal.
[1] Theis, C.V., 1941, The effect of a well on the flow of a nearby stream, Trans. Am. Geophys. Union, 22(3), 734-738.
[2] Glover, R.E., and G.G. Balmer, 1954, River depletion resulting from pumping a well near a river, Trans. Am. Geophys. Union, v. 35, 468-470.
[3] Jenkins, C. T., 1968, Techniques for computing rate and volume of stream depletion by wells, Ground Water, 6(2), 37-46.
[4] Winter, T., 1995, Recent advances in understanding the interaction of groundwater and surface water, Reviews of Geophysics, Supplement, July. U.S. National Report to International Union of Geodesy and Geophysics 1991-1994, 985-994.
[5] Moore, I.E., and C.T. Jenkins, 1966, An evaluation of the effect of groundwater pumpage on the infiltration rate of a semipervious streambed, Water Resour. Res. 2(4), 691-696.
[6] Moench, A.F., V.B. Sauer, and M.E. Jennings, 1974, Modification of routed streamflow by channel loss and base flow, Water Resour. Res., 10(5), 963-968.
[7] Sophocleous, M.A., M.A. Townsend, L.D. Vogler, T.J. McClain, E.T. Marks, and G.R. Coble, 1988, Experimental studies in stream-aquifer interaction along the Arkansas River in Central Kansas--Field testing and analysis, J. Hydrology, v. 98, 249-273.
[8] Meigs, L.C., and J.M. Bahr, 1995, Three-dimensional groundwater flow near narrow surface water bodies, Water Resour. Res., 31(12), 3299-3307.
[9] Pinder, G.F., and S.P. Sauer, 1971, Numerical simulation of flood wave modification due to bank storage effects, Water Resour. Res., 7(1), 63-70.
[10] Spalding, C.P., and R. Khaleel, 1991, An evaluation of analytical solutions to estimate drawdowns and stream depletions by wells, Water Resour. Research, 27(4), 597-6 1 0.
[11] Sophocleous, M.A., A. Koussis, J.L., Martin, S.P. Perkins, 1995, Evaluation of simplified stream-aquifer depletion models for water rights administration, Ground Water, 33(4), 579-588.
[12] Conrad, L.P. and M.S. Beljin, 1996. Evaluation of an induced infiltration model as applied to glacial aquifer systems. Water Resour. Bull., 32(6), 1209-1220.
[13] Hunt, B., 1999, Unsteady stream depletion from ground-water pumping, Ground Water, 37(1), 98-102.
[14] Grigoryev, V. M., 1957, The effect of streambed siltation on well-field yield in alluvial aquifers, Water Supply and Sanitation, No. 6, 110-118, in Russian.
[15] Bochever, F.M., 1966, Evaluation of well-field yield in alluvial aquifers: The impact of a partially penetrating stream, Proceedings of VODGEO (Hydrogeology), No. 13, 84-115, in Russian.
[16] Shestakov, V. M., 1965, Theoretical Foundations of Evaluation of Afflux and Drainage, Moscow State University Press, 234 p., in Russian.
[17] Minkin, E.L., 1973, Groundwater-Surface Water Interactions and Their Role in Solutions of Problems of Applied Hydrogeology, Stroyizdat Press, Moscow, 104 p., in Russian.
[18] Vasilyev, S.V., N.N. Verigin, G.A. Razumov, B.S. Sherzhukov, 1975, Losses from Surface Water Reservoirs, Kolos Press, Moscow, 305 p, in Russian.
[19] Zlotnik, V.A., M. Kalinin, V. Usenko, and M. Cherepansky, 1985, Forecasting Groundwater Use Influence on the Hydrogeological Environment. Nauka i Technika Press, Minsk, USSR, 296 p., in Russian.
[20] Hantush, M.S., 1965. Wells near streams with semi-pervious beds, J. Geophys. Res., 70(12), 2829-2838.
[21] Carslaw, H.S., and Jaeger, J.C., 1959, Conduction of Heat in Solid, Oxford University Press, London, 510 p.
[22] Butler, J.J., Jr., and Liu, W.Z., 1991, Pumping tests in non-uniform aquifers: The linear strip case, J. Hydrology, v. 128, 69-99.
[23] Stehfest, H., 1970, Numerical inversion of Laplace Transforms, Commun. ACM, 13(1), 47-49.