Kansas Geological Survey, Subsurface Geology 12, p. 45-46
by
Allen W. Archer
Kansas State University
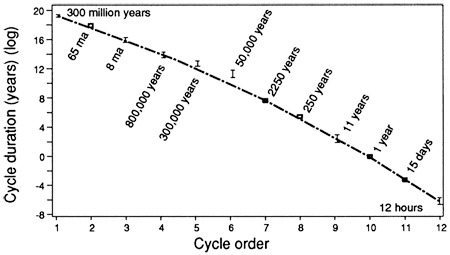
Detailed analyses of millimeter-scale laminations within tidal rhythmites from Carboniferous strata of Indiana, Illinois, Iowa, Kansas, and Colorado reveal a hierarchy of recognizable periodicities (Kvale et al., 1989). These periodicities are manifested by systematic changes in laminae thickness. Cycles contained within rhythmites, which occur in carbonate mudstones and siliciclastic shales, siltstones, and sandstones, can be related to an ordering of tidal periodicities. Consistency of these patterns through as much as 6 in of vertically continuous section in one example indicates a strong extrinsic control on sedimentation. The significance of the patterns can be explained by using modern tidal data to model a sedimentologic regime in which tidal rhythmites can be formed. Spectral analyses of modern data aid in recognizing and predicting tidal events which, from smallest to largest scale, include: 1) diurnal to semidiurnal tides related to the earth's rotation, 2) neap-spring patterns related to the lunar orbit, 3) tropical-equatorial tides related to lunar declination and distance, 4) solstitial-equinoctial tidal patterns related to the earth's orbit and axial tilt, and 5) yearly patterns related to seasonal parameters. Thus, such cyclic patterns represent the highest frequency oscillations of sea level observable within the rock record (fig. 1). Vertical continuity of the patterns indicates that sedimentation rates exceeding 1 m (3.3 ft)/year were attained during deposition of these laminated sediments and that such sections exhibit a very high degree of stratigraphic completeness (Archer and Kvale, 1988).
Figure 1--Spectrum of geological cycles; durations of higher-order cycles (1st through 6th) derived from various sequence-stratigraphic sources. Intermediate order cycles (2,250 and 250 yrs) are inferred; 11-yr cycle is average sunspot cycle, and lowest order cycles are related to tidal deposition.

Factors controlling modern tides are exceedingly complex but are related ultimately to the gravitational effects of the moon and sun upon the oceans of the earth. Each order of tidal periodicity in turn can be related to the earth's rotation, lunar orbit and declination (angle of lunar orbit to earth's equatorial plane), distance of the moon from the earth (apogean-perigean effects), and earth's orbit and solar declination (position of sun relative to earth's equatorial plane). Because these periodicities are not completely in phase, their interaction results in a recognizable hierarchy of patterns.
The smallest-scale (first-order) tidal patterns are produced by the earth's daily rotation relative to the gravitational effects of the moon and sun. A tidal bulge forms within the oceans and sweeps around the earth with a periodicity consisting of a stronger 12.42-hour component (lunar effects) and a weaker 12-hour component (solar effects). Thus, this bulge ideally has a twice daily, or semidiurnal, affect on the oceans of the earth.
Second-order patterns can be compared to cycles produced by tidal effects created by the periodicity of the lunar orbit, which is completed every 29.5 days. The earth, moon, and sun are aligned when the moon is either in a new or full phase. During these times, the gravitational effects of the moon and sun are combined and the highest, or spring, tides occur. Conversely, during the half-moon phases, the secondary gravitational effects of the sun offset lunar effects to produce the lowest, or neap, tides. Neap-spring cycles occur every 14.75 days and two such cycles occur during one lunar orbit (lunar month).
Third-order tidal patterns are related to the moon's declination, which is the angle of the lunar orbit to the earth's equatorial plane, and also by the distance of the moon from the earth. For example, the time required for the moon to change declination from zero (over the earth's equator) to the maximum of 28° (over the tropics) and then back to zero is 13.66 days. During the time when the moon crosses the equator, or "crossover," the semidiurnal inequality is minimized. Therefore the two semidiurnal tides produced during a crossover are approximately equal in height. Conversely, when the moon is at its maximum declination, the semidiurnal inequality is maximized. Because the crossover period is less than the interval between spring tides (14.75 days) described above, crossovers will occur about one day earlier within each successive neap-spring cycle.
The yearly cycle of seasons on the earth is related to the earth's axial tilt of 23.5°. Fourth-order patterns can be related to solstitial and equinoctial tides. In modern environments tidal ranges are maximized during the solstices (June and December), which is also the time of maximal semidiurnal inequality of the tides. An opposite effect occurs during the equinoxes (March and September) when the semidiurnal inequality is at a minimum. During the equinoxes, dominant tides are approximately equal to subordinate tides.
Yearly sea-level variations also occur across most of the oceans. Direct astronomical effects are in part responsible for yearly sea-level change; however, the fluctuation is equated more directly to seasonally varying parameters such as temperature, salinity, and air pressure. Maximum yearly sea-level occurs in different parts of the world during different seasons. Thus tidal patterns in such areas will exhibit yearly fluctuations in tidal heights superimposed upon all the previously discussed, smaller scale patterns.
Tidal cyclicity preserved in the rock record can be used to estimate sedimentation rates. Estimates of deposition rates of about 1 m (3.3 ft)/year within Carboniferous tidalites are based upon thicknesses of semidiurnally emplaced laminae, occurrence and thickness of neap-spring cycles, and interpretation of larger scale yearly cycles. These high rates of sedimentation are supported by other observations, such as occurrence of upright lycopod trunks.
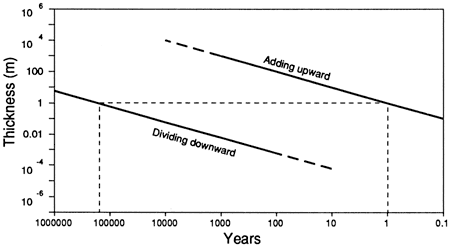
The nearly continuous record of semidiurnal deposition for several years bears greatly on concepts of "stratigraphic completeness" (Sadler, 1981). Not only has a detailed, multi-yearly record of daily sedimentation been preserved, but also extremely high rates of sedimentation have been documented. Although such rates probably were achieved only locally and may be related to compaction of underlying sediments, the recognition of such rates poses some potential problems with the delineation and correlation of longer term (10,000-100,000-yr) cycles on either a local or regional scale. Rates of sedimentation based upon detailed laminae measurements are orders of magnitude more rapid than rates derived by dividing formational thickness by formational time. For example, tidalites within the Mansfield Formation of Indiana have determinable rates of accumulation as high as 1 m (3.3 ft)/year; however, dividing formational time (about 15 Ma) by formational thickness (about 90 m [297 ft]) yields rates of about 1 m (3.3 ft) per 160,000 years. At least within these localized tidal deposits, formational time divided by formational thickness will yield depositional rates that are many orders of magnitude slower than those indicated by detailed sedimentological analyses (fig. 2). Such comparisons support a view of the rock record in which short-term episodes of rapid sedimentation are punctuated by long periods of nondeposition. Thus delineation of short- and long-term cycle durations becomes extremely problematic without reasonable sedimentological constraints.
Figure 2--Differences in estimating lengths of time for deposition of the Mansfield Formation (Pennsylvanian) of Southwestern Indiana. Line labeled "adding upward" based upon rates of sedimentation derived from analyses of daily, biweekly, and yearly tidal cycles. Conversely, line labeled "dividing downward" is based upon average long-term rates derived by dividing total formational thickness by total formational time. For 1 m (3.3 ft) of sediment, the two techniques yield rates that differ by over five orders of magnitude.
Archer, A. W., and Kvale, E., P., 1988, Ultimate resolution of transgressive-regressive stratigraphic units--a theoretical discussion based upon the Carboniferous of the Illinois basin: Geological Society of America, Abstracts with Programs, v. 20, p. 327-328
Kvale, E. P., Archer, A. W., and Johnson, H. R., 1989, Daily, monthly, and yearly tidal cycles within laminated siltstones of the Mansfield Formation (Pennsylvanian) of Indiana: Geology, v. 17, p. 365-368
Sadler, P. M., 1981, Sediment-accumulation rates and the completeness of stratigraphic sections: Journal of Geology, v. 89, p. 569-584
Kansas Geological Survey
Comments to webadmin@kgs.ku.edu
Web version May 11, 2010. Original publication date 1989.
URL=http://www.kgs.ku.edu/Publications/Bulletins/Sub12/Archer/index.html