Kansas Geological Survey, Ground Water Series 4, originally published in 1982
Next Page--Appendices
Originally published in 1982 as Kansas Geological Survey Ground Water Series 4. This is, in general, the original text as published. The information has not been updated.
Because of its abundance of land and water, Kansas has long been one of America's most productive agricultural states. Individual farmers have been effectively managing these resources to serve their short-term economic purposes. However, no long-range management plan has existed for groundwater, the major source of irrigation water in western Kansas; because of this the availability groundwater is declining noticeably. In particular areas, the decline is so large that irrigators have been forbidden to drill additional wells.
This study demonstrates the use of modern computer-modeling techniques in the management of a limited resource such as groundwater in some areas of Kansas. The Pawnee Valley in south-central Kansas was chosen because it has shown a large decline in groundwater availability. A mathematical model was developed to study the effects of various management options on the groundwater in the Pawnee Valley. The results of applying this model to conditions in the Pawnee Valley provide a guide for managing groundwater resources over the next 10 years.
The basic conclusion of this study is that the groundwater resources in the Pawnee Valley are highly over-appropriated and some action by the irrigators must be taken to slow down the rate of depletion. It must be kept in mind that the computational results in this report need to be applied with caution and considerable judgment, because of the inherent assumptions that exist in any groundwater management model and the data used in it. The results of this study are intended as a guide rather than as an absolute.
A groundwater management model based on the linear-systems theory and on the use of linear programming is formulated and solved. The model maximizes the total amount of groundwater that can be pumped from the system subject to the physical capability of the system and institutional constraints. The results are compared with analytical and numerical solutions. Then, this model is applied to the Pawnee Valley area of south-central Kansas. The results of this application support the previous studies about the future groundwater resources of the Valley. These results provide a guide for the groundwater-resources management of the area over the next 10 years.
For a long time Kansas has been blessed with natural resources that have helped to make it one of the most productive agricultural states in the United States. These resources, water and land, have been managed effectively by individual farmers to serve their short-term economic purposes. However, because of a lack of any long-range management plan, groundwater, the major source of irrigation water in western Kansas, is showing noticeable decline; and in particular areas, the decline is so large that a moratorium has been declared on further expansion of the number of irrigation wells.
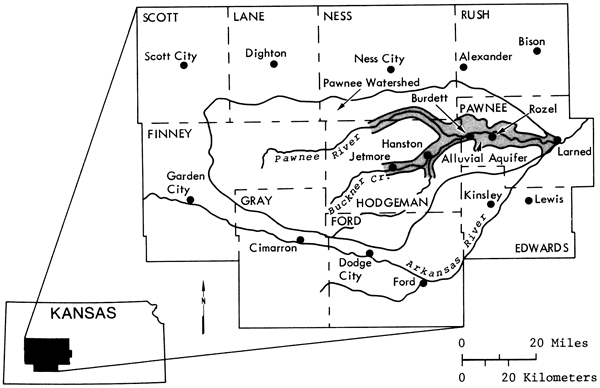
One of the areas that has shown considerable decline in groundwater levels is the Pawnee Valley, located in south-central Kansas (Fig. 1). For the last two years the Geohydrology Section of the Kansas Geological Survey has been studying the groundwater resources of this area, resulting in this report, as well as another previously published report (Sophocleous, 1980). These studies were carried out in three phases.
Figure 1--Map showing the location of the study area (Pawnee Valley) in Kansas.
Phase 1: A hydrogeologic investigation of the Valley was conducted. All available data were reviewed and new water-level data were collected. Based on these data, conclusions were reached about the boundaries of the Valley, thickness of the water-bearing formation, physical properties of the formation, and the amount of lateral and vertical recharge to the aquifer.
A hydrologic budget analysis for the region revealed that the groundwater resources of the Valley have declined noticeably over the last 30 years, and many areas are already considered over-appropriated. It also showed that each year an average of 0.5 inch of water is recharged to the system, and almost six inches of water are withdrawn for irrigation. This mass imbalance has caused the present concern of some farmers about the future of their water resources (Sophocleous, 1980, 1981).
Phase 2: In this phase the results of the previous phase were quantified. These data were used in the calibration of a digital computer model. The equation that describes the flow of water through isotropic porous media is:
(1) ∇ · (T(
) ∇h(,t)) = S() (δh / δt) = Σj=1m Q(j)δ(-j)
where
T() = Transmissivity [L2/T]
h(,t) = hydraulic head at at time t [L]
S() = storativity or specific yield at (dimensionless)
Qj = magnitude of sink or source at j [L/T]
δ (-j = Dirac delta function
= coordinate of a point (x,y)
t = time [T]
M = total number of sinks or sources.
In terms of drawdown, equation (1) may be written as:
(1-a) ∇ · (T() ∇s(,t)) = S() (δs / δt) = Σj=1m Q(j)δ(-j)(T(x)
where s(,t) is drawdown at at time t (L].
Equation (1-a) is subject to the initial condition
s(,t) = 0
and boundary conditions
s(Γ,t) = 0 on Γ (i.e., constant head B.C.)
and (δs(Γ',t) / δn) = 0 on Γ' (i.e., constant flux B.C.).
n is the normal direction to the boundary, and Γ and Γ' are segments of the boundary where the appropriate condition applies. This equation is based on the continuity equation and Darcy's law.
Sophocleous (1980, 1981) used a two-dimensional finite-difference model developed by Knowles and others (1972) to identify the parameters of the aquifer K and S (i.e., calibration), and using the same model, he simulated the future water-table configuration of the aquifer as a result of six different options ranging from the continuation of the present rate of pumpage to a 20 percent increase and decrease in this amount. He also gave a detailed hydrogeologic description of the aquifer. The conclusions reached in that study were: a) the groundwater withdrawals in the Valley have caused substantial decline in the water table, b) the wet periods are very unlikely to reverse water-level declines, and c) a rather bleak future is indicated for groundwater supplies in a large part of the Valley unless the groundwater management districts of the area soon make important decisions regarding their water supply. Among these decisions, a freeze on new irrigation wells and the implementation of a depletion allowance of not more than 40 percent of saturated thickness are mentioned.
Phase 3: In this phase a management model was proposed that may be effective in the overall preservation of the Valley's future groundwater resources. Any groundwater management plan in Kansas must be based on the groundwater laws of Kansas. These laws are based on the doctrine of prior appropriation (i.e., the seniority of the water users in any management plan must be preserved). Naturally, the best management plan is the one that optimizes some objective function subject to a set of physical, economic, and legal constraints. One can formulate two types of plans: one plan may try to optimize some objective function based on an economic measure such as cost, gross return, or net return; the other plan may be based on the physical capability of the system to deliver the maximum quantity of water over a period of time subject to a series of physical, legal, and institutional constraints. This latter model was tested on the proposed area. In a future study, we plan to apply a model of the first kind to the area to evaluate the price elasticity of crops and energy on the optimal management policy.
In any optimal management model, an objective function is optimized subject to a set of constraints. Among the constraints, an equation of state that mathematically describes the transition of the state of the system from one stage to another must exist. For groundwater flow, the equation of state is presented in (1). Solution of this equation for non-homogeneous and anisotropic systems has been achieved numerically. The result of this solution is a set of values specifying hydraulic heads or drawdowns at each designated point in the system as a result of a given set of pumpage rates. However, when the pumpage is unknown, as is the case in a management model, equation (1) becomes indeterminant.
In order to present an equation of state based on (1), which can be used in a management model, Maddock (1972) proposed the use of linear systems theory. Other investigators (Dreizin, 1975; Moench and Kisiel, 1970; Venetis, 1971; Hall and Moench, 1972; Morel-Seytoux and Daly, 1975; Bathala and others, 1977) have also reviewed linear systems theory and have applied it to groundwater or groundwater-surface water systems. Recently Gorelick and Remson (1982) have applied the principle of linear-systems theory to the management of multiple groundwater pollutant sources in a steady groundwater region.
The basic theorem that makes linear systems analysis applicable to water resources systems is the convolution integral or the superposition integral:
(2) s(t) = ∫0t Q(τ) B(t-τ) dτ
where
Q(t) = system input (system stress such as pumpage)
B(t) = system unit impulse response function
s(t) = system output (system response such as drawdown)
t = time
τ = dummy variable.
The convolution integral is applicable to linear systems (i.e., the boundaries and the equation of state do not change with time, and the superposition laws are applicable to them) (Cheng, 1959; Bear, 1979). Equation (2) formulates the system's equation of state in a linear cause and effect form. It has been applied to groundwater problems since 1935 when C. V. Theis (Theis, 1935) applied the solution of the heat-conduction equation based on this integral to the groundwater-flow equation.
Maddock (1972, 1974a) used linear-systems theory and Green's functions to arrive at the discrete form of (2) for a multi-well system consisting of M wells for n time periods:
(3) s(k,n) = Σj=1m Σi=1n q(j,i) β(k, j, n-i+1)
where
s(k,n) = drawdown at well k at time step n
q(j,i) = pumpage of well j during period i
β(k,j,n-i+1) = system unit response function or unit drawdown at well k as a result of unit pumpage at well j for the (n-i+1)th time period.
In (3) β(k,j,i) must be calculated analytically or numerically. Bathala and others (1977) lists analytical solutions for calculations of β's for different aquifer boundaries. Maddock (1972) obtained the β's using the numerical solution of the groundwater-flow equation while satisfying Neuman- and Dirichlet-type boundary conditions and variations in physical properties of the aquifer. The procedure proposed by Maddock is as follows: a) the domain is discretized; b) values of hydraulic parameters (storativity and transmissivity) are assigned to each discrete segment or node; c) the boundary conditions are identified and quantified for input to the model; d) the locations of wells are designated; e) starting from the first well to the last, a pumpage of one unit is assigned to that well for the first time step and zero units for the rest of the time steps; and f) the drawdowns calculated in this manner become the β's in (3).
In this study a computer program developed by Maddock (1974a), which uses the above procedure to generate the response functions, (βs), is used.
The use of the response function, β, to calculate drawdown in an aquifer may be demonstrated as follows. Consider a homogeneous, isotropic, confined, non-leaky aquifer of infinite extent with one fully penetrating well. The drawdown at a distance r from the well at time t is (Theis, 1935):
(4) s(r,t) = (Q / 4πT) ∫u∞ (e-v / v) dv
where
s(r,t) = drawdown at a distance r from well at time t
Q = constant discharge for the entire pumping period
v = dummy variable
u = r2s / 4Tt
S storativity coefficient
T transmissivity
t pumping period.
Then, following the procedure outlined above, for Q = 1, equation (4) for N time periods may be written as:
(5) α(r,i) = (1/rπ) ∫ui∞ (e-v / v) dv i = 1, 2, 3, . . . , N
where α(r,i) = unit drawdown at a distance r from well at the end of ith time step, ti, caused by one unit pumpage and ui = (r2s / 4Tti).
Bathala and others (1977) includes a schematic presentation for the solution of (4) using the superposition principle for three time steps with three different rates of pumpage (Fig. 2). To use (5) to calculate the drawdowns shown in Figure 2,
Let α0 = α(r,0) = 0
and βi= αi - αi-1 = α(r,i) - α(r, i-1).
Figure 2--Schematic representation of superposition principle. After Bathala and others (1977).
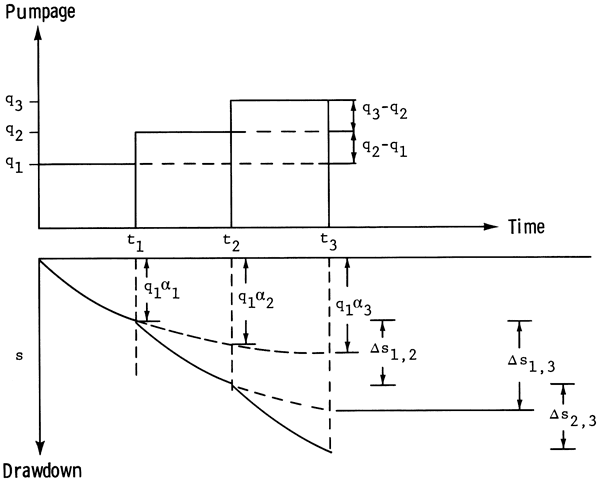
For t = 0 to t = t1 (with q = q1)
(6-a) s(r,t1) = q1α1 = q1(α1 - α0) = q1β1
For t = 0 to t = t2 (with q = q1 for 0 to t1, and q = q2 for t1 to t2)
(6-b) s(r,t2) = q1α2 + Δs1,2 = q1(α2 + (q2-q1)α1 = q1β2 + q2β1
For t = 0 to t = t3 (with q = q1 for 0 to t1, and q = q2 for t1 to t2, and q = q3 for t2 to t3)
(6-c) s(r,t 3) = q1α3 + Δs1,3 + Δs2,3 = q1α3 + (q2 - q1)α2 + (q3-q2)α1 = q1(α3 - α2) + q2(α2 - α1) + q3(α1 - α0) = q1β3 + q2β2 + q3β1
For N time steps, (6-c) may be written as:
(7) s(r,N) = Σi=1Nqiβ(N-i+1).
Maddock (1972) calls β the algebraic technological function or response function. Application of convolution integral (2) to groundwater aquifers is contingent upon the homogeneity of the boundary conditions. Any changes in the boundary conditions must be explicitly modeled by a capture term. A capture term may represent transpiration, leakage from a confining bed, or any other term that tends to modify the boundary conditions of the aquifer system. For unconfined aquifers where the free-surface boundary conditions change with time, one may try to derive the appropriate algebraic technological functions (Maddock, 1974b), or correct the drawdown obtained from equation (3) by a procedure proposed by Jacob (1944):
(8) s = s' - (s'2 / 2bZ)
where: s = drawdown in the confined aquifer
s' = drawdown in the unconfined aquifer
b = saturated thickness.
This relationship adjusts the drawdown in a confined aquifer, s, to that of an unconfined aquifer, s', rather effectively provided that s' is not excessive in comparison with b, the saturated thickness.
Based on the equation of state given in (3), several types of management models may be formulated. These models seek to optimize objective functions that are based on some economic criteria such as cost or net return. In this study an objective function based on the physical capability of the system is proposed. The problem to be solved is as follows:
(9-a) Max Q = Σk=1MΣn=1Nq(k,n)
subject to
(9-b) 0 < q(k,n) ≤ Q(
,n) for all k and n
(9-c) Σk=1Mq(k,n) ≥ 
(n) for all n
(9-d) 0 ≤ s(k,n) ≤ γb(k) for all k and n
(9-e) s(k,n) = Σj=1MΣi=1Nq(j,i) β(k,j,n-i+1)
where:
Q = sum of the pumpages of M wells for N time periods
q(k,n) = pumpage of well k during period n
(k,n) = upper limit of pumpage of well k during period n
(n) = lower limit of the sum of pumpages of M wells during period n
s(k,n) = drawdown of well k from the start of pumpage to the end of time period n
γ = a fraction 0 ≤ γ ≤ 1
b(k) = saturated thickness of well k before pumpage started
yb(k) = upper limit of drawdown for well k up to the end of period n.
Objective function (9-a) seeks to find the maximum quantity of pumpage from M wells for N time periods. Constraint (9-b) states that the pumpage of a well cannot be greater than the appropriated right of that well, (k,n). Constraint (9-c) states that the sum of the pumpages from M wells during any time period will not fall below a limit, (n). This limit, (n), may be chosen based on the minimum amount of water required to grow a crop with the least amount of water. Constraint (9-d) states that the drawdown in each well at any time will not exceed a limit, γb(k). In Kansas, this limit is normally set by the local groundwater management districts and is a fraction (i.e., γ < 1) of the saturated thickness, b(k) at a particular well, (k). Constraint (9-e) guarantees that the above process will also honor the continuity equation that describes the flow of water through porous media, equation (1). The response function, β, is calculated using a discrete form of equation (1) and a procedure, outlined above, developed by Maddock (1974a).
In order to avoid any confusion, it must be restated here that the so-called "optimal" net pumpage policies to be calculated by the above model are based on the physical parameters of the aquifer and on man-made constraints. These policies may or my not be related to a set of optimal policies based on some economic criteria.
The objective function (9-a) and constraints (9-b through 9-e) form a linear programming model that can be solved by any linear programming package. For each well there are two unknowns (q and s) at each time step. Therefore, for a system consisting of, say, 100 wells and 10 time periods, a total of 100 x 2 x 10 = 2000 unknowns exist. The linear programming package used in this study was developed by Murtagh and Saunders (1977).
In order to test the accuracy of the management model formulated above, three hypothetical cases were studied.
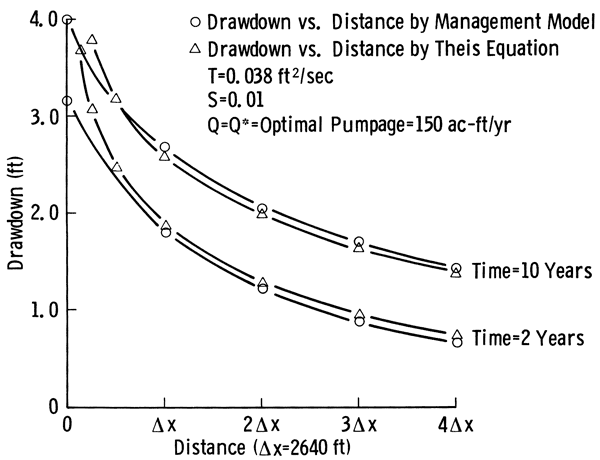
Case 1: Homogeneous and Isotropic Infinite Confined Aquifer--A homogeneous and isotropic confined aquifer of infinite extent with one fully penetrating pumping well in the middle was analyzed by the model and the optimal pumpages and associated drawdowns were calculated. In order to simulate infinity, the dimensions of the digital model were assumed large enough so that no boundary effects were noted at the well. Then the optimal pumpages were used in Theis' equation and a new set of drawdowns were calculated. Figure 3 shows the drawdown versus distance calculated by the management model and Theis' equation at the end of two and 10 years of pumpage. These graphs show good agreement for nodes away from the pumping well. For small distances from the well, the inaccuracies inherent in both analytical and numerical solutions appear, and agreement between the two graphs becomes less satisfactory as the distance becomes smaller. The error between the two graphs for points away from the well is directly attributed to grid spacing (Δx) used in the numerical model. The related data for this case are presented in Figure 3.
Figure 3--Comparison of drawdown versus distance curves of one well in a homogeneous and isotropic aquifer of infinite extent as obtained by the management model and Theis' equation.
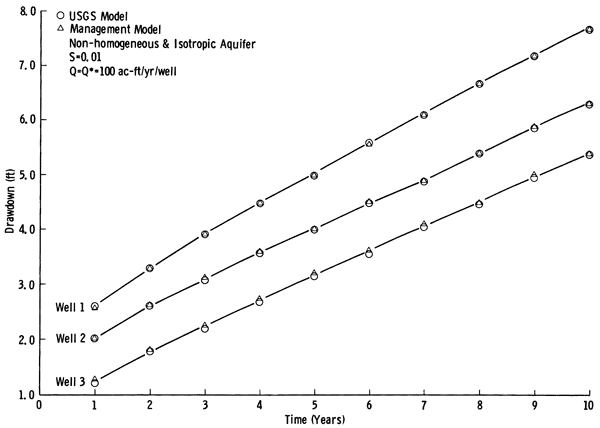
Case 2: Non-Homogeneous and Isotropic Confined Finite Aquifer--A nonhomogeneous but isotropic confined aquifer of finite extent with no-flow boundary conditions was analyzed by the management model for three wells. Since no natural discharge or recharge takes place, the existence of no-flow boundary condition does not create any capture term and thus the drawdown calculated by (2) is directly applicable. The optimal pumpages of 100 acre-feet/year were obtained together with the associated drawdowns. Then these pumpages were used in a digital groundwater model developed by the U.S. Geological Survey (Trescott and others, 1976) to calculate the drawdowns. Figure 4 shows plots of drawdowns versus time for the three wells by the management model and the U.S. Geological Survey's digital groundwater model. As observed, the data are distinguishable only at small times.
Figure 4--Comparison of drawdown versus time curves of three wells in a nonhomogeneous and isotropic aquifer as obtained by the management model and U. S. Geological Survey digital model.
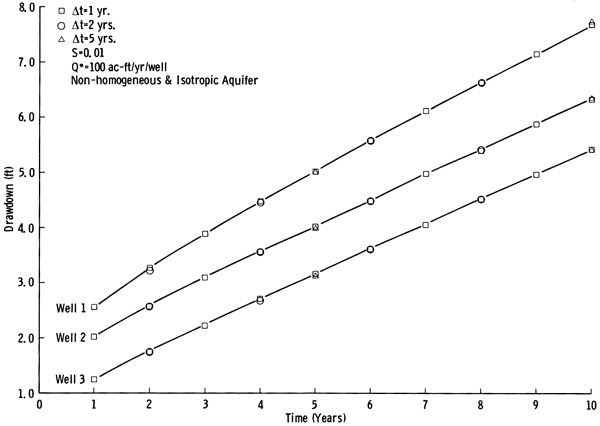
Case 3: Effect of Time Increment, Δt, on the Accuracy of Results--In this case the problem of Case 2 was analyzed by the management model with time increments Δt = 1, 2, and 5 years for a total of 10 years. Figure 5 shows the drawdown versus time for the same wells as obtained by the management model with different time increments. After five years of pumpage, very little difference in drawdown is observed among the three wells. This leads us to the conclusion that, if the intermittent data points are not needed, almost the same results are obtained with much less computation (10 time increments for Δt = 1 year versus two time increments for Δt = 5 years).
Figure 5--Comparison of the drawdown versus time for three pumping wells in a non-homogeneous and isotropic aquifer as obtained by the management model with different time steps.
The management model described above was applied to the Pawnee River Valley of south-central Kansas (Fig. 1), an area that seems rather well suited for its application. This is an area in which the need for such models exists and substantial hydrogeologic data have been collected and analyzed. A predictive numerical model has been calibrated for the area and used to simulate the expected future of the resource as a result of a given pumpage. The coefficient matrices of transmissivity and storativity and other data calculated in that calibration (Sophocleous, 1980) are used in the application of our management model.
Figure 6 shows the idealized boundary of the study area. Figures 7, 8, and 9 show the distribution of transmissivity, specific yield, and saturated thickness obtained for the area. In Figure 6 the boundary conditions used in this study are also specified, i.e., boundaries are to be considered as no-flow unless they are designated by CH, specifying a constant-head boundary.
Figure 6--Idealized boundary of the study area in the Pawnee Valley. CH = constant-head boundary.
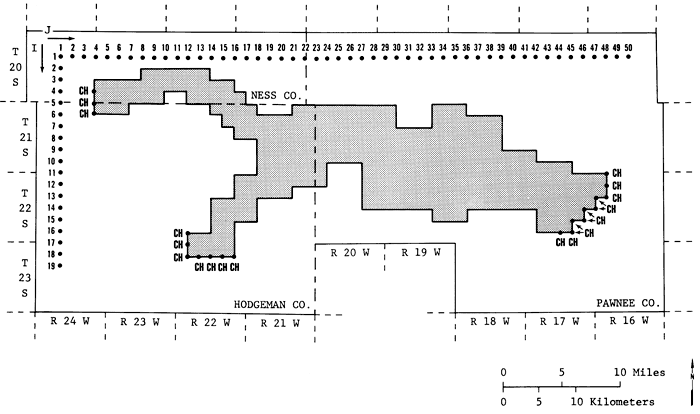
Figure 7--Transmissivity matrix (x 1000 ft2/sec) used in the calulation of β coefficients.
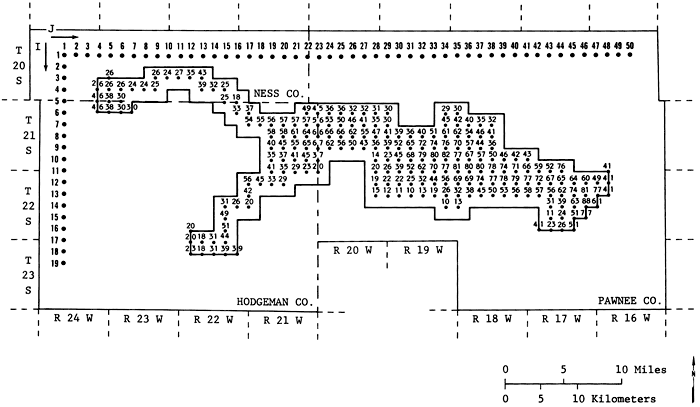
Figure 8--Percent specific yield used in the calulation of β coefficients.
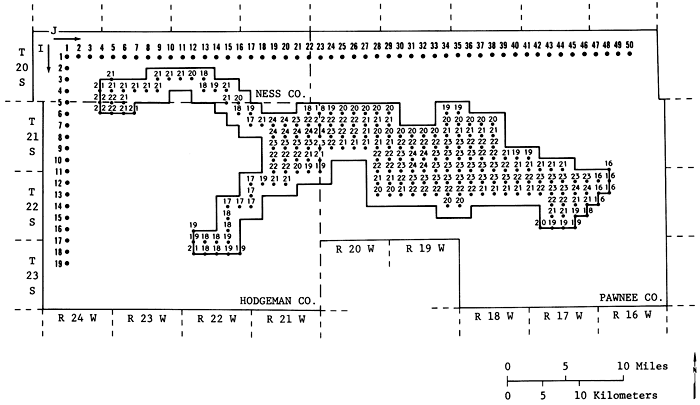
Figure 9--1979-80 saturated thickness (ft.) matrix used in the analysis.
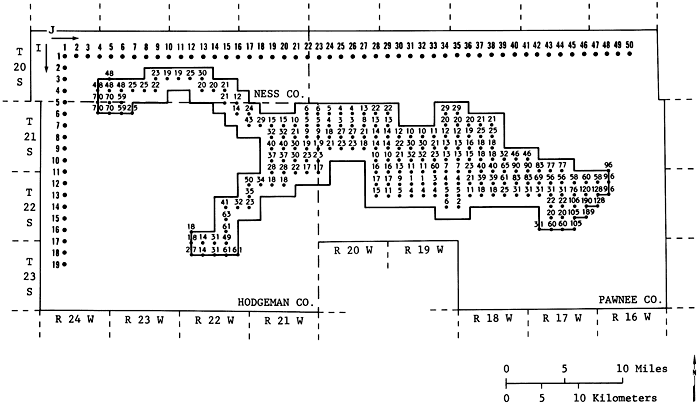
In order to evaluate the potential pumpage of the area, a number of well fields was designated in the area. Figure 10 shows the location of 61 hypothetical well fields in the area. Each hypothetical well field represents the total pumpage from several real wells in its vicinity. These locations were chosen after considerable investigation of the maximum number of well fields that can be handled efficiently by the computer program used in this study and of the size of the computer memory available (Honeywell 66/60 at The University of Kansas). This configuration of well fields is by no means the only configuration that can be used in this analysis. Had some other well-field configuration been chosen, the results probably would have been somewhat different. Another factor that affected the location of these hypothetical well fields was the amount of net appropriation in an area. "Net appropriation" is defined here as the difference between appropriation and recharge. If the amount of net appropriation in an area was high, more hypothetical well fields had to be located in that area. In Appendix A the amount of net appropriation to each well field is presented together with the 1979 saturated thickness at that well field. The net appropriation was calculated using 0.5 inch of recharge per year.
Figure 10--Location of the 61 hypothetical well fields int he study area.
Net appropriation at a well field (k) during a particular period of time (n), (k,n), is used in equation 9-b as the upper limit of pumpage. It is assumed that the net appropriation at each well field as given in Appendix A remains constant for each year of the analysis. This Appendix may not show the actual appropriated pumpages for some well fields. This is because, in designing a grid system such as the one presented in Figure 7, a decision had to be made as to what appropriation should be assigned to which grid point.
As was stated in the formulation of this problem, the saturated thickness at well field (k), b(k), plays an important role in the decision-making process. Equation (9-d) specifies how a portion of the saturated thickness, γb(k), is used as a constraint in the problem.
The lower limit of the sum of the pumpages for a time period, (n), in equation (9-c) was set equal to zero. In other words, we decided to allow the sum of the pumpages to vary from zero to any upper limit (optimum pumpage) as long as (9-b), (9-d), and (9-e) were satisfied.
Two time periods (five and 10 years) were used in the application of the management model to the Pawnee Valley. Annual optimal policies were calculated for a time period of five years and biennial optimal policies were calculated for a time period of 10 years. As the results show, many of the appropriations cannot be satisfied over these periods of time. Therefore, longer time periods were not considered in the analysis.
The model described above calculates the residual drawdown at a particular time and location. In order to calculate the remaining saturated thickness at the end of some time period, one should superimpose the drawdowns associated with that time period on the steady-state water-table condition at that time. However, obtaining a steady-state water-table condition for a valley that has been under pumpage stresses for a long time requires substantial simulation time with zero stress. one may turn off all the pumps, assume a known recharge rate, use the existing water table as the initial condition, and simulate the water-table configuration at a particular time. Depending on the length of simulation time, the simulated water table will be different from the initial water table and will approach the steady-state water table as the length of simulation time without stress increases.
To obtain the 1984 water table, the 1979 water table was used as the initial condition together with all the relevant data, 0.5 inch of recharge per year, and no pumpage in the calibrated model. Examination of the simulated water table indicated that this water table is a good approximation to the steady-state water table. Then, residual drawdowns were subtracted from this water table to obtain the remaining saturated thickness. In Appendix A the 1979 saturated thickness and the projected 1984 saturated thickness with zero pumpage are tabulated for the 61 well fields under investigation.
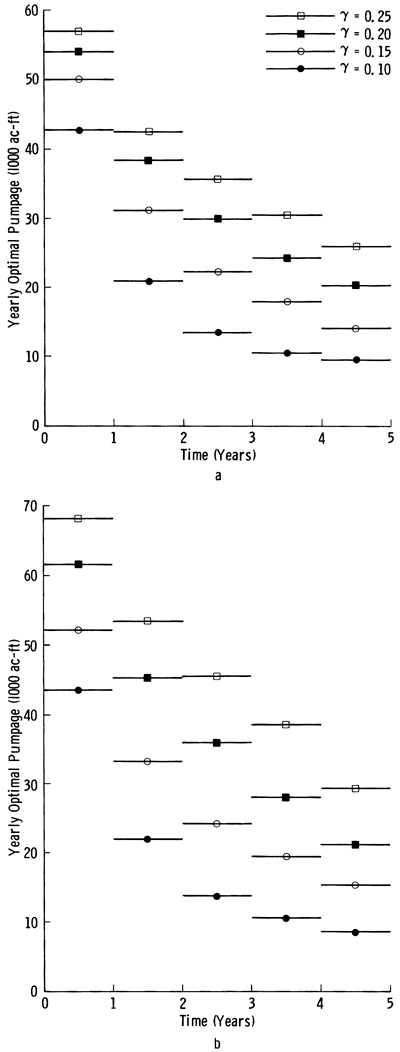
Based on data presented above and in Appendix A, four different yearly optimal pumpage policies were generated for a total time of five years. All yearly optimal pumpage policies used the same data except the percent usable saturated thickness, γ. The values of γ used were 25, 20, 15, and 10 percent of usable saturated thickness. These values of γ were chosen after a review of the management policies of the local groundwater management districts. When γ = 25, no more than 25 percent of the 1979-80 saturated thickness, as shown in Figure 9, may be depleted during the five-year period. Figure 11 shows the variation of five-year optimal net pumpage policies with γ. Figure 12a shows the yearly optimal pumpage policy as a function of time for different γ's.
Figure 11--Optimal five-year pumpage versus percentage usable saturated thickness with and without net appropriation as a constraint.
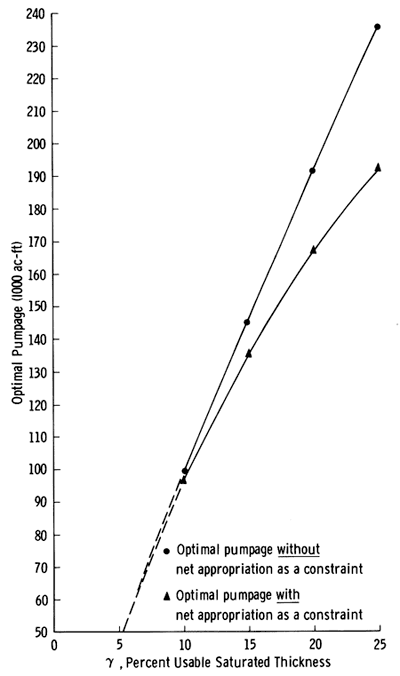
Figure 12--Optimal yearly pumpage versus time: a, with net appropriation as a constraint; b, without net appropriation as a constraint.
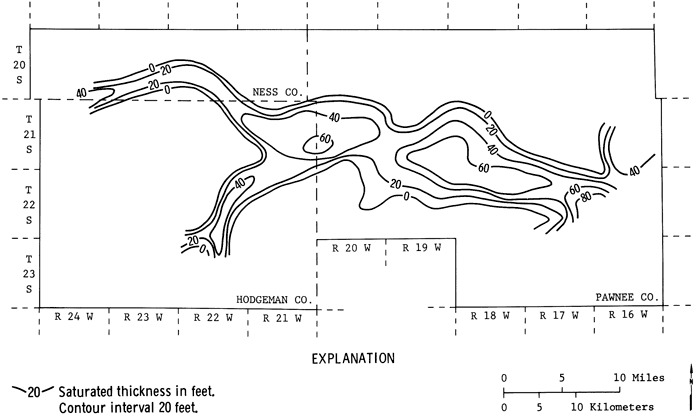
Appendix A lists the remaining saturated thicknesses at the end of the five years as a result of yearly optimal pumpage policies for different γ's. Figures 13a, b, and c show the 1979-80 saturated thickness, and the remaining approximate saturated thickness contours at the end of 1984 for γ = 25 and γ = 10 percent. From these figures the effects of different policies may be clearly observed. For γ = 25 percent the volume of the remaining saturated thickness is about 15 percent smaller than the volume of the saturated thickness for 10 percent.
Figure 13a--1979 saturated thickness map of the Pawnee Valley (after Sophocleous, 1980).
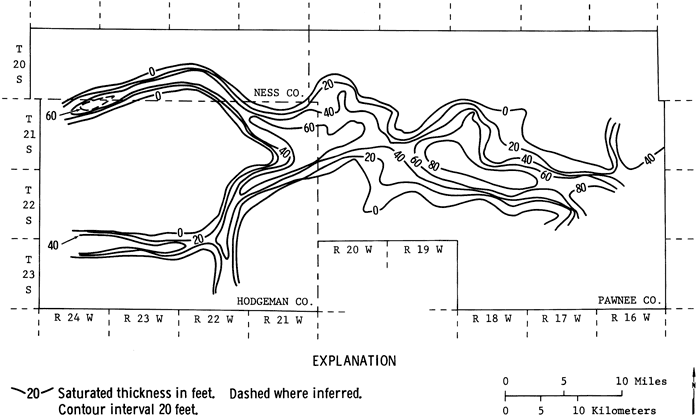
Figure 13b--1984 saturated thickness obtained by the management model for γ = 25 percent.
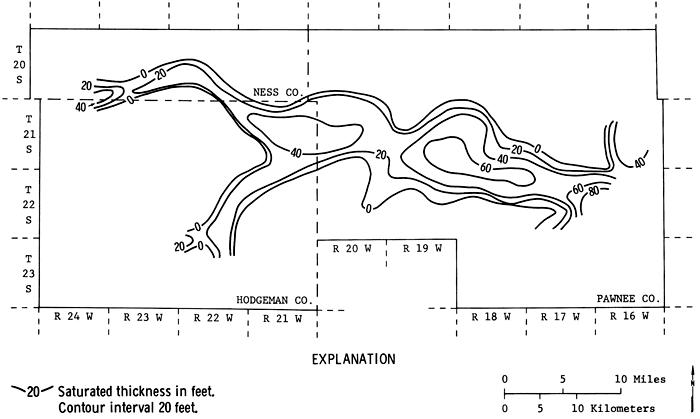
Figure 13c--1984 saturated thickness obtained by the management model for γ = 10 percent.
In Appendix B the distributed optimal pumpage policies are tabulated by year for each well field and different γ's, together with percentage of five-year net appropriation satisfied by this pumpage. The well fields that satisfy the net appropriation are shown. For further development, the net appropriation of well fields such as 10, 19, 20, and 57, which satisfy 100 percent of the net appropriation, may be increased. The limits of these increases are investigated in the next section.
In an attempt to find the maximum amount of water that can be pumped from these 61 well fields, we generated four more yearly optimal pumpage policies with 25, 20, 15, and 10 percent. In these policies the net appropriation, (k,n), as a constraint was set equal to a large enough value so that the usable saturated thickness together with continuity (equations 9-d and 9-e) controlled the maximum allowable pumpage. The pumpage policies generated under this condition are designated as optimal pumpage policies without net appropriation as a constraint. In Figures 11 and 12b the total optimal pumpage and yearly optimal pumpages are plotted as a function of γ and time. As expected, when net appropriation as a constraint is raised, more water becomes available for pumpage and pumpage will take place up to the usable saturated thickness. However, this increase is rather insignificant for small γ's. Only if a large percentage of saturated thickness is allowed to be used does the raising of the net appropriation constraint allow a noticeable increase in pumpage. Appendix C shows the spatial and time distribution of optimal pumpage policies without net appropriation as a constraint. This Appendix further supports the conclusions reached by Sophocleous (1980, 1981) that some areas of the Valley will not be able to support the present appropriation over a long period of time. Indeed for γ = 10 percent, some well fields (for example, 33, 34, 45, and 60) must be considered inoperative or at best marginal. Depending on the management district's and irrigators' points of view, several more well fields may be eliminated. This will make more water available for the adjacent well fields. Even for γ = 25 percent some of these well fields (such as well field 34) remain inoperative.
Table 1 summarizes the results obtained from the management model with and without net appropriation as a constraint. For γ = 10 percent only 2.6 percent increase in pumpage can be expected when net appropriation is removed as a constraint, while for γ = 25 percent this increase is 22.7 percent.
Table 1--Comparison of the Five-Year Optimal Pumpages With and Without Net Appropriation as a Constraint.
| Optimal Pumpage (1000 ac-ft/5 years) |
|||
|---|---|---|---|
| γ % Change |
With Net Appropriation as a Constraint |
Without Net Appropriation as a Constraint |
% |
| 10 | 96.9 | 99.4 | 2.6 |
| 15 | 135.4 | 144.5 | 6.7 |
| 20 | 167.0 | 191.9 | 14.9 |
| 25 | 191.7 | 235.2 | 22.7 |
In order to evaluate the potential of the aquifer over a longer period of time, the optimal pumpage policies were calculated on a two-year basis for a total of 10 years for γ = 25 percent of the usable saturated thickness. In these calculations, for well fields that had the potential to deliver more water than the two-year net appropriation, the upper limit of pumpage, (k,n), was raised so that all the usable saturated thickness (25 percent of 1979-80 saturated thickness) was used up. The results of these calculations (Appendix D) show that over a 10-year period a total of 323,181 acre-feet (about 50 percent of the 10-year net appropriation) may be pumped from these 61 well fields if not more than 25 percent of the saturated thickness at each well field is used. The appropriations shown in column 2 of Appendix D for well fields 5, 10, 14, 20, 22, 23, 30, 50, 51, 53, 57, and 61 may be increased to the levels shown in columns 3 through 7 if desired. Well fields 33, 34, 37, 41, and 42 must be dropped from a 10-year management plan. other well fields, such as 4, 27, 28, 43, and 45, can be considered marginal at best, and if they are dropped from a 10-year management plan more water becomes available for adjacent wells.
In this study we have developed a groundwater management model based on the use of linear systems theory and linear programming. This model is capable of calculating the best pumpage policies (optimal) subject to physical and institutional constraints. It was tested for two hypothetical aquifers and the results were validated. Then, this model was applied to the Pawnee Valley of south-central Kansas, an area for which considerable hydrogeologic data had been prepared.
The application of the management model to the Pawnee Valley was done for 61 hypothetical well fields for two time periods, five and 10 years. For the five-year time period, yearly optimal pumpage policies were generated, which allowed a certain percentage or less of the 1979-80 saturated thickness at each well field to be used up during this period. These percentages were set at y = 10, 15, 20, and 25 percent. The upper limit of pumpage was set equal to the net appropriation for that site. with these data four policies were generated and were designated as five-year optimal pumpage policies with net appropriation as a constraint. In another analysis, four more policies were generated using the same data, except it was made certain that all the usable saturated thickness was used up. This was done by raising the level of net appropriation. This policy was designated as five-year optimal pumpage policy without net appropriation as a constraint.
For the 10-year time period, two-year optimal pumpage policies were generated using 25 percent of the saturated thickness without net appropriation as a constraint. This analysis shows that for the next 10 years about 50 percent of the 1979 net appropriation may be satisfied (about 32,318 acre-feet/year).
The basic conclusion reached in this study is that the groundwater resources in the Pawnee Valley are highly over-appropriated and some action by the irrigators must be taken to slow down the rate of depletion of this resource. There seems to be little hope that the 1979 net appropriation of 64,018 acre-feet may be pumped from the aquifer, unless the irrigators and the groundwater management districts decide to use a high percentage of the saturated thickness over the next five or 10 years. At best 40,000-50,000 acre-feet/year may be pumped over a five-year period, and 30,000-35,000 acre-feet/year may be pumped over the next 10 years if 25 percent of the saturated thickness is allowed to be used up.
One may recommend that the users of this precious natural resource work together to establish procedures for monitoring water usage and levels. A management plan may be designed for a period of time, say 10 years, to reallocate the groundwater resources based on seniority, saturated thickness, and a crop-rotation plan. In such a plan, data provided in this report may become a useful guide. For example, according to Appendix D, not more than 2,751 acre-feet can be pumped from well field 1 for the next 10 years if only 25 percent of the 1979-80 saturated thickness is allowed to be used. This is 16 percent of the 1979 net appropriation to this well field. Therefore, in a management plan, only about 2,700 acre-feet of water are available for the users associated with well field 1. On the other hand, according to Appendix D, well field 57 can deliver considerably more water (49,911.0 acre-feet or 279 percent of the 1979 net appropriation) than has been appropriated. Therefore, the farmers can apply for further appropriations in this area.
The computational results in this report must be used with caution and considerable judgment. This is because of the inherent assumptions that exist in any groundwater management model and the data used in it. The data and model used in this study represent the state of the art in data collection and processing. This study demonstrates the use of modern techniques in the management of a limited resource such as groundwater in some areas of Kansas. The results can be of help to the managers of the groundwater management districts and the Chief Engineer of the Kansas Department of Agriculture, who share the responsibility of management of groundwater resources in the Pawnee Valley. Because of the errors that exist in any data collection and processing, one has to use professional judgment when using these results. Our recommendation is that these results be used as a guide rather than as an absolute.
I wish to thank Professor Thomas Maddock, III, University of Arizona, Tucson, and Dr. Steve Gorelick, U.S. Geological Survey, Menlo Park, California, for their review of the manuscript and for their comments.
Bathala, C. T., Rao, Ramachandra, and Spooner, J. A., 1977, Application of linear systems analysis to groundwater evaluation studies: Purdue University Water Resources Research Center, Technical Report 91, 128 p.
Bear, Jacob, 1979, Hydraulics of groundwater: New York, McGraw-Hill, 567 p.
Cheng, D. K., 1959, Analysis of linear systems: Reading, Mass., Addison-Wesley, 431 p.
Dreizin, Y., 1975, Applications of the superposition approach to the modeling and management of ground and surface water resources: Ph. D. Thesis, Case Western Reserve University, 293 p.
Gorelick, S. M., and Remson, I., 1982, optimal dynamic management of multiple groundwater pollutant sources: Water Resources Research, v. 18, no. 1, p. 71-76.
Hall, F., and Moench, A. F., 1972, Application of the convolution equation to stream-aquifer relationships: Water Resources Research, v. 8, no. 2, p. 487-493.
Knowles, T. R., Claborn, B. J., and Wells, D. M., 1972, A computerized process to determine aquifer characteristics: Water Resources Center 72-5, Texas Tech University, Lubbock, Texas, 103 p.
Jacob, C. V., 1944, Notes on determining permeability by pumping tests under water-table conditions: U.S. Geological Survey, Mimeograph Report, 25 p.
Maddock, T., III, 1972, Algebraic technological function from a simulated model: Water Resources Research, v. 8, no. 1, 18 p.
Maddock, T., III, 1974a, A program to compute aquifer response coefficients: U.S. Geological Survey, Open-File Report 75-612, 43 p. [available online]
Maddock, T., III, 1974b, Nonlinear technological functions for aquifers whose transmissivities vary with drawdown: Water Resources Research, v. 10, no. 4, p. 877-881.
Moench, A. F., and Kisiel, C. C., 1970, Application of the convolution relation to estimating recharge from an ephemeral stream: Water Resources Research, v. 6, no. 4. p. 1087-1094.
Morel-Seytoux, H. J., and Daly, C. J., 1975, A discrete kernel generator from stream-aquifer studies: Water Resources Research, v. 11, no. 2, p. 253-260.
Murtagh, B. A., and Saunders, M. A., 1977, MINOS: A large-scale nonlinear programming system: Stanford University Department of Operations Research Systems Optimization Laboratory Technical Report SOL 77-9, 127 p.
Sophocleous, M., 1980, Hydrogeologic investigations in the Pawnee Valley, Kansas: Kansas Geological Survey, Open-File Report 80-6, 167 p.
Sophocleous, M., 1981, The declining groundwater resources of alluvial valleys: A case study: Ground Water, v. 19, no. 2, p. 214-226.
Theis, C. V., 1935, The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using groundwater storage: Transactions of the American Geophysical Union, v. 16, p. 519-524.
Trescott, P. C., Pinder, G. F., and Larson, S. P., 1976, Finite-difference model for aquifer simulation in two dimensions with results of numerical experiment: Techniques of Water Resources Investigations of the U. S. Geological Survey, Book 7, Chapter C1, 116 p. [available online]
Venetis, C., 1971, Estimating infiltration and/or the parameters of unconfined aquifers from ground water level observations: Journal of Hydrology, v. 12, p. 161-169.
Kansas Geological Survey, Groundwater Management Options for the Pawnee Valley
Placed on web June 15, 2012; originally published in 1982.
Comments to webadmin@kgs.ku.edu
The URL for this page is http://www.kgs.ku.edu/Publications/Bulletins/GW4/index.html