Kansas Geological Survey, Bulletin 233, p. 320-334
by
Michelle A. Kominz,1 John Beavan,2 Gerard C.Bond,2 and Jerry McManus2
1University of Texas
2Lamont-Doherty Geological Observatory
Methodologies are suggested for the analysis of cyclic sediments. These include (1) linear analysis to determine whether cycles are of approximately constant duration and whether the relation between thickness and time is facies dependent and (2) multiple prolate-spheroidal windowing spectral analysis to determine whether time-series data indicate periodicities, either of the primary cycles or of higher or lower orders. The results of both methods are compared to a null hypothesis as a semiquantitative test of periodicity. Application of the methods to Newark Supergroup lacustrine cycles suggests that the primary cycles are approximately periodic and record a response to astronomical precession. The time represented by a given thickness of the different facies increases with the depositional water depth of that facies and with decreasing grain size. Precessional index cycles and long-period precessional index beats, or eccentricity, are strongly recorded in the spectra. Spectral results suggest but do not prove lengthening of the periodicities of orbital parameters since 200 Ma.
An Acrobat PDF file containing the complete paper is available (1.2 MB).
Repetitive patterns of sediment deposition have long been observed and studied. These cyclic sediments have been used as a constraint on time at least since Croll (1875) and Gilbert (1895) suggested that ancient rhythmic sediments may correspond to climatic forcing driven by periodicities of the earth's motion. Second- and third-order cycles (2-6-m.y. duration) have been used to correlate and establish relative age in stratigraphic sections by applying the methods of sequence stratigraphy [e.g., Vail et al. (1977), Haq et al. (1987), and Ross and Ross (1988)]. It is not surprising, therefore, that there has been an increasing interest in using higher-order (fifth- and sixth-order) cycles for correlation and time constraint [e.g., Fischer (1986), Goodwin and Anderson (1985), Kauffman (1988), and Ginsburg (1989)]. The suggestion that these high-frequency cycles can be used to constrain time is largely based on the possibility that they are formed in response to climatic forcing by periodic changes in the earth's orbit and the tilt of the earth's axis. If this is the case, the cycles represent predictable periods of time.
If these high-frequency cycles (10-400-k.y. duration) can be shown to be periodic (i.e., of constant durations) and if the periods can be determined, the benefits will be considerable. Dating by means of cyclic stratigraphy would help to establish the duration of stratigraphic stages and thus to determine time duration in equivalently aged noncyclic strata [e.g., Smith (1989)]. Periodic peritidal cycles can be used to estimate third-order accommodation variation by means of Fischer plots (Fischer, 1964; Read and Goldhammer, 1988; Goldhammer et al., 1990; Bond and Kominz, this volume). Rates of evolution of taxa in ancient strata can be determined. These results would improve our understanding of the planetary interactions that cause the periodic variation of cycles while increasing our understanding of the response of climate to those variations (Berger et al., 1989). Although periodicity of ancient cycles has been suggested by many researchers [e.g., Grotzinger (1986), Herbert and Fischer (1986), and Goldhammer et al. (1987)], it has proven very hard to document. For example, Algeo and Wilkinson (1988) showed that only in a few instances is periodicity of climatic origin strongly indicated by the geologic record.
In this article we develop methodologies designed to answer the question, Are ancient cyclic sediments periodic? We employ the suggestion that facies-specific accumulation rates and clearly identifiable cycles can be used to help determine whether those cycles are periodic (Kominz and Bond, 1990), and we employ improved statistical procedures. We apply linear statistical methods that allow us to use all cycles (not just those that contain all facies) and all results (not just the positive results). Multiple-window spectral analysis allows prediction of ranges of error on the power spectral density estimates. These two statistical methods are applied to two lacustrine cyclic sequences of the Newark Supergroup. To test the significance of the two statistical procedures, we develop a null model. For an example of the application of these techniques to peritidal carbonate sequences of the Middle Cambrian, refer to Bond et al. (this volume). We do not suggest that these methods will be useful for all strata or that other techniques cannot be and/or have not been used successfully [e.g., Herbert and Fischer (1986)]. This is, however, a step in our attempt to address this problem.
In working with ancient sediments (pre-Pleistocene), stratigraphers commonly estimate the time represented by the observed thickness of sediment (here termed 11 effective accumulation rate" or EAR) by interpolating between poorly constrained available dates. Thus it is commonly impossible to differentiate the EARs of different facies within a cyclic sequence. However, Recent sedimentation rates tend to be facies dependent [e.g., Kukal (1990) and Schlager (1981)], as are compaction, erosion, and other postdepositional diagenetic effects [e.g., Kukal (1990), Goldhammer et al. (1987), Chilingarian and Wolf (1975), and Bond and Kominz (1984)]. All these factors contribute to the facies' EARS.
The gamma (γ) method tests two assumptions: (1) that the EAR of each facies is approximately constant and is facies dependent and (2) that each cycle represents the same period of time (Kominz and Bond, 1990). This is done by assigning to each facies i an unknown constant γi, the time represented per unit thickness of sediment (or the inverse of the EAR) and by assigning an arbitrary constant cycle period Tcy to all cycles. The cycle period for one cycle is then equal to the sum of the γi multiplied by the thicknesses (ci) of the facies in that cycle (fig. 1). That is,
![]()
Each sediment cycle provides a linear equation with the unknowns being the γi and the knowns being the ci and Tcy. The period of the cycle is assigned based on geologic constraints or is given a value of 1 if the cycle period is unknown. Because cyclic sequences are composed of many cycles, this procedure generally yields an overconstrained problem in linear systems analysis.
Figure 1--Illustration of the assumption that each facies may have its own unique relation between time and thickness. This is compared to the usual assumption that the observed sediment thickness is proportional to age but independent of facies. The slopes, or the γi values, given here are arbitrary. Actual values of γi are calculated by applying a least-squares analysis (see text). Ti is the age of facies i since the start of that cycle; Tcy is the total time in cycle A; ti is the time represented by the ith facies; Ci is the composite thickness including facies i from the start of a cycle; ci is the thickness of facies i in a given cycle; and γi is the ratio of observed sediment thickness and the time represented by facies i.
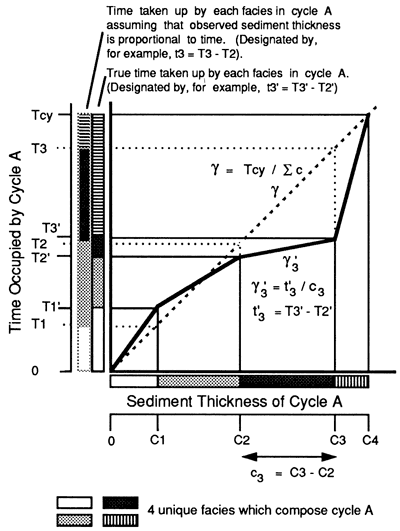
In this article we solve the linear problem using a positive least-squares inversion (Lawson and Hanson, 1974; Menke, 1989). The observed data matrix is composed of the facies thicknesses of all cycles. The method constrains the resulting predictions of γ to be nonnegative, consistent with the fact that geologically reasonable EARs cannot be negative. However, positive results are identical with those obtained by classical unconstrained least-squares inversion. Values of γ that would be negative when using the classical least-squares method are generally reduced to 0 by the positive least-squares inversion.
An indication of the validity of the estimated γ values is obtained from the following procedure. The calculated γi are used to obtain the durations of each cycle. From individual cycle durations the average cycle duration and the standard difference between calculated and predicted cycle durations are obtained. The cycle with the largest difference from Tcy is then removed, and the entire analysis is repeated using all the remaining cycles to calculate γ values. Average cycle duration and standard differences are again calculated for all cycles. If there are some cycles that are different from the rest, it is reasonable to assume that removing these cycles will cause a significant change in the calculated γ values and in the predicted cycle periods. This procedure is continued until the number of cycles remaining is equal to the number of facies present. Consistency of γ results and consistency of predicted average cycle period suggest that γ values are correct and cycle periods are constant within the uncertainty indicated by the calculated cycle durations.
If the record is continuous, spectral analysis can be used to determine whether the cycles are periodic and/or whether periodic components other than the identified cycles are present in the record. In this article we employ the multiple prolate-spheroidal window spectral technique described by Thomson (1982). The assumptions of this spectral method include the following: The data are stationary (independent of the starting time), real, ergodic (all possible values are likely to be reached in any finite time series), of zero mean, and Gaussian. This method has the following advantages: It tends not to produce peaks as a result of sampling error (bias); it increases in accuracy with increasing sample size; it yields fairly accurate results even when the data do not fully meet the assumptions of the model; and it provides statistical estimates of the error. As the number of windows used in the analysis increases, the accuracy of the magnitude of the calculated power spectral density increases and the accuracy of the frequency of peaks decreases (bandwidth increases). Here, we use four windows and report 90% confidence limits on the amplitude.
When linear analysis shows that γ values can be determined, a time scale is generated by multiplying observed thicknesses by the estimated γ values of each facies. This should provide a more accurate estimate of the duration of deposition of each sedimentation interval of a given facies. We perform the spectral analysis on two time series, one with and one without they correction, to determine what effect, if any, the corrections have on the spectral results.
Statistical testing requires comparison of observed data with a null model. This is true for both the least-squares and the spectral method. The observed sedimentary sequences are not random in their characterization because they are composed of repeating (cyclic) facies whose thickness distribution has some mean and standard deviation. We generate semirandom series with a Gaussian noise generator. Facies thickness distributions are constrained to have mean and standard deviations equivalent to those of the observed stratigraphic section. Negative facies thicknesses are set to 0, resulting in cycles containing some missing facies. No assumptions are made in this procedure about either the duration of individual cycles or the EARs of the facies.
We perform the same positive least-squares inversion and spectral analysis on the generated cyclic sequences as on the observed strata. Comparison with results from the observed section allows for a semiquantitative assessment of the assumptions of the statistical analyses.
The Newark Supergroup consists of lacustrine to fluvial sediments that were deposited in the Mesozoic rift basins that preceded continental breakup and the formation of the Atlantic ocean (Van Houten, 1964, 1969; Luttrell, 1989; Olsen et al., 1989b). Mafic lava, predominantly in the form of sills, is also common in the sequence and is important in providing age constraints. On a finer scale, abundant cyclic strata have been used to correlate basins and have been suggested as a possible tool for age control (Olsen et al., 1989b; Schlische and Olsen, 1990).
The primary cycles in the Newark Supergroup are termed Van Houten cycles (Olsen, 1984, 1986). Van Houten cycles begin at the base with exposed, generally oxidized, mud-cracked, and bioturbated lacustrine facies, possibly including intermixed fluvial facies. These shallowest facies grade upward to deeper-water, less oxygenated lacustrine sediments with fewer mudcracks and better preserved fossils, sometimes including reptile tracks. These may be overlain more abruptly by the deepest-water facies, consisting of black varved, calcareous mudstones lacking bioturbation and including well-preserved fossils. We use the depth-rank classification of facies defined by Olsen (1984, 1986); this classification system assigns ranks to the facies types ranging from 0 (shallowest) to 6 (deepest).
Within the Newark Supergroup the primary Van Houten cycles are bundled into second- and third-order cycles, that is, repetitive packages of four to five Van Houten cycles with increasing predominance of deep-water facies form second-order cycles. These, in turn, are grouped in packages of four or more increasingly deep-water sets of third-order packages. This hierarchy of cyclicity (approximately a 1:5 and a 1:20 ratio relative to the primary Van Houten cycles) is consistent with the ratios of 2 of the predicted sets of periods for the earth's orbit. Olsen (1986) and Olsen et al. (1989b) have suggested a correlation of the Van Houten cycles with orbital precession (≈ 20,000 years, the average period of the precession index; Berger, 1977) and the higher-order bundles with orbital eccentricity (period ≈ 100,000 and 400,000 years; Berger, 1977).
Olsen (1986) and Olsen et al. (1989b) provide further support for the orbital control of the cyclicity through the application of spectral analysis to depth-rank stratigraphic sections. The ages of the cyclic sequences were calibrated by both dating lavas and counting varves (assumed to be annual). A preliminary application of γ analysis to two Newark Supergroup sequences by Kominz and Bond (1990) yielded conclusions consistent with those of Olsen et al. (1989b), indicating that climatic forcing was due to orbital variation. Their analysis also indicates, however, that the EARs of the different facies vary considerably within these strata.
We do not suggest that orbital forcing of this record is in need of further testing. Rather, we accept the previous interpretations and take the average duration of a Van Houten cycle to be approximately 21,000 years, the mean period of the precessional index. As such, these strata are ideal for both γ analysis and spectral analysis and a useful test for the more sophisticated statistical methods employed here.
We use the same stratigraphic sections in this analysis as did Kominz and Bond (1990). The sections are cyclic strata of Hettangian age and are designated the East Berlin Formation (from the Hartford basin; Olsen, 1986; Olsen et a]., 1989a) and the Towaco Formation (from a drilled core in the Newark basin; Olsen, 1986) (fig. 2). These two sections were selected for use in γ analysis because of the relatively large percentage of cycles that include both shallow- and deep-water facies (11 of 21 identifiable cycles). The sections have been correlated by Olsen (personal communication, 1989) by means of the distinctive Westfield fish bed (fig. 2). As such, the time represented by corresponding cycles is likely to be approximately constant. However, because the two sections were deposited in different basins with different subsidence rates and different sediment supplies, the Towaco cycles are, on average, 2.075 times the thickness of the East Berlin cycles. For the analyses we make the assumption, as did Kominz and Bond (1990), that the ratios of γ values of the different facies are constant and that the absolute values are not. This assumption was tested by applying the positive least-squares analysis to the individual cyclic sequences and to the two sequences together.
Figure 2--Stratigraphic sections for the Towaco and East Berlin Formations. Depth-rank facies interpretations from Olsen (1986) and Olsen et al. (1989a). The cycles used in the analyses are given number-letter designations. The inset gives the approximate locations of the two sections. The fish symbol is drawn adjacent to the Westfield fish bed (depth-rank 6 facies), which has been correlated between the two basins (Olsen, personal communication, 1989).
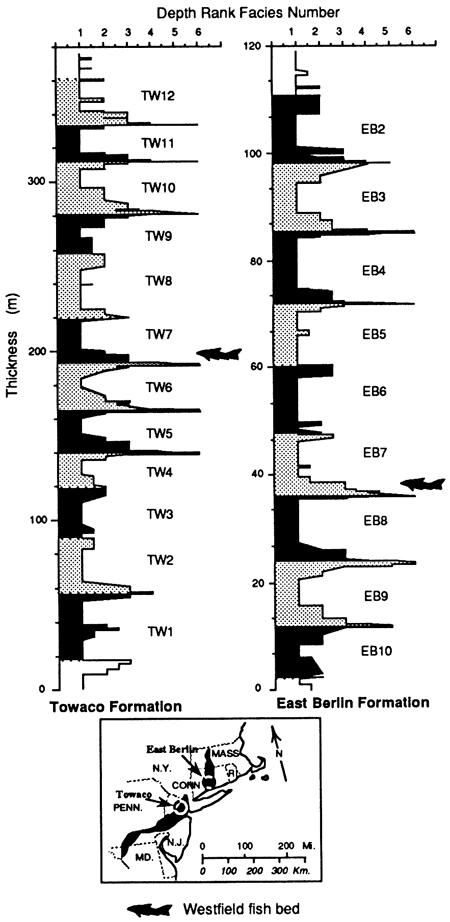
Table 1--Observed thicknesses of depth-rank facies for Towaco (TW) formation and East Berlin (EB) formation cycles (fig. 1). Source: Olsen (personal communication, 1989).
Thicknesses of East Berlin facies have been multiplied by 2.075.
The two sets of cycles were used independently in positive least-squares analyses to estimate γ values for each formation (table 2, fig. 2). The entire data set was used as the input for the combined positive least-squares analysis (table 2, fig. 3).
| Cycle | Thickness (m) of Depth-Rank Facies | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5/6 | |
| TW12 | 15.85 | 5.30 | 5.40 | 0.80 | 0 |
| TW11 | 15.20 | 3.20 | 2.95 | 0.60 | 0.65 |
| TW10 | 10.50 | 13.84 | 4.01 | 0.94 | 1.10 |
| TW9 | 11.65 | 9.35 | 0.81 | 0.89 | 0.61 |
| TW8 | 23.26 | 14.33 | 0 | 0 | 0 |
| TW7 | 18.55 | 2.80 | 5.16 | 1.19 | 0.01 |
| TW6 | 10.30 | 8.86 | 6.63 | 0.40 | 1.01 |
| TW5 | 12.60 | 5.10 | 6.00 | 0.99 | 0.91 |
| TW4 | 12.50 | 6.00 | 0.80 | 0 | 0.70 |
| TW3 | 19.90 | 10.10 | 0 | 0 | 0 |
| TW2 | 25.75 | 3.25 | 2.50 | 0 | 0 |
| TW1 | 28.78 | 7.26 | 3.75 | 1.0 | 0 |
| EB2 | 12.74 | 8.90 | 3.88 | 0.62 | 0 |
| EB3 | 11.10 | 11.90 | 1.61 | 1.18 | 0.91 |
| EB4 | 20.29 | 3.57 | 2.78 | 0.41 | 0.42 |
| EB5 | 19.99 | 2.77 | 0.56 | 0 | 0.64 |
| EB6 | 19.84 | 4.99 | 2.29 | 0 | 0 |
| EB7 | 15.83 | 1.91 | 3.65 | 0.89 | 0.71 |
| EB8 | 17.35 | 2.68 | 4.32 | 0.73 | 1.04 |
| EB9 | 10.40 | 8.24 | 2.30 | 0.44 | 1.64 |
| EB11 | 6.57 | 12.96 | 0.02 | 0.08 | 0.91 |
The cycles used in the γ analysis are identified in fig. 2, and facies thicknesses are given in table 1. In all cases (except fig. 2) the East Berlin cycles were normalized to the average thickness of the Towaco cycles. Depth-rank facies 5 and 6 are combined into a single facies for the γ analysis because they are rare in the outcrops and are similar in character. The constrained least-squares γ analysis was run for each of the sections separately and for the two sections combined. The cycle period (Tcy) was set at 21,000 years, the average precessional period at present (Berger, 1977). The results of these analyses are plotted in fig. 3 and presented in table 2. The most consistent results are obtained from the combination of the two data sets. We first consider the results of the individual sequence calculations.
The results from the East Berlin section alone fail to estimate γ values (fig. 3, top). In no case was a solution obtained for they value of depth-rank facies 4, and a solution was obtained for four of five γ values only by the first two calculations. These 2 analyses estimated γ value ranges of 0.4-0.95 k.y./m for the shallowest facies (1 through 3). The γ estimates for depth-rank facies 5/6 are considerably higher (≈ 2.5 k.y./m).
Figure 3--(Left) Positive least-squares results from analyses of the East Berlin Formation cycles alone, the Towaco Formation cycles alone, and the two sections combined. (Right) Average durations of all cycles and standard error for all cycles.
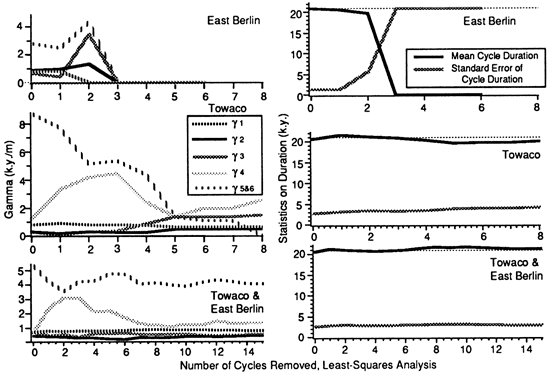
Table 2--Positive least-squares γ results. The results from three analyses are presented here. Each section was analyzed independently and the two sections were combined to yield the final set of results. For 17 cycles removed in the combined data, 4 cycles were used to generate 5 unknowns, resulting in large uncertainties in the results. Input data given in table 1.
| Number of Cycles Removed |
γ Values (k.y./m) for Depth Rank | Duration Error Analysis (k.y.) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Standard Difference | Average Period | ||||||||
| 1 | 2 | 3 | 4 | 5/6 | Cyc-Used | All-Cyc | Cyc-Used | All-Cyc | |
| East Berlin | |||||||||
| 0 | 0.786 | 0.884 | 0.655 | 0.000 | 2.803 | 1.338 | 1.338 | 20.915 | 20.915 |
| 1 | 0.792 | 0.948 | 0.405 | 0.000 | 2.459 | 0.970 | 1.466 | 20.955 | 20.578 |
| 2 | 0.000 | 1.326 | 3.445 | 0.000 | 4.304 | 6.218 | 5.743 | 19.159 | 19.722 |
| 3 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 21.000 | 21.000 | 0.000 | 0.000 |
| 4 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 21.000 | 21.000 | 0.000 | 0.000 |
| 5 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 21.000 | 21.000 | 0.000 | 0.000 |
| 6 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 21.000 | 21.000 | 0.000 | 0.000 |
| Towaco | |||||||||
| 0 | 0.789 | 0.252 | 0.287 | 1.250 | 8.735 | 2.887 | 2.887 | 20.603 | 20.603 |
| 1 | 0.880 | 0.168 | 0.070 | 3.298 | 7.714 | 2.054 | 3.284 | 20.799 | 21.575 |
| 2 | 0.798 | 0.288 | 0.303 | 4.160 | 5.128 | 1.645 | 3.469 | 20.871 | 21.216 |
| 3 | 0.775 | 0.239 | 0.361 | 4.465 | 5.348 | 1.493 | 3.449 | 20.894 | 20.907 |
| 4 | 0.745 | 0.241 | 0.851 | 2.382 | 4.345 | 1.111 | 3.511 | 20.941 | 20.371 |
| 5 | 0.625 | 0.455 | 1.347 | 1.313 | 1.324 | 0.242 | 4.006 | 20.997 | 19.614 |
| 6 | 0.632 | 0.439 | 1.317 | 1.924 | 1.084 | 0.000 | 4.076 | 21.000 | 19.779 |
| 7 | 0.632 | 0.439 | 1.317 | 1.924 | 1.084 | 0.000 | 4.076 | 21.000 | 19.779 |
| 8 | 0.617 | 0.463 | 1.439 | 2.481 | 0.000 | 0.000 | 4.379 | 21.000 | 19.957 |
| East Berlin + Towaco | |||||||||
| 0 | 0.728 | 0.481 | 0.722 | 0.720 | 5.362 | 2.746 | 2.746 | 20.641 | 20.641 |
| 1 | 0.794 | 0.433 | 0.546 | 2.407 | 4.276 | 2.126 | 2.960 | 20.785 | 21.268 |
| 2 | 0.777 | 0.420 | 0.580 | 3.158 | 3.583 | 1.774 | 3.045 | 20.850 | 21.063 |
| 3 | 0.796 | 0.352 | 0.447 | 3.136 | 4.289 | 1.608 | 2.980 | 20.877 | 20.879 |
| 4 | 0.792 | 0.331 | 0.630 | 2.179 | 4.302 | 1.465 | 2.936 | 20.898 | 20.687 |
| 5 | 0.810 | 0.276 | 0.619 | 2.230 | 4.796 | 1.344 | 2.969 | 20.914 | 20.861 |
| 6 | 0.847 | 0.241 | 0.666 | 1.714 | 4.755 | 1.184 | 3.081 | 20.933 | 21.081 |
| 7 | 0.865 | 0.367 | 0.597 | 1.312 | 4.094 | 0.886 | 3.167 | 20.963 | 21.458 |
| 8 | 0.891 | 0.339 | 0.583 | 1.242 | 4.184 | 0.730 | 3.288 | 20.975 | 21.658 |
| 9 | 0.878 | 0.367 | 0.600 | 1.152 | 4.012 | 0.654 | 3.238 | 20.980 | 21.549 |
| 10 | 0.854 | 0.440 | 0.606 | 1.264 | 3.928 | 0.481 | 3.204 | 20.989 | 21.690 |
| 11 | 0.856 | 0.424 | 0.545 | 1.238 | 4.229 | 0.374 | 3.139 | 20.993 | 21.568 |
| 12 | 0.842 | 0.417 | 0.510 | 1.506 | 4.393 | 0.269 | 3.050 | 20.997 | 21.417 |
| 13 | 0.830 | 0.454 | 0.529 | 1.315 | 4.240 | 0.103 | 3.023 | 20.999 | 21.339 |
| 14 | 0.812 | 0.482 | 0.553 | 1.385 | 4.079 | 0.045 | 2.986 | 21.000 | 21.248 |
| 15 | 0.813 | 0.477 | 0.557 | 1.399 | 4.101 | 0.000 | 2.988 | 21.000 | 21.270 |
| 16 | 0.817 | 0.468 | 0.552 | 1.399 | 4.161 | 0.029 | 2.993 | 21.003 | 21.291 |
| 17 | 0.412 | 1.268 | 0.833 | 0.000 | 0.000 | 0.000 | 5.341 | 21.000 | 17.835 |
| Averages (Kominz and Bond, 1990) | |||||||||
| 0 | 0.611 | 0.626 | 0.693 | 3.898 | 3.406 | ||||
The least-squares results are more stable for the Towaco section than for the East Berlin section (fig. 3, middle) The results show considerable variability as cycles are removed, however. As an example, there is a drop in the average cycle period and a change in the relative values of γ for all facies after removal of the fifth cycle. The earlier results (0 to 4 cycles removed) indicate that the deep-water facies (facies 4 and 5/6) have much larger γ values than the shallower facies (depth-rank 1, 2, and 3). Although these results are tenuous, the γ results are similar in character to those from the East Berlin section, suggesting that combining the two data sets is not unreasonable.
The least-squares results for the two cyclic sections together appears to be stable (fig. 3, bottom). For example, γ values estimated for the shallower water facies remain approximately constant, maintaining the same relationship to each other as more and more cycles are removed from the analysis. Estimates of γ for the deeper-water facies also maintain consistent relationships with each other and with the shallow-water sediments. There is some variation in the γ values calculated for the two deepest facies, particularly when the first two cycles are removed.
The error analysis is also useful in determining stability of least-squares results (fig. 3). The average duration of all 21 cycles fluctuates closely about the assumed cycle period, whereas the mean error remains low and relatively constant. These statistics suggest that the system is stable, implying that the two hypotheses of γ analysis may be correct, that is, that the cycle durations are essentially constant and that the EARs are approximately constant for each facies. This result seems remarkable, considering the less consistent least-squares results of the individual sections. A possible explanation may be that stable γ values are more likely when relatively large differences in facies thicknesses are present.
This explanation is supported by the results of a simple modeling experiment in which two sequences of periodic cycles were generated and analyzed (fig. 4). Facies and cycle thicknesses were derived from a combination of specified γ values, specified constant cycle periods, and random noise. The two facies were given a fast and a slow EAR. One set of cycles was generated with similar amounts of time for the deposition of the two facies. The resulting sedimentary section contains thick cycles. A second set of cycles was generated allowing more time for the deposition of the slower accumulating facies. The resulting section contains a record of thinner cycles. Both sequences were examined using the positive least-squares inversion method. Individually, each section yields an output of fluctuating (e.g., data set 1, analyses 1 and 2) or zero-valued γ estimates (e.g. data set 2, facies 1; fig 4). Because the assumption of constant γ values and cycle period are true for this model, the effect of these parameters on measured thicknesses must be obscured by the random noise. When the two sequences are combined, γ analysis yields results that are accurate and stable, despite the presence of the noise component. This supports the suggestion from the Towaco and East Berlin results that, given similar facies patterns from cycle to cycle, small variations in period or EAR or small measurement errors can result in unstable γ estimates.
Figure 4--Positive least- squares results for runs of two generated cyclic data sets and the two data sets combined. As with the East Berlin and Towaco results (fig. 3), the combined results are considerably more stable than either cyclic section alone.
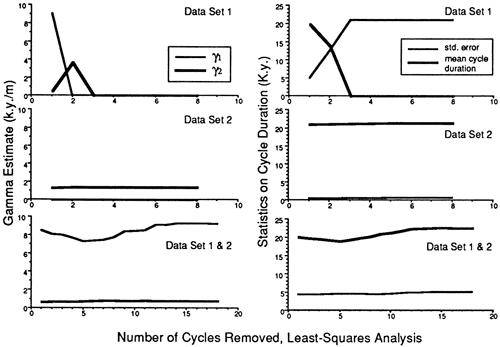
Although individual section results show poor stability, the trends are consistent with those obtained from the combined data set. This observation combined with the stability of the combined result suggests strongly that the assumption that γ values are consistent for each facies in the two sections is reasonable. Also, it suggests that γ values are applicable for the two sections even though the absolute accumulation rates differ by a ratio of 2.075.
The γ values estimated for the combined Towaco and East Berlin sections by the least-squares method are consistent with the results obtained by Kominz and Bond (1990). The highest γ values correspond to the deepest-water facies, indicating that these fine-grained sediments may have accumulated at relatively low rates and may have been subject to considerable postdepositional compaction. Although positive least-squares results consistently show a higher γ value for depth-rank facies 1 than for depth-rank facies 2 and 3, the difference is too small to be conclusive. A larger data set might resolve this difference.
Values of γ for the five facies are taken from the positive least-squares analysis after removal of eight cycles (table 2). Although the selection is somewhat arbitrary, our choice was based on the observation that fluctuations in estimates for the least stable facies, γ4, became stable at this point. The values are: depth-rank 1, γ ≈ 0.89 k.y./m; depth-rank 2, γ ≈ 0.34 k.y./m; depth-rank 3, γ ≈ 0.58 k.y./m; depth-rank 4, γ ≈ 1.2 k.y./m; depth-rank 5/6, γ ≈ 4.2 k.y./m. These values are those used to provide a time scale for spectral analysis later in this article.
Ten semirandom 25-cycle sequences were generated for comparison with the least-squares results. The distribution of thicknesses of each facies in each cycle for all 10 Gaussian random normal experiments are compared with the observed facies thickness distributions in fig. 5. For each facies the distribution of the thickness data is shown by division into 10 equal-width bins. Note that the thickness axis is the same when comparing the random data with the observed data but is unique for each facies. We wish to consider the general pattern of the distribution of each facies. In detail, the two data sets are not identical. In general, the distribution of thicknesses is broader for the Gaussian data than for the observed thicknesses so that the bins are wider. The random numbers are much more Gaussian in their distribution, with clear mean values and reduction of probability away from the mean. The modes of the two data sets rarely coincide but are not greatly different. However, the distributions are of similar magnitude with zero-thickness facies appearing at about the expected rate. Thus, in general, the overall distribution of the random data is similar to that of the observed strata.
Figure 5--Distribution of facies thicknesses. In the observed cycles there were 21 measured thicknesses for each facies. The distribution of each set of observed facies thicknesses is plotted in the histograms on the right, with thicknesses broken into 10 groups. Ten Gaussian random data sets were created using the means and standard deviations of the facies thicknesses of the observed cycles. The distribution of facies from all 10 synthetic cycles combined is shown in the histograms on the left.
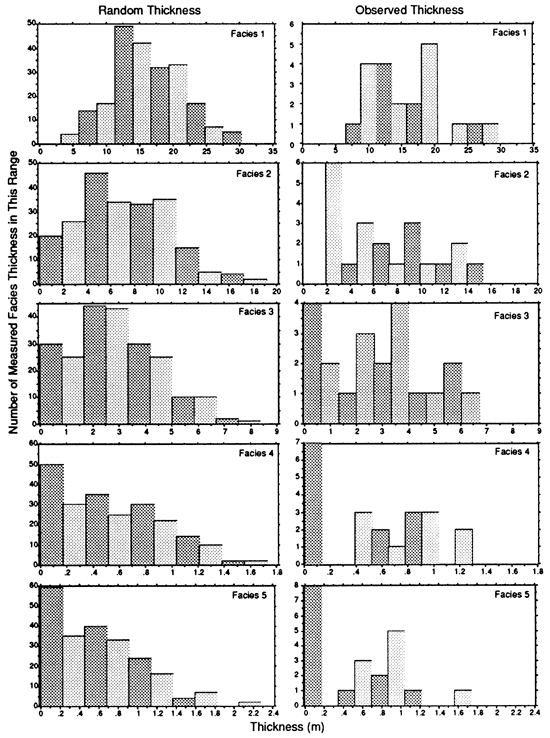
The positive least-squares method was applied to all 10 Gaussian data sets (fig. 6). Several unexpected results are apparent. Because the facies thicknesses were generated semirandomly with no regard to a constant relation between thickness and time or to the duration of each cycle, the expected result is highly fluctuating positive results mixed with zero results at best and all zero values at worst. In many cases, however, these semirandomly generated data sets do yield positive γ results. Less surprisingly, in 5 of the 10 data sets (sets 1, 3, 6, 9, and 10), 1 or more of the facies were dominated by zero-valued γ's. Also, in those sections that generate positive results, the γ values estimated as cycles are removed fluctuate more than the γ values estimated from the observed data and do not maintain consistent relations between facies. Finally, it is important to note that the average thicknesses of the facies influence but do not fully control the relative γ values assigned to that facies. That is, although all 11 sequences (random and observed) have approximately the same distribution of facies thicknesses (fig. 5), the average γ values predicted by the positive least-squares procedure vary considerably. For example, the thinner facies tend to have the higher γ values, but there are 2 random data sets (4 and 10) that produce lower γ values for facies 5 (the thinnest facies) than for facies 1 and 3 (consistently thicker facies).
Figure 6-Gamma values calculated by the positive least-squares method for the 10 Gaussian-generated data sets are plotted on the left. Corresponding cycle duration statistics are plotted on the right. Statistics from the combined Towaco and East Berlin cycles are plotted as fine lines for ease of comparison. The Towaco and East Berlin results are plotted on the same scale as an inset with result 9 for comparison. Reducing the number of cycles in the semirandom data to the number of the observed cycles does not change the pattern of the statistics.
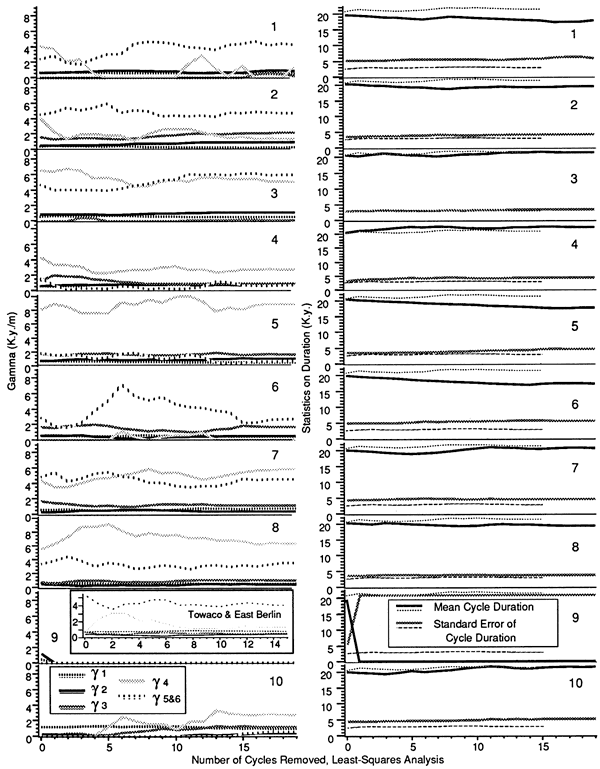
The relatively lower stability of the null model cycles is also indicated by the statistics calculated in the least-squares analysis (compare figs. 3 and 6). The standard error estimated for the observed sections is less than that for all semirandomly generated data sets except for set 3. Also, except for set 3, the average duration of the cycles predicted by the observed data is considerably more constant and remains closer to the predicted value of 21 relative to all other data sets.
The results of the γ analyses have a number of implications. First, from the semirandom data results it is clear that positive γ results alone are not sufficient to imply that the two assumptions of the γ method (constant period and constant EARs) are true. Second, although the relative thickness of each facies does exert some control on the γ values obtained, in detail average facies thickness alone does not fix γ values. As regards the Towaco and East Berlin cycles, we suggest that the γ results are different from and more stable than the semirandom series. This suggests that observed cycles are more consistent with the γ assumptions than the null model, suggesting that the two assumptions of the γ method hold for the two sections. Thus the γ values produced can be used to approximate EARs for the Towaco Formation. That is, EARs were 0.22 m/k.y. (0.72 ft/k.y.) for the deepest facies, 0.67 m/k.y. (2.2 ft/k.y.) for depth-rank facies 4, 1.7 m/k.y. (5.6 ft/k.y.) for depth-rank facies 3, 2.7 m/k.y. (8.9 ft/k.y.) for depth-rank facies 2, 1.2 m/k.y. (3.9 ft/k.y.) for depth-rank facies 1. Finally, the results also suggest that the cycles are periodic, the second assumption of γ analysis.
The γ analysis indicates that the Van Houten cycles are approximately periodic and that there is an approximately constant relation between EAR and time that is facies dependent. Here we apply another test for periodicity, spectral analysis. Because the record is continuous, it is possible to test for periodicity not only of the Van Houten cycles but also of higher-order cyclicity reported in these strata [e.g., Olsen et al. (1989b)].
We performed spectral analysis on two time series, one with and one without γ corrections for time control. Before spectral analysis, we combined the East Berlin and Towaco sections to create a composite stratigraphic section [e.g., Kominz and Bond (1990)]. The observed sediment thicknesses were multiplied by appropriate γ values (see preceding discussion and table 2) to obtain the duration of each facies in each cycle, and ages from 0 at the base were defined by the cumulative durations. The total time represented by the composite section, calculated in this manner, was 510 k.y. That value divided by the thickness of the composite section is the average time per meter thickness of the entire sequence, independent of facies. This value was used to assign ages to the section, assuming that time is proportional to thickness. The power spectral density was calculated using the spheroidal multiple-window method of Thomson (1982) with a program provided by Chave (personal communication, 1990). We compare the spectra of the two time series (time proportional to thickness and γ-corrected time) to assess the sensitivity of spectral analysis to the γ corrections.
To determine whether spectral results are meaningful, we compared them to the null model cyclic sequences described in fig. 5. To do so, we constructed time series from the Gaussian-generated facies thickness data sets. The randomly derived facies thicknesses were distributed in a cyclic pattern similar to that of the observed sections. Van Houten cycles are generally gradational, progressing from shallowest to deepest facies and then to shallowest facies again (see fig. 2). With this in mind, the semirandom cycles were distributed such that all of facies 5 was placed at the top of a cycle, followed by half of facies 4, half of facies 3, half of facies 2, all of facies 1, half of facies 2, half of facies 3, and half of facies 4. The resulting cycles are somewhat more symmetric than the observed cycles. Figure 7 shows the composite and semirandom cyclic sequences used in the spectral analysis. These sequences have been sampled at a 1-k.y. sample interval from 0 to 500 k.y., and a linear trend has been removed from the amplitude (the depth ranks are distributed about 0 rather than ranging from 1 to 5). There is no γ-corrected time series for the ninth random data set because in this case no positive γ values were obtained.
Figure 7--Time series of observed cycles (bold lines) and semirandom cycles (thin lines, with zero line equivalent to spectral pattern in fig. 8). These time series are those used in the spectral analysis. They have been sampled at a constant 1-k.y. time interval, and any linear trend has been removed. The plots at the top show the data as observed in the field and/or as generated by the Gaussian noise generator and distributed in a cyclic pattern. Each time series in the bottom set has been subjected to a complete positive least-squares analysis (fig. 6), and stable γ values have been chosen to produce the time series. In some cases only a few data points produced positive γ values for all 5 facies (e.g. data sets 1 and 10, fig. 6) and these values were used in the calculations. In one case (data set 9, fig. 6) no positive values for all 5 γ's were produced and a γ corrected time scale was impossible.
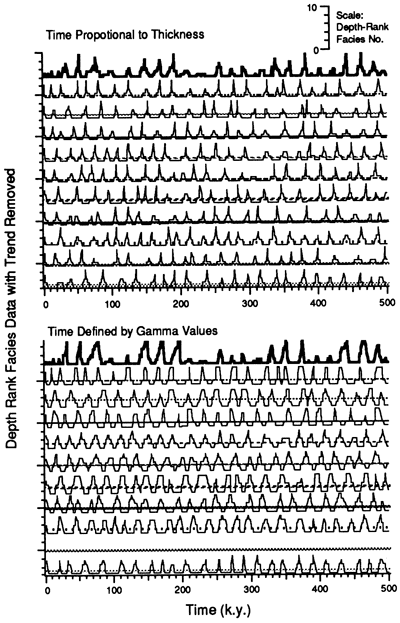
As can be seen in fig. 7, the character of the semirandom cycles is not entirely different from that of the observed composite sequence. In fact, the random sequences look highly cyclic, and the cycles could be easily picked out of the data sets. The main difference between these sequences and the observed composite sequence is the lack of the second-order grouping of the high-amplitude cycles seen in the observed data.
Given the visual evidence of cyclicity of the randomly generated sequences, it is not unexpected that spectral analysis shows these data to be periodic (fig. 8). Spectral analysis of the series with time proportional to thickness shows strong spectral peaks with maximum power between 25 k.y. and 18 k.y. and with secondary peaks ranging down to 12 k.y. There is little power at the longer periods. The average of the 10 spectra shows a broad peak running from approximately 40 k.y. to approximately 16 k.y., with power trailing off to 11 k.y. The peak reaches a maximum at ≈22 k.y. The γ-corrected random series, with an assumed period of 21 k.y. (= Tcy), show a much tighter grouping of the spectral peaks. In this case the peaks range from 25 k.y. to 20 k.y., and some secondary peaks are present at longer periods. Again, the average of the 9 spectral results centers at 22 k.y., but the peak is much tighter, ranging between 27 k.y. and 18 k.y. As noted by Kominz and Bond (1990), the magnitude of the power is higher for the γ-corrected data because with the correction more time is assigned to the higher-ranked facies.
Figure 8--Multitapered four-window spectra of the semirandom data sets shown in fig. 7. Line patterns are those of the zero lines in fig. 7. The very bold lines in these plots are the means of the data set 10 and 9 individual spectral results, respectively. See text for discussion.
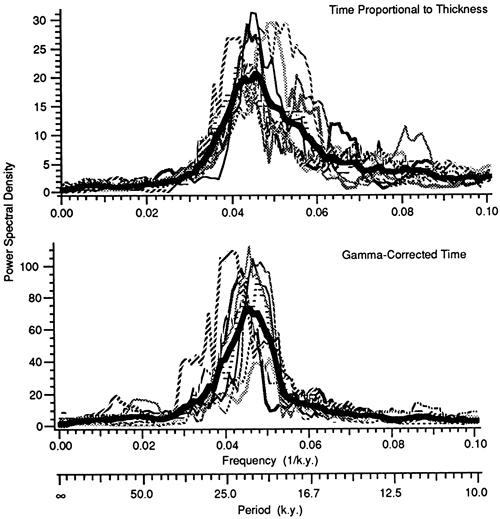
The average spectra of the random time series are compared to the spectral results for the composite East Berlin and Towaco sections in fig. 9. We show both the power spectral densities obtained for the composite section with corrected γ's and with the uncorrected time scales. Both time series produce a broad, strong peak centered at the precessional periods and a broad but lower amplitude peak at longer periods. The uncorrected section yields a broad spectral peak with a mean at 21 k.y. that encompasses both the 19- and 23-k.y. periods of the modern precession index. The strongest peak in the γ-corrected spectral result is centered at 23 k.y. Smaller peaks are somewhat separated from the main peak and are centered around 30 k.y. and 19 k.y. The long-period peak is strongly enhanced relative to the precessional peak after the γ corrections. This peak ranges from 63 k.y. to 500 k.y. for both time scales.
Figure 9--Multitapered four-window spectra of the composite East Berlin and Towaco data sets shown in bold in fig. 7. The spectra (bold line) and the lower 90% confidence limits (thin solid line) are plotted. These are compared to the mean spectra of the semirandom data sets (dashed line) from fig. 8. Apparently significant peaks are noted by horizontal bars above them, and their periodicity is given. The 19-k.y. peak is also shown in the same way in the lower graph. The line spectra predicted from orbital variations of obliquity, precession index, and precessional combination tones (table 3) are indicated on the graphs. Those above the abscissa are modern values. Those below the abscissa are those predicted for 200 Ma corrected for an assumed precessional cycle period of ≈21 k.y. See text for discussion.
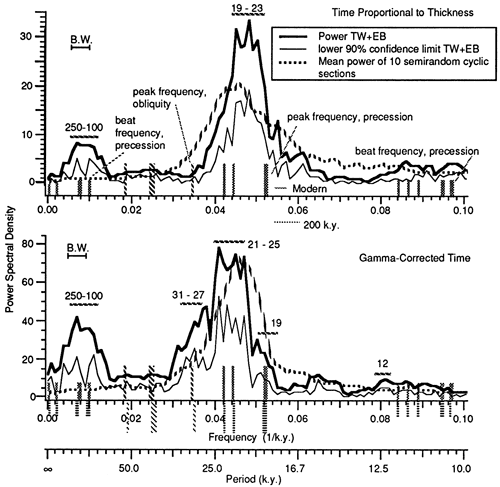
An estimate of the significance of the spectral peaks is made by comparison with the spectra of the mean semirandom data sets (see fig. 9 and table 3). A spectral peak can be considered significant if it falls within the bandwidth accuracy of the method and if the corresponding lower 90% confidence limit is above the mean value predicted from the randomly generated data. These criteria are met in the spectrum of the time scale without γ correction by a broad peak that encompasses the 100-250-k.y. period and by the main spectral peak that centers on the 21-k.y. period. The γ-corrected time series also yields significant spectral peaks in the 20-25-k.y. range and in the 100-250-k.y. range. There is also a smaller but apparently significant peak with a period of 28 k.y. A much weaker peak at 12 k.y. may also be significant.
Table 3--Periodicities of observed spectral peaks for which the lower 90% confidence limit was greater than the average spectra of the null hypothesis runs (fig. 9) compared to predicted periodicities of the earth's orbit and tilt, both modern (Berger, 1977) and at 200 Ma (Berger et al., 1990).The 200-Ma values have been multiplied by 21/19.75, the ratio of the period assumed for precession and that predicted for 200 Ma. The orbital periods are given in fig. 9 as bars. Significant spectral peaks are given at the right.
| Modern | Modified 200 Ma | Observed Spectra | ||
|---|---|---|---|---|
| γ Time | Time Proportional to Thickness |
|||
| Precession beat (destructive interference) |
2,030 | 2,159 | ||
| 413 | 439 | |||
| 131 | 140 | 250-100 | 250-100 | |
| 123 | 131 | |||
| 100 | 106 | |||
| 95 | 101 | |||
| Obliquity | 53.6 | 52.1 | ||
| 41.0 | 39.8 | |||
| 40.5 | 39.4 | 31-27 | ||
| 39.7 | 38.6 | |||
| 28.9 | 28.1 | |||
| Precession | 23.7 | 23.5 | ||
| 22.4 | 22.3 | 20-25 | 19-23 | |
| 19.2 | 19.3 | |||
| 19.0 | 19.1 | |||
| Precession beat (constructive interference) |
11.9 | |||
| 11.9 | ||||
| 11.5 | ||||
| 11.5 | ||||
| 11.2 | ||||
| 11.2 | ||||
| 10.6 | 12 | |||
| 10.6 | ||||
| 10.5 | ||||
| 10.5 | ||||
| 10.3 | ||||
| 10.3 | ||||
| 9.6 | ||||
| 9.6 | ||||
| 9.5 | ||||
The major differences between the γ-corrected and the uncorrected spectral results are (1) the exact period of the precessional peak that is significantly different from the semirandom results is higher after γ correction, (2) the long-period peaks are strengthened by γ corrections, and (3) a few additional peaks of lesser significance appeared after γ corrections were made.
It is not possible to infer details from the periods that appear to be significant within the broad precessional peak of the spectra of both time series. That the semirandom cycles are quasi-periodic is clear from their spectra (fig. 9), and this probably is controlled by the thick depth-rank facies 1 that separates the deeper facies of all cycles (see figs. 5 and 7). Because the generated semirandom cycles were actually more symmetric than the observed cycles, it is likely that these spectral peaks are exaggerated relative to a more realistic background experiment. Thus it is unreasonable to conclude that all the power in the spectrum of the observed data at these periods is insignificant, and we do not infer that the Van Houten cycles are not periodic. It is interesting that most of the power is centered on the long-period (≈ 23-k.y.) cycles after γ corrections and that a distinct peak is present, although not significant, at 19 k.y. We conclude that the Van Houten cycles are periodic, but we are unable to draw detailed conclusions of the exact periods represented within this portion of the spectra.
The longer-period and shorter-period spectral peaks appear significant relative to the spectrum of the null model because the null model has low power at these periods. Modern periods of the main terms in the series expansion of the precessional index are 23.716, 22.428, 18.976, and 19.155 k.y.; and the periods of the main terms in the series expansion of obliquity are 41.000, 39.730, 53.625, 40.521, and 28.910 k.y. [table 3; periods from Berger (1977)]. If the climatic response to the effect of precession on the insolation is nonlinear, then beat frequencies resulting from combinations of these periods will be seen in the preserved record. In the Newark Supergroup the primary cyclicity has consistently been found to be that of precession (Olsen et al., 1989b; Kominz and Bond, 1990); thus we consider here only the periodicities resulting from combination tones of the four main precessional periods. These beat periods are 413, 94.9, 99.6, 123.3, 131.3, and 2,030 k.y. when the beats interfere destructively (frequencies subtracted). These are also the periods of eccentricity from Berger (1977). The precession beat periods are 11.5, 10.5, 10.6, 10.3, 10.3, and 9.5 k.y. when the beats interfere constructively (frequencies added), and 11.9, 11.2, 9.5, and 9.6 k.y. for half-period multiples of the primary periodicities. Although this seems like a large number of periods, many are nearly identical and would not be distinguishable in the stratigraphic record.
Astronomical calculations by Berger et al. (1989a, b) suggest that the average periods of precession and obliquity were probably shorter in the past than they are today, mainly because of systematic lengthening of the earth-moon distance with time. Berger et al.'s model estimates the main periodic components of precession to have been 18 k.y. and 21.5 k.y. at 200 Ma (Hettangian time), compared to the modern values of 19 k.y. and 23 k.y. The main obliquity terms of 41 k.y. and 53 k.y. were 37 k.y. and 47 k.y. at 200 Ma. The precessional destructive interference beats are not changed, however, because the ratios of the four main frequencies of precession remain the same (Berger, personal communication, 1990). For the power spectra shown in fig. 9, we used the average of the modern 19-k.y. and 23-k.y. precession signals, 21 k.y., for the cycle period in our γ analysis and thus to establish a time scale. If the actual mean cycle duration is 19.75 (the average of the two 200-Ma precessional peaks), then the values of the orbital peaks are those predicted for 200 Ma but scaled to a precessional peak of 21 k.y. These are: precession, 19 and 23 k.y.; obliquity, 28, 39, and 52 k.y.; precessional beats, 439, 101, 106, 131, 140, and 2,160 k.y. and 11.8, 11.5, 11.3, 10.5, 10.3, and 9.6 k.y. The modern and the scaled 200-k.y. obliquity, precession, and precessional beat frequencies are plotted along with the spectra in fig. 9 and are given in table 3.
Many of the observed spectral peaks are present in the orbital periodicities, particularly for the scaled 200-Ma estimates. The 100-142-k.y. peak is particularly well defined after γ corrections in the power spectral density and appears to divide into 2 peaks by the lower 90% confidence interval. This peak is particularly well associated with the 101-140k.y. peaks predicted as a combination tone of precessional periods at 200 Ma. The resolution is not sufficient, however, to distinguish the 200-Ma periodicity from the modern periodicity predicted for orbital variations. Longer-period peaks are poorly defined and beyond the resolution of the data.
The spectral density peak calculated from the y-corrected time scale and centered at 28 k.y. appears to be significant relative to the semirandom experiment. This peak corresponds with one of the obliquity periods for the 200-Ma model. Because this is not a prominent peak in the obliquity signal, it might not be expected to be present in the absence of a strong 39-k.y. peak. The results are suggestive of the presence of a weak obliquity signal in the Towaco and East Berlin sections.
Spectral peaks at lower periodicities are poorly defined. Only the peak at 12 k.y. after γ corrections is significant. This spectral peak could represent combination tones of precession assuming either the 200-Ma or the modern orbital model. Analysis of a larger data set would be needed to test the significance of high-frequency components of the record.
The analysis of cyclic sequences for which facies thicknesses were generated according to a Gaussian normal random distribution demonstrates that positive γ results alone are not sufficient to imply that cycles are periodic. That is, least-squares analysis of semirandom facies data produced by a Gaussian noise generator did occasionally yield nonnegative γ results. This emphasizes the need to compare results from real sections with an appropriate null model before drawing conclusions about the periodicity or accumulation rates of facies. The spectral density of the Gaussian-generated null model cyclic sections showed the presence of periodic components. This also emphasizes the need to compare results obtained on cyclic sequences with appropriate semirandom data before drawing conclusions regarding the periodicity of those cycles.
The results of γ analysis of the Towaco and East Berlin cycles compared with 10 semirandom cyclic sequences suggest that we can place some confidence in the assumptions of γ analysis. That is, each of the 5 facies identified has an approximately constant EAR and the durations of the 21 cycles are not random and thus could be constant. Results show that the EARs generally decrease with increasing depth of deposition and decreasing grain size of the facies.
Both the observed Towaco and East Berlin sections and generated nonrandom sections indicate that γ analysis is most likely to be successful when there are thickness variations in the facies distributions within cycles. Random errors or small differences in EARs for highly uniform cycles result in highly variable γ estimates.
Comparison of the spectra of the composite time series with the spectra of the randomly generated cyclic sequences suggests that the periodicity of the Van Houten cycles records a precessional effect on climate. Precessional destructive combination tones (or eccentricity cycles) are clearly present in the spectra. There is also a suggestion of weak spectral peaks at one of the periods predicted for obliquity. These relations are enhanced when the corrections of Berger et al. (1989a, b) for the effect of changes in the earth-moon system are considered, thus providing support for their model. These conclusions are best observed when the time scale is tuned using facies-dependent γ corrections.
Spectral analysis of the East Berlin and Towaco time series supports the suggestion that these lacustrine sediments accumulated in response to climatic forcing. Because this research has been carried out on only two sections, we can only be cautious in inferring sedimentation rates and periodicities present in these cyclic strata. However, the results are encouraging and suggest that application of this kind of analysis to a longer, equally complete record could result in a clear definition of accumulation rates of the strata involved and well-defined periodicities of the cycles.
Acknowledgment is made to the Donors of the Petroleum Research Fund, administered by the American Chemical Society under grant ACS-PRF20852-AC8, which provided the support for this research. We thank Cliff Frohlich for discussions and D. G. Smith, Daniel Tetzalaff, and Al Fischer for critical reviews. This paper is Lamont-Doherty Geological Observatory contribution 4798.
Algeo, T. J., and Wilkinson, B. H., 1988, Periodicity of mesoscale Phanerozoic sedimentary cycles and the role of Milankovitch orbital modulation: Journal of Geology, v. 96, p. 313-322
Berger, A., 1977, Support for the astronomical theory of climatic change: Nature, v. 269, p. 44-45
Berger, A., Loutre, M. F., and DeHant, V., 1989a, Astronomical frequencies for pre-Quaternary palaeoclimate studies: Terra Nova, v. 1, p. 474-479
Berger, A., Loutre, M. F., and DeHant, V., 1989b, Influence of the changing lunar orbit on the astronomical frequencies of pre-Quaternary insolation patterns: Paleoceanography, v. 4, p. 555-564
Bond, G. C., and Kominz, M. A., 1984, Construction of tectonic subsidence curves for the early Paleozoic miogeocline, southern Canadian Rocky Mountains-implications for subsidence mechanisms, age of breakup, and crustal thinning: Geological Society of America, Bulletin, v. 95, p. 155-173
Chilingarian, G. V., and Wolf, K. H., 1975, Compaction of coarse-grained sediments I: Elsevier, Amsterdam, 552 p.
Croll, J., 1875, Climate and time in their geological relations--a theory of secular change in the earth's climate: Daldy, Tsbister & Co., London, 577 p.
Fischer, A., 1964, The Lofer cyclothems of the Alpine Triassic; in, Symposium on Cyclic Sedimentation, D. F. Merriam, ed.: Kansas Geological Survey, Bulletin 169, p. 107-149 [available online]
Fischer, A., 1986, Climatic rhythms recorded in strata: Annual Reviews of Earth and Planetary Science, v. 14, p. 351-376
Gilbert, G. K., 1895, Sedimentary measurement of geologic time: Journal of Geology, v. 3, p. 121-127
Ginsburg, R. N., 1989, Planning global research on the Cretaceous: Episodes, v. 12, p. 39
Goldhammer, R. K., Dunn, P. A., and Hardie, L. A., 1987, High frequency glacio-eustatic sea level oscillations with Milankovitch characteristics recorded in the Middle Triassic platform carbonates in northern Italy: American Journal of Science, v. 287, p. 853-892
Goldhammer, R. K., Dunn, P. A., and Hardie, L. A., 1990, Depositional cycles, composite sea-level changes, cycles stacking patterns, and the hierarchy of stratigraphic forcing--examples from Alpine Triassic platform carbonates: Geological Society of America, Bulletin, v. 102, p. 535562
Goodwin, P. W., and Anderson, E. J., 1985, Punctuated aggradational cycles--a general hypothesis of episodic stratigraphic accumulation: Journal of Geology, v. 93, p. 515-533
Grotzinger, J. P., 1986, Cyclicity and paleoenvironmental dynamics, Rocknest platform, northwest Canada: Geological Society of America, Bulletin, v. 97, p. 1,208-1,231
Haq, B. U., Hardenbol, J., and Vail, P. R., 1987, Chronology of fluctuating sea levels since the Triassic: Science, v. 235, p. 1,156-1,167
Herbert, T. D., and Fischer, A. G., 1986, Milankovitch climatic origin of mid-Cretaceous black shale rhythms in central Italy: Nature, v. 321, p. 739-743
Kauffman, E. G., 1988, Concepts and methods of high-resolution event stratigraphy: Annual Reviews of Earth and Planetary Science, v. 16, p. 605-654
Kominz, M. A., and Bond, G. C., 1990, A new method of testing periodicity in cyclic sediments--application to the Newark Supergroup: Earth and Planetary Science Letters, v. 98, p. 233-244
Kukal, Z., 1990, The rate of geological processes: Earth Science Reviews, v. 28, p. 5-284
Lawson, C. L., and Hanson, R. J., 1974, Solving least squares problems: Prentice-Hall, Englewood Cliffs, New Jersey, 340 p.
Luttrell, G. W., 1989, Stratigraphic nomenclature of the Newark Supergroup of eastern North America: U.S. Geological Survey, Bulletin 1572, 136 p. [available online]
Menke, W., 1989, Geophysical data analysis--discrete inverse theory: rev. ed., Academic Press, New York, 289 p.
Olsen, P. E., 1984, Comparative paleolimnology of the Newark Supergroup--a study of ecosystem evolution: Ph.D. dissertation, Yale University, New Haven, Connecticut, 726 p.
Olsen, P. E., 1986, A 40-million-year lake record of early Mesozoic orbital climatic forcing: Science, v. 234, p. 842-848
Olsen, P. E., McDonald, N. G. and Schlische, R. W., 1989a, Stop 7.2--Ct 9 road cut, East Berlin, Ct.; in, Tectonic, Depositional, and Paleoecological History of Early Mesozoic Rift Basins, Eastern North America, P. E. Olsen, R. W. Schlische, and P. J. Gore, eds.: 28th International Geological Congress, Field Trip Guidebook T351, American Geophysical Union, Washington, DC, p. 110-113
Olsen, P. E., Schlische, R. W., and Gore, P. J., eds., 1989b, Tectonic, depositional, and paleoecological history of early Mesozoic rift basins, eastern North America: 28th International Geological Congress, Field Trip Guidebook T351, American Geophysical Union, Washington, DC, 174 p.
Read, J. F., and Goldhammer, R. K., 1988, Use of Fischer plots to define third-order sea-level curves in Ordovician peritidal cyclic carbonates, Appalachians: Geology, v. 16, p. 895-899
Ross, C. A., and Ross, J. R. P., 1988, Late Paleozoic transgressive-regressive deposition; in, Sea-Level Changes--An Integrated Approach, C. K. Wilgus, B. S. Hastings, C. G. Kendall, H. W. Posamentier, C. A. Ross, and C. Van Wagoner, eds.: Society of Economic Paleontologists and Mineralogists, Special Publication 42, p. 227-259
Schlager, S. O., 1981, The paradox of drowned reefs and carbonate platforms: Geological Society of America, Bulletin, v. 92, p. 197-211
Schlische, R. W., and Olsen, P. E., 1990, Quantitative filling model for continental extensional basins with applications to early Mesozoic rifts of eastern North America: Journal of Geology, v. 98, p. 135-155
Smith, D. G., 1989, Milankovitch cyclicity and the stratigraphic record--a review: Terra Nova, v. 1, p. 402-404
Thomson, D. J., 1982, Spectrum estimation and harmonic analysis: Proceedings of the Institution of Electrical Engineers, v. 70, p. 1,055-1,096
Vail, P. R., Mitchum, R. M., and Thompson, S., III, 1977, Seismic stratigraphy and global changes of sea level--pt. 3, relative changes of sea level from coastal onlap; in, Seismic Stratigraphy-Applications to Hydrocarbon Exploration, C. E. Payton, ed.: American Association of Petroleum Geologists, Memoir 26,p.83-97
Van Houten, F. B., 1964, Cyclic lacustrine sedimentation, Upper Triassic Lockatong Formation, central New Jersey and adjacent Pennsylvania; in, Symposium on Cyclic Sedimentation, D. F. Merriam, ed.: Kansas Geological Survey, Bulletin 169, v. 2, p. 497-531 [available online]
Van Houten, F. B., 1969, Late Triassic Newark Group, north-central New Jersey, and adjacent Pennsylvania and New York; in, Geology of Selected Areas in New Jersey and Eastern Pennsylvania, S. S. Subitzki, ed.: Rutgers University Press, New Brunswick, New Jersey, p. 314-347
Kansas Geological Survey
Comments to webadmin@kgs.ku.edu
Web version April 21, 2010. Original publication date 1991.
URL=http://www.kgs.ku.edu/Publications/Bulletins/233/Kominz/index.html