Kansas Geological Survey, Bulletin 233, p. 489-508
by
P. Kaufman, J. P. Grotzinger, and D. S. McCormick
Massachusetts Institute of Technology
An algorithm has been developed to simulate sediment dispersal on shallow marine siliciclastic, carbonate, and mixed siliciclastic-carbonate shelves. The algorithm is based on a diffusion scheme in which the diffusion coefficient decays exponentially with water depth. The rationale for using a varying diffusion coefficient lies in the observation that on marine shelves wave energy and therefore bed shear stress decay exponentially with water depth. Thus sediment flux cannot be modeled by a diffusive process based on a linear dependence on slope alone. This approach is probably most appropriate for wave-dominated shelves. The model simulates deposition in two dimensions. Siliciclastic shelf sedimentation occurs solely by lateral transport in the plane of section by diffusion; carbonate sedimentation occurs by depth-dependent in situ sediment production with subsequent lateral dispersal of sediment by diffusion. The effects of early cementation can be modeled by varying the transport coefficient that governs the efficiency of diffusion.
An Acrobat PDF file containing the complete paper is available (1.5 MB).
A variety of forward models of basin-scale stratigraphy recently have been published. Many are two-dimensional, and several incorporate sophisticated algorithms that adequately treat basin subsidence and compound sea-level functions. Algorithms to simulate tectonic subsidence range from simple rotating hinge models to theoretically comprehensive uniform and nonuniform extension models (Lawrence et al., 1990) and flexural models (Flemings and Jordan, 1989b). Isostatic compensation of sediment loads by lithospheric flexure has also been implemented (Aigner et al., 1989; Read et al., this volume) along with routines for estimating effects of sediment compaction (Strobel et al., 1990; Read et al., this volume). Such models have significantly advanced the understanding of several variables that influence the stratigraphic architecture of sedimentary basins and are useful in extending incomplete data sets for exploration-scale operations.
At the basin or exploration scale the current generation of two-dimensional models vastly improves on previous ones [e.g., Harbaugh (1966) and Read et al. (1986)]. However, the models are still limited in their simulation of sub-basin-scale stratigraphic architecture and therefore are ineffective predictors of reservoir geometry or heterogeneity. The principal shortcomings of current numerical models are their lack of treatment of sedimentation in three dimensions and over generalization of sedimentation processes. The implementation of three-dimensional models is restricted primarily by the enormous increase in computational resources necessary for an additional spatial dimension. On the other hand, the lack of rigorous treatment of sedimentation stems from the lack of adequate theory explaining the complex process of sedimentation from first principles. Consequently, all sedimentation schemes represent compromise situations that are justified by using empirical observations of time-averaged sedimentation rates or depositional geometries. Because most models run with time steps of a hundred years or more, the physics of sediment transport is neglected and averaged sedimentation rates or depositional geometries are commonly used as proxies for physical sedimentation.
In carbonate simulations sedimentation rates are commonly defined as a function of water depth [e.g., Grotzinger (1986), Read et al. (1986), Goldhammer et al. (1987), and Gildner and Cisne (1989)]. In siliciclastic models sediment is transported by defining a flux from a point source and then distributing the sediment as a function of time by either geometric rules (Jervey, 1988; Strobel et al., 1990) or the process of diffusion (Kenyon and Turcotte, 1985; Flemings and Jordan, 1989b). Another approach assigns exponentially decreasing sedimentation rates relative to a migrating point source (Lawrence et al., 1990). In all these models a depositional facies is assigned according to the water depth computed to exist at the end of each time step for each point across the basin.
An entirely different approach is to make sedimentation and the deposited grain size functions of current velocity, where velocity decreases away from a point source as water depth increases; facies are then a function of grain size (Bitzer and Harbaugh, 1987). Other models have attempted to adapt simplified versions of the Navier-Stokes equations to reconstruct oceanic or tidal circulation in basins of known geometry (Ericksen et al., 1989; Ericksen and Slingerland, 1990) or to model transport of clastic sediment in hypothetical basins (Tetzlaff and Harbaugh, 1989). The main difference between carbonate and clastic models is that clastic models invoke a flux of sediment from a point source, whereas carbonate models utilize in situ sediment production with a depth-dependent sedimentation rate. Furthermore, most published carbonate models do not allow for lateral transport of sediment. An exception to this is Lawrence et al.'s (1990) model, which treats carbonate transport exactly the same as siliciclastic sediment.
Here we show that the diffusion scheme, given some modification, can be applied to shallow marine depositional systems in which wave processes dominate. In addition to siliciclastic settings, our approach applies to carbonate environments in which sediments are produced in situ but subsequently are transported laterally to sites where shoals or tidal flats can develop. Furthermore, the effects of early cementation can be simulated by varying the transport coefficient that governs the efficiency of diffusion. The algorithm developed here is generally applicable and can be incorporated within any two-dimensional model.
The classical diffusion equation relates the time rate of change of some property, such as temperature or momentum, to differences in gradients of that property across some spatial dimension. Geologists have recast the diffusion equation to describe the time-dependent evolution of landforms:
δh / δt = δ/δx (D δh / δx), (1)
where h is height above a horizontal datum, t is time, x is horizontal distance, and D is the diffusion coefficient that relates slope to discharge. The diffusion equation is derived by combining the continuity equation (conservation of mass) with a sediment transport function in which sediment discharge is related to slope by a constant of proportionality D. For a constant diffusion coefficient D, Eq. (1) simplifies to
δh / δt = D (δ2h / δx2), (2)
The diffusion model has been applied effectively to model a variety of time-dependent geomorphic processes, including hillslope creep (Culling, 1965), transport in alluvial channels (Begin et al., 1981), deltaic deposition (Kenyon and Turcotte, 1985), and erosion of mountain belts and evolution of foreland basins (Flemings and Jordan, 1989b). In addition, diffusion has been used to describe the transport of sediment on the eastern North American shelf (Swift et al., 1986), which Clarke et al. (1983) incorporated into a numerical model simulating the evolution of this shelf area.
Of the various approaches that have been used so far to describe the lateral transport of sediment as a time-averaged process on time scales of >100 years, diffusion is preferable to purely geometric approaches because it does not specify in advance the final state of important features, such as the geometry of stratigraphic bounding surfaces, the limitations of accommodation space, the volume of sediments that must be deposited, or final depositional slopes. Rather, the diffusion scheme is based on the premise that the rate of transport is linearly proportional to gradients in material or energy. Consequently, for problems dealing with the transport of sediment in which gradients (e.g., energy, slope, light, nutrients) determine sediment movement or production, the diffusion scheme is a good approximation of the time-averaged sediment dispersal process. For our model depositional slope is assumed to be the gradient that drives the diffusive process.
Our model differs from previous ones that have used diffusion for marine environments [e.g., Flemings and Jordan (1989b) and Kenyon and Turcotte (1985)] in that we employ an exponentially decaying water-depth-dependent diffusion coefficient. Diffusion models with constant diffusion parameters (Begin et al., 1981; Culling, 1965; Kenyon and Turcotte, 1985) have been used for simulating subaerial landform evolution because of the reasonable simplification that runoff and sediment flux are linearly proportional to slope [although see Paola (1990)]. Our rationale for using a varying diffusion coefficient lies in the observation that the wave energy available to mobilize sediment on a marine shelf decays exponentially with water depth, as shown by Airy wave theory (Allen, 1985; Clarke et al., 1983), and thus sediment flux probably is not well modeled by a linear dependence on slope alone. We combine the depth-dependent effect of wave energy available for mobilization of sediment with the slope-dependent effect of gravity, which on average would tend to redistribute entrained sediment downslope. Geologic support for this approach is provided by Leckie and Krystinik (1989, 1991), who show that transport of sediment on many ancient wave-dominated shelves occurred in a predominantly offshore, downslope direction.
The model simulates deposition in two spatial dimensions. Siliciclastic shelf sedimentation occurs solely by lateral transport in the plane of section by diffusion; carbonate sedimentation occurs by depth-dependent in situ sediment production with subsequent lateral sediment diffusion. Elements common to both types of sedimentation are the way in which sea level, initial water depth, tectonic subsidence, and transport of clastic particles are treated. The model runs with a free boundary on the seaward end; any sediment that reaches the free boundary will be flushed out of the section. Because it is only the effect of variable sediment diffusion that we wish to examine here, the model does not contain second-order features, such as sediment compaction, sediment-induced loading, isostatic compensation and flexure, or sedimentation lag times. However, these features can be easily appended to the fundamental algorithm presented here.
An analytical solution to the diffusion equation for constant D, as constrained by the boundary conditions used here, is developed in appendix A. It is a more completely developed solution than the one presented by Kenyon and Turcotte (1985), which does not account for subsidence or initial water depths and which also assumes a constant geometry for depositional slope. Furthermore, Kenyon and Turcotte used a moving boundary that is maintained at a constant elevation, in contrast to our model, which maintains constant flux at the landward boundary. The analytical solution for diffusion with a nonlinear dependence of D on water depth is currently not possible without the aid of numerical integration (Crank, 1975, p. 112). Thus we solve the problem numerically using an implicit finite-difference approach (see appendix B), which is the subject of this article.
The diffusion equation is solved implicitly by the Crank-Nicholson method because it is more stable than explicit schemes for all sizes of spatial and time steps (Incropera and DeWitt, 1985; Press et al., 1986). Greater stability implies less sensitivity to small numerical perturbations caused by computational round-off errors. This is not to say that perturbations do not occur, but the implicit Crank-Nicholson scheme prevents them from growing catastrophically, as occurs in explicit finite-difference methods. The irregularities of time lines in some of the plots are numerical artifacts and should not be interpreted as sedimentologic features. These small irregularities would be suppressed by using smaller time and spatial steps in the computational grid. Because we are using an implicit method to solve a nonlinear diffusion equation, we must solve for the diffusion coefficient iteratively as a series of coupled nonlinear equations by Newton's method for each time step, as outlined by Press et al. (1986) and Strang (1986).
Several processes influence the facies and geometry of stratigraphic sequences. The effects of subsidence and sea level have been discussed at length and are most important in controlling the distribution of accommodation space through time across the platform. In our model sedimentation is simulated as a diffusive process and the transport coefficient D controls the efficiency of this process. In contrast to previous diffusion models, we modify this term to include an exponential dependence of D on water depth. This leads to the relation
D = C0 exp(-C1W), (3)
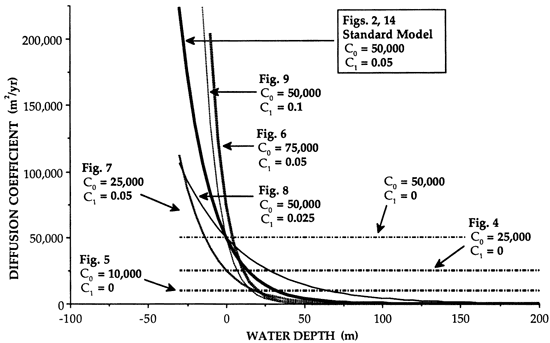
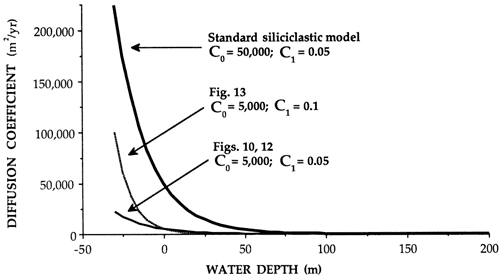
where D is the transport (diffusion) coefficient, W is water depth, C0 is the diffusion constant at sea level (W = 0), and C1 is a decay constant that controls how steeply D decays with increasing water depth. Thus C0 and C1 can be varied systematically to produce different transport parameters that affect the rate of diffusion and its depth dependence. The relationships between D and W for different values of C0 and C1 are shown in figs. 1 and 11.
Other important variables are the rate at which sediment enters the basin (flux) and the locations where sediment enters the basin. Siliciclastic sediment is modeled by introducing material from a single point source on one side of the basin, whereas carbonates are generated by adding material at every point in the basin, with a production rate dependent on water depth. We use two carbonate production functions, a ramp model and a rimmed shelf function, similar to those used by Gildner and Cisne (1989). In addition, the sedimentation rate for the carbonate model can be enhanced at specific positions on the shelf relative to surrounding regions by multiplying the production rate by some constant factor, simulating reef or shoal development.
Figure 1--Relationship between water depth and diffusion coefficient D for D = C0e-C1W, as discussed in text. These curves apply to the siliciclastic model runs. Because of the exponential form of the curves, D is sensitive to small changes in water depth in shallow regions, tapering off sharply at deeper water depth. Increasing C0 effectively increases the efficiency of the diffusion process and, by implication, lateral transport of sediment. Increasing C1 causes D to decay more sharply with water depth; this decreases the efficiency of the diffusion process at greater depths. As C1 is decreased, the disparity between sediment transport efficiency at different depths is significantly decreased. When C1 = 0, D is a constant and independent of water depth.

The following examples illustrate the effect that varying the diffusion parameters individually has on stratigraphic geometry; other parameters (e.g., sea level and subsidence) are set to the standard model values (table 1) unless otherwise specified. Runs are shown for both siliciclastic and carbonate shelves.
Table 1--Explanation of parameters used in siliciclastic model
| Model Parameter |
Method Used |
Standard Model |
Ranges in Trials |
|---|---|---|---|
| Initial water depth (m) | Linearly increasing | 10 (left) 30 (right) |
No change from standard |
| Tectonic subsidence (cm/k.y.) |
Linearly increasing | 10 (left) 20 (right) |
No change from standard |
| Sea level | Sinusoidal | 5 m amplitude 50 k.y. period |
5 or 10 m amplitude Single period of 50 k.y. or compound periods of 20, 40, and 80 k.y. |
| Diffusion coefficient [Eq. (3)] |
Depth-dependent and exponentially decaying |
C0 = 50,000 C1 = 0.05 |
C0 = 10,000-75,000 C1 = 0-0.1 |
| Sediment flux (m2/yr) | Constant input on landward (left) side |
10 | 5-20 |
A standard model is shown in fig. 2 and is used for the purpose of comparison; model parameters are shown in table 1. Figure 3 shows the form of the sea-level curves used in the simulations. Each run starts at the maximum rate of rise, and time lines are printed every 12.5 k.y., thus corresponding to the maximum rate of rise, highstand, maximum rate of fall, and lowstand for each 50k.y. period. Note that the maximum progradation occurs during each lowstand (e.g., 87.5-k.y. time line in fig. 2) rather than at the time of maximum rate of fall (e.g., 75 k.y.). A similar result was obtained by Angevine (1989) and Flemings and Jordan (1989a). The maximum amount of erosion also occurs during the lowstand. During the subsequent sea-level rise, a condensed sequence and the maximum backstepping of facies onto the shelf occur at the time of sea-level highstand (e.g., 112.5 k.y.), not at the time of maximum rate of rise. Aggradation of the shelf is most pronounced between the maximum rate of rise and the maximum rate of fall (e.g., 100-125 k.y.). Note that the depositional slope steepens into the deepest part of the basin where sediment transport is lower. This is because the calculated diffusion constant is lower for greater water depths, in accordance with Eq. (1).
Figure 2--Standard run showing effects of depth dependency on sediment transport. All parameters of the standard model are shown in table 1. Lines within the plots are time lines spaced at intervals of 12.5 k.y. Time lines in all subsequent plots except fig. 14 are spaced at identical intervals. Numbers along time lines within plots indicate the age in kiloyears since beginning of model run. The time line to which the date belongs corresponds to the time line that forms the diameter of the white circle. Note truncation of time lines on the landward end of the profile, indicating erosion during lowstands when D is highest. An example of a surface of maximum truncation occurs along the 87.5-k.y. time line at the lowstand in the sea-level curve, not at the inflection point (time of maximum rate of fall), which occurs at 75 k.y.
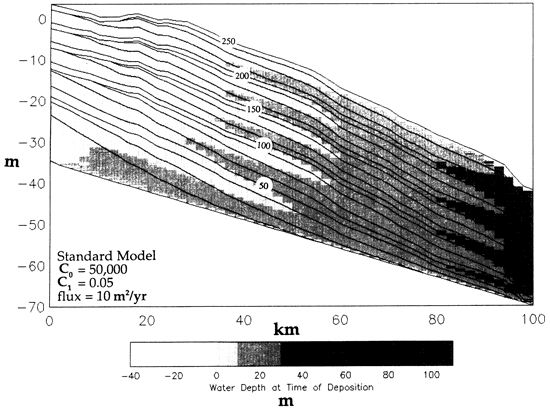
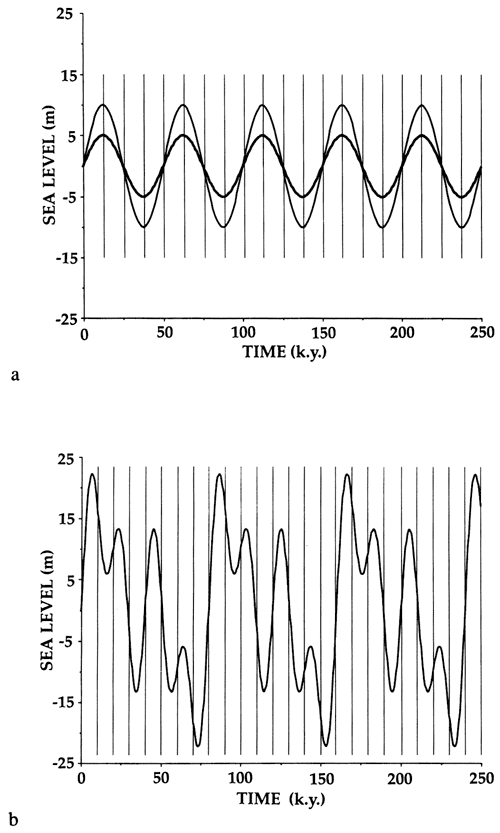
Figure 3--(a) Model sinusoidal sea-level curves with 5 m and 10 m amplitude and constant periods of 50 k.y. Vertical lines correspond to the time lines on the model plots at intervals of 12.5 k.y. (b) A compound sea-level curve, used exclusively for fig. 14, that consists of 3 sinusoids, each with an amplitude of 10 m and periods of 20 k.y., 40 k.y., and 80 k.y. Vertical lines correspond to the time lines in fig. 14 at intervals of 10 k.y.
As C, approaches 0, the exponential term diminishes and the relationship between W and D becomes increasingly linear and eventually constant (i.e., D = C0; see fig. 1). Figure 4 illustrates the case when C1 = 0. The spacing of the time lines shows that the accumulation of sediment does not depend on water depth. There is no variation in amount of erosion across the platform, as shown by the lack of truncation of time lines. Sediments pass with equal efficiency between different water depths; however, the facies belts migrate laterally in phase with sea-level changes. As in fig. 2, maximum progradation of facies corresponds to sea-level lowstand (e.g., 37.5 k.y.), and maximum retrogradation corresponds to sea-level highstand (e.g, 62.5 k.y.). The result is a concave-up slope, unlike most modern shelves. On modern shelves there is a nearly linear increase in water depth to the outer part of the shelf, and a concave-down slope is associated with an increase in slope declivity into greater water depths.
In fig. 4 a value of 25,000 was used for C0. This value is consistent with empirical determinations of D for deltaic systems, as tabulated by Flemings and Jordan (1989b). In contrast, this value is changed to C0 = 10,000 in fig. 5 for comparison. Note that the higher C0 (fig. 4) results in more efficient transport of sediment into the basin and less aggradation on the landward end of the profile; the profile reaches a steady-state uniform slope within the duration of the model run. Note also that with higher D (fig. 4), the steady-state uniform slope is lower than the steady-state slope toward which fig. 5 evolves.
Figure 4--The effect on sediment dispersal patterns when C1 = 0 and C0 = 25,000. In this case D has no dependence on water depth. Sedimentary facies belt migrates in phase with sea-level variations. Compare with fig. 2, where all other parameters are the same except for C1 and a 10-m-amplitude sea-level curve.
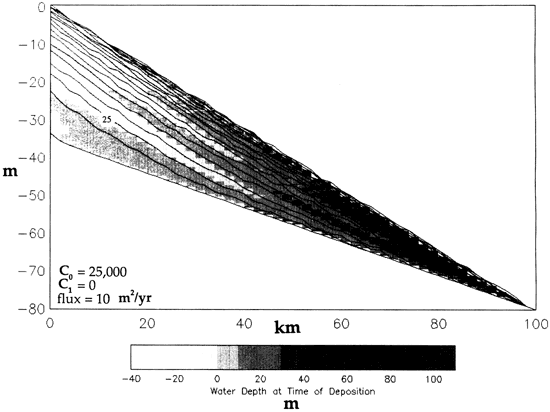
Figure 5--Model run with C1 = 0 and C0 decreased to 10,000. This results in less efficient dispersal of sediment and an increase in depositional slope and shallowing to persistent alluvial sedimentation. Compare with fig. 4, where slopes are less steep and sediments are deposited in deeper water on average. A 10-m-amplitude sea-level curve is used.
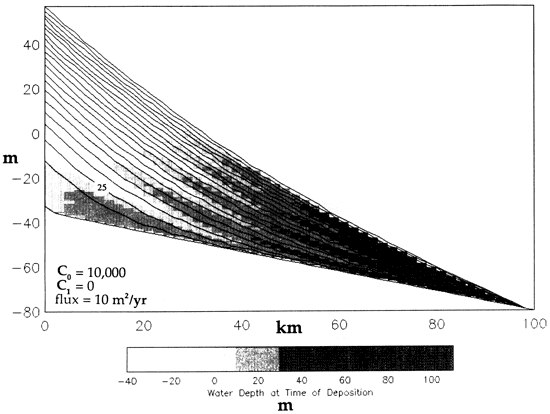
In both figs. 4 and 5 the apparent pinchout of the sediments just before the boundary of the plot at 100 km is a numerical artifact of the right-hand boundary condition of this finite-difference model. The boundary condition stipulates that all sediment entering the last column leaves that column at the same rate. This condition is obtained by forcing the slope at the right-hand boundary to be constant over the last three columns. Therefore the spatial derivative of the slope, δ2h/δx2, equals 0 and the height of that column does not change. As a result, any sediment entering the second to last column passes through the right-hand boundary and no aggradation occurs, causing the convergence of all time lines at the second to last column. The smaller area occupied by the stratigraphic cross section in fig. 4, compared to fig. 5, reflects the fact that a greater amount of sediment bypassing occurs because more sediment reaches the right-hand boundary. Because the sediment diffuses more efficiently across the profile for a higher value of D (fig. 4), it aggrades less, greater lateral dispersal takes. place, more bypassing at the right-hand boundary occurs, and consequently deeper-water conditions result more frequently.
Figures 6 and 7 show the effects of increasing and decreasing C0 for a fixed value of C1 (0.05 = standard model). Changing the value of C0 alters the efficiency of sediment diffusion by the same factor at all water depths. Because of the exponential dependence on water depth, the diffusion of sediment is far less effective at deeper water depths than for constant diffusion coefficient (compare curves in fig. 1). Consequently, shelf slopes are concave down rather than concave up, as in the case of constant D (figs. 4 and 5).
As C0 decreases from 75,000 (fig. 6) to 25,000 (fig. 7), diffusion of sediment becomes less efficient at all water depths, resulting in aggradation of coastal plain facies and steepening of the shelf profile. The decreased value of C0 results in an overall long-term progradation in contrast to the long-term aggradation that develops for a higher value of C0 (fig. 6). In both cases, short-term progradation and retrogradation correspond to the lowstand and highstand of sea level, respectively (e.g., 87.5 k.y. and 112.5 k.y.). Furthermore, incision and development of sequence boundaries occurs during the lowstand (87.5 k.y.).
Figure 6--Model run in which C0 is increased to 75,000 and all other parameters are as in the standard model, including a value of 0.05 for C1. Because C1 is now greater than 0, D depends on water depth. Note how the high value of C0 results in highly aggradational, tabular deposits.
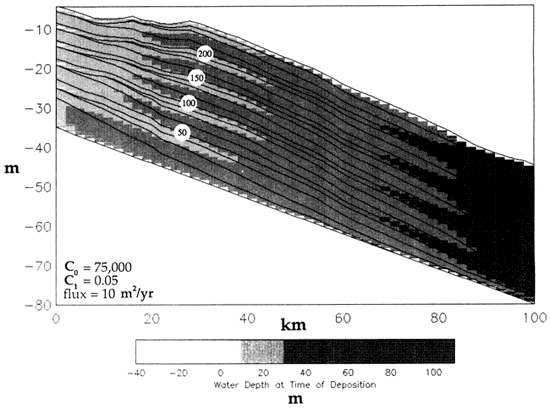
Figure 7--Model run with conditions the same as in fig. 6, except that C0 is decreased to 25,000. Note the enhanced wedge shape of the deposits, concave-down slopes, and progradational facies patterns.
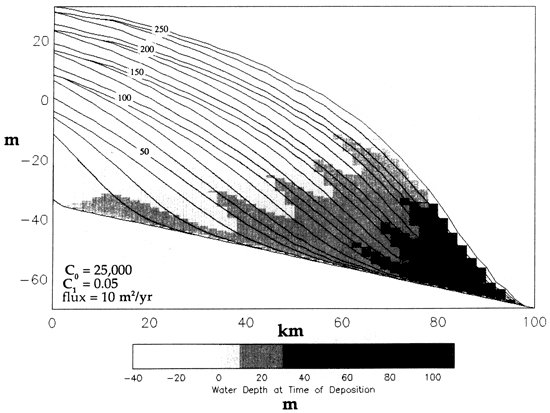
Figures 6 and 7 illustrate how the model can be used to simulate the difference in sediment transport on high-energy versus low-energy coastlines. The increased current activity (wave-induced, tidal, or oceanic) associated with high-energy settings often results in more effective transport of sediment to deeper water positions. This could be simulated by increasing C0, thereby improving the efficiency of sediment transport at all water depths.
Figures 6 and 7 illustrate how the model can also be used to simulate the difference in sediment transport on muddy versus sandy shelves. Low values of C0 mimic low erodability of the substrate, which would correspond to muddy, cohesive shelves with vegetated subaerial areas. High values of C0 mimic more easily eroded material, such as that associated with sandy, noncohesive shelves with nonvegetated subaerial regions.
Variations in C1 have a profound effect on sediment transport and shelf morphology. As C1 approaches 0, the diffusion coefficient D depends less on water depth until, when C1 = 0, D is constant. Consequently, for small values of D the model more closely approximates the constant D situation (e.g., fig. 4). Figure 8 shows an experiment in which C1 is reduced to 0.025, compared to 0.05 for the standard model. As a result, the stratigraphy in fig. 8 is closer to that in fig. 4 than to that in fig. 2, particularly with regard to the depositional slope. Larger values of C1 favor increasingly concave-down depositional slopes, as shown in fig. 9. In particular, note that, because of the exponential decay (see fig. 1, curve that shows C1 = 0.1), the inner shelf slopes stay relatively gentle but the outer shelf slopes increase sharply as water depth increases. More sediment is stored in the shallow-water part of the shelf.
Figure 8--Model run showing effect of decreasing C1 to 0.025. See text for discussion.
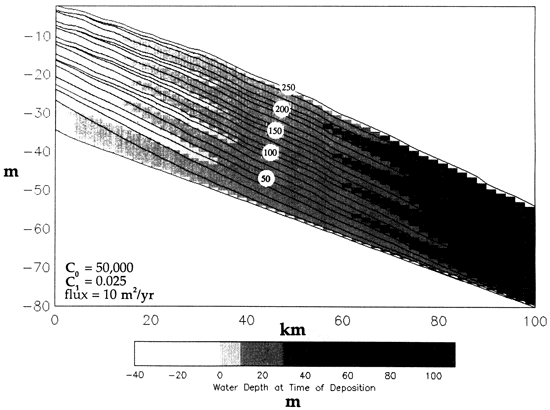
Figure 9--Model run with C1 increased to 0.1. Note the pronounced increase of shelf gradients into deeper water resulting from the dependence of D on water depth. Compare with fig. 8. See text for further discussion.
Slope steepening results because, as water depth increases, the efficiency of the diffusion process decreases exponentially and less sediment is transported laterally per unit of time. For higher values of C1, the efficiency of the diffusion decreases more rapidly at greater water depths. The shelf aggrades, but the basin is left behind. Eventually, however, the slope becomes so steep that the topographic gradient causes increased flux into the basin despite the fact that D is very low for the water depths represented by the slope and basin. This is shown by the sediment distribution for the last two time lines in fig. 9, in which there is an abrupt increase in thickness per unit time in the deepest parts of the basin compared to previous time intervals.
The effect that C1 has on D and on the geometry of stratigraphic units, contrasted in figs. 8 and 9, is our principal point here. Depth-dependent diffusion generates a geologically meaningful approximation of depositional transects associated with shallow marine and shelf to basin transects. Slopes simulated by this model result from a model of a physical process rather than from an arbitrary construct based on empirical rules about depositional geometry. The C1 parameter can be changed to simulate the difference in sediment transport on high- versus low-energy shelves. Reduced shelf sediment transport, associated with low-energy settings, can be simulated by increasing C1 and decreasing the efficiency of sediment transport at moderate to deep water depths. More sediment introduced at the landward end is stored in the shallow marine portion of the shelf. This has the qualitative effect of simulating a shallow wave base.
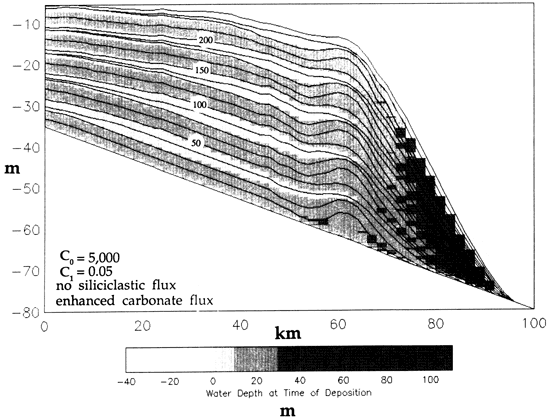
Ramp model Figure 10 illustrates the stratigraphy of a carbonate ramp. The input parameters for this trial and the succeeding carbonate and mixed clastic-carbonate trials are shown in table 2. In this case all sediment influx is from below, unlike the siliciclastic model in which all influx was from the landward side. Sediment aggradation occurs in situ and is associated with lateral downslope transport of sediment, which causes progradation. As in the siliciclastic model, the limits of maximum progradation and retrogradation occur with sea-level lowstands and highstands, respectively (e.g., 87.5 k.y. and 112.5 k.y.).
Figure 10--Distally steepened carbonate ramp formed by in situ depth-dependent sediment production and simultaneous restricted lateral sediment transport. A 10-m-amplitude sea-level curve is used. See text for discussion.
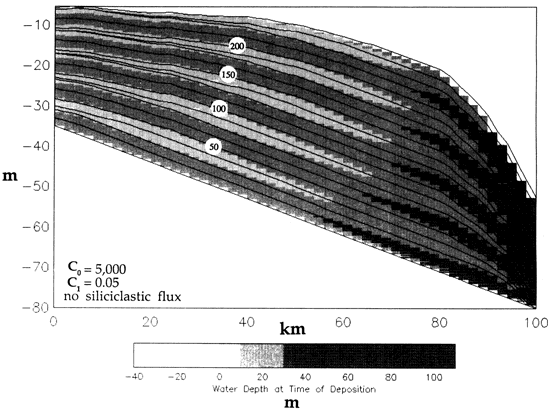
Table 2--Explanation of parameters used in carbonate models.
| Model Parameter |
Method Used |
Ramp Model |
Rimmed Shelf Model |
Mixed Clastic-Carbonate Model |
|---|---|---|---|---|
| Initial water depth (m) | Linearly increasing | 10 (left) 30 (right) |
No change from ramp | No change from ramp |
| Tectonic subsidence (cm/k.y.) |
Linearly increasing | 10 (left) 20 (right) |
No change from ramp | No change from ramp |
| Sea level | Sinusoidal | 10 m amplitude 50 k.y. period |
No change from ramp | No change from ramp |
| Diffusion coefficient [Eq. (3)] |
Depth dependent and exponentially decaying |
C0 = 5,000 C1 = 0.05 |
C0 = 5,000 C1 = 0.05 |
C0 = 5,000 C1 = 0.1 |
| Sedimentation rate (regular) |
Carbonate: in situ from seafloor (bottom) and depth dependent |
Carbonate = step function ≤0 m = 0 (cm/k.y.) >0-5 = 20 5-10 = 75 10-25 = 50 25-50 = 20 >50 = 0 |
Regular | No regular used |
| Sedimentation rate (suppressed) |
Carbonate: in situ from seafloor (bottom) and depth dependent |
No suppression used |
No suppression used |
Carbonate = step function ≤0 m = 0 (cm/k.y.) >0-5 = 10 5-10 = 37.5 10-25 = 25 25-50 = 10 >50 = 0 |
| Sedimentation rate for reefs (enhanced) |
Multiply regular or suppressed sedimentation rates by factor of 1-10 |
No enhancement | 4x regular for reef | 4x regular for reef |
| Width of carbonate factory | Assign position(s) anywhere between x = 1 and 96 in computational grid |
Production occurs between x = 1 and 96 at regular sedimentation rates |
Reef for x = 60-64 Regular for x = 1-59 |
Reef for x = 60-64 Suppressed for x = 20-59 |
| Sediment flux of siliciclastics (for mixed clastic-carbonate model) |
Siliciclastic: constant input on landward (left) side |
None | None | 1 m2/yr |
Sedimentation rates are water depth dependent, and sediment production occurs over the entire shelf in contrast to the point source of the siliciclastic model. Lower values of C0 (by an order of magnitude; see fig. 11) were chosen arbitrarily to simulate lower erodability of carbonate sediment as a result of a variety of processes. For lower values of C0 less sediment is removed after it is produced, thereby simulating decreasing erodability. In a future version of this model variable diffusion coefficients for different sediment types will be implemented. This will allow us to simulate highly mobile substrates, such as ooid shoals. In that case the value of C0 will be increased relative to surrounding regions to simulate rapid lateral spreading of the shoal.
Figure 11--Comparison of diffusion coefficient with water depth used in the carbonate model runs. The standard siliciclastic model curve is plotted for comparison (cf. fig. 1). Lower values of C0 result in a much lower diffusion coefficient at a given depth and thus in much slower sediment dispersal. This condition is used to mimic early cementation of carbonate materials.
The diffusion coefficient D is also depth dependent, as in the siliciclastic model, and C1 can be varied to simulate reduced sediment dispersal at depth. By increasing the value of C1, sediments will be less efficiently transported at greater depths, resulting in slope steepening. This can be used to simulate distally steepened ramps, such as that shown in fig. 10. If the value of C1 is reduced, the ramp geometry will become more homoclinal with lower curvature of the profile because of the increased efficiency of sediment transport at depth.
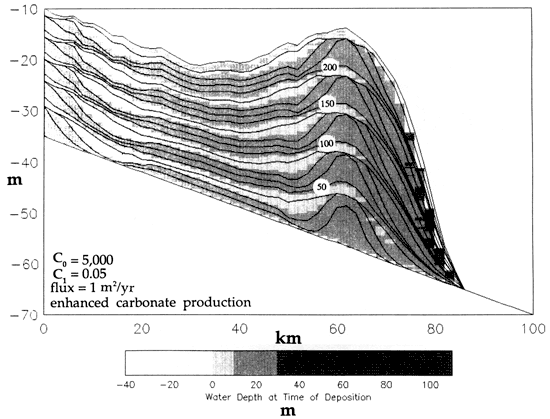
Rimmed shelf model Figure 12 shows the results of a run in which a zone of high sediment production is located in an outer shelf position to form a reef barrier. Reef sediment production rates are 4 times higher between 60 km and 64 km (37-40 mi) than those in the landward area. No carbonate production occurs seaward of the reef, illustrating the effects of downslope transport of reef material by diffusion. All other parameters are identical with the ramp model shown in fig. 10.
Figure 12--Rimmed carbonate shelf highlighting enhanced carbonate production at the shelf edge between 60 km and 64 km. A 10-m-amplitude sea-level curve is used. See text for discussion.
It is interesting to note the first-order similarity between this shelf geometry and the Permian platform of West Texas [cf. Dunham (1969)], where the reef is several meters deeper than the backreef facies belts. This topography can be reversed if the sediment production rates are increased for the reef and/or the sediment production rates for the landward zone are reduced. The steepness of the slope on the seaward side of the barrier reef can be controlled to mimic greater or lesser amounts of early cementation by changing the value of C1; if C1 is higher, then the efficiency of lateral transport at depth is decreased and the slope steepens.
Finally, well-developed cyclic carbonate facies interfinger with the reef complex, similar to many modern and ancient rimmed carbonate platforms. The shallowest water facies of the cycles are symmetrically distributed about the time line representing the lowstand in sea level for each sea-level oscillation (e.g., 87.5 k.y.).
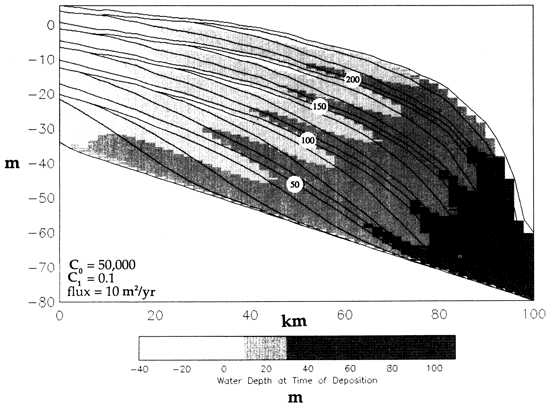
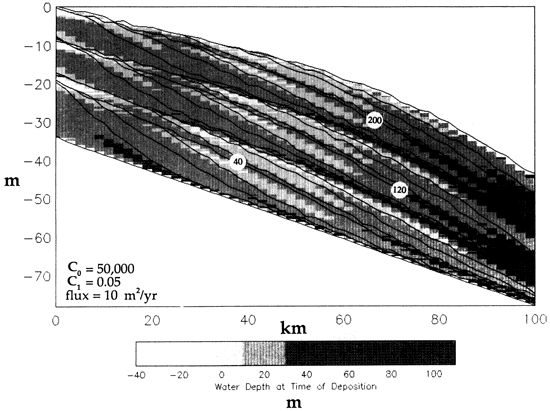
Although superficially similar to the carbonate model in fig. 12, the mixed model in fig. 13 is substantially different. In this model run there are 3 different modes of sedimentation: siliciclastic influx from the landward side, reduced carbonate sedimentation between 20 km and 59 km (12-37 mi), and enhanced carbonate production between 60 km and 64 km (37-40 mi). As the result indicates, a reef barrier develops at an outer shelf position and supplies sediment to either side of it. At the same time, siliciclastic sediment enters from the landward side, resulting in progradation toward the reef. The intervening area is a zone of suppressed carbonate production and receives only small amounts of sediment from the reef and siliciclastic source areas; consequently, it evolves into an intrashelf basin characterized by starved sedimentation. It is interesting to note that layers of siliciclastic and carbonate peritidal sediment [patterned for water depths of 0-10 m (0-32 ft)] extend into the intrashelf basin from their point sources. Significantly, these layers are temporally equivalent to each other and, once again, are distributed symmetrically about the lowstand time lines (e.g., 87.5 k.y.). Note also the erosion of reef units and of the upslope portions of both the siliciclastic and carbonate peritidal layers during the cycle lowstands.
Another important difference between figs. 12 and 13 is the change to a higher value of C1 (0.1) in fig. 13. As discussed previously, this has the effect of increasing the slope on the seaward (right) side of the reef because of the sharp decay of the diffusion coefficient and resulting decrease in efficiency of sediment transport at depth. A comparison of the profiles in figs. 12 and 13 reveals that the slope attained in fig. 13 is steeper.
Figure 13--Mixed siliciclastic-carbonate shelf illustrating the combined effects of three zones of sediment production and lateral dispersal. There is a sediment flux from the left-hand side simulating siliciclastic input, flux from below between 20 km and 50 km to simulate lagoonal production, and enhanced flux between 60 km and 64 km to simulate reef growth. A 10-m-amplitude sea-level curve is used. See text for discussion.
An important aspect of the model is its capability to resolve stratigraphic relationships with a vertical scale of the order of meters to tens of meters. This is useful in understanding the controls that govern the distribution of facies in many cyclic sequences and is relevant to evaluating the geometry of hydrocarbon reservoirs. Although all runs are shown with a horizontal length of 100 km (62 mi), the model can be easily rescaled to illustrate features on the scale of a few kilometers.
Most runs of siliciclastic, carbonate, and mixed systems show stratigraphic units that alternate on a vertical scale of meters to tens of meters and interfinger on a scale of many tens of kilometers. In most examples these stratigraphic units form sheets or gently tapering wedges. Although this may be appropriate for some sequences, other sequences exhibit more lateral heterogeneity by forming irregular wedges and lenses. An example of a run designed to produce more complex stratigraphy by introducing multiple sea-level curves is shown in fig. 14. The results are interesting because they clearly illustrate the effect of constructively and destructively interfering sea-level curves on stratigraphy (compare figs. 3 and 14).
Figure 14--Sediment bypassing associated with complex sea-level oscillation history. Times lines are drawn every 10 k.y. Note development of discrete lenses and complex wedges of shallow-water sediments enclosed in deeper-water sediments. Also, bypassing is maximized during times of sea-level lowstand and not at times of maximum rate of fall.
The model shown in fig. 14 contains many of the features associated with lowstand shoreface deposits in ancient settings. Lenticular shallow-water to alluvial deposits are associated with erosional surfaces (note truncation of time lines, e.g., between 110 k.y. and 120 k.y.) that pass downdip into correlative conformities. Such a downward shift in shoreface stratigraphy has been documented in the Cretaceous Cardium formation by Plint (1988). The Cardium is known to contain important reservoirs developed in shoreface sandstones with complex geometries, emplaced during changes in relative sea level. As in the Cardium, our model shows that erosion, sediment bypassing, and juxtaposition of shoreface against deeper shelf facies is possible on a vertical scale of meters. Note that complete bypassing of shallow-water to alluvial facies occurs approximately one-quarter of the way across the model profile. Erosion occurs along parasequence boundaries (0, 80, 160, 240 k.y.) in response to a decrease in water depth, which increases the diffusivity of sediments, simulating higher energy conditions. The greatest erosion and bypassing occur during the maximum lowstands in sea level (e.g., 80 k.y.) and not during the maxima in rates of change (e.g., 50 or 68 k.y.). Another result is that the greatest erosion and bypassing coincide with the lowstands of the 40-k.y. and 80-k.y. sea-level cycles, whereas there is only a negligible effect associated with the 20-k.y. cycle despite the amplitudes all being set to 10 m. This result reinforces the notion that erosion and bypassing associated with high-frequency sea-level oscillations are controlled by the magnitude of sealevel lowstands rather than by rates of sea-level change [cf. Angevine (1989)].
It is interesting to note that our modeling results support the interpretation of Plint (1988) that the offshore bars in the Cretaceous western interior seaway formed as a result of sediment bypassing during sea-level lowering. During the subsequent transgression, sediment bodies formed during bypassing are further modified, with the result being a high-energy deposit enclosed within offshore deposits.
The results illustrate the application of a nonlinear water-depth-dependent diffusion model to the simulation of siliciclastic, carbonate, and mixed shallow marine depositional systems.
Models using a constant diffusion coefficient D can have only concave-up to linear slopes at equilibrium. The model developed here can generate concave-up and concave-down shelf profiles, both of which are found in real shelf cross sections (Bally, 1987; Driver and Pardo, 1974; Grow et al., 1988).
Jordan and Flemings (1991) address this problem by using two constant values for D such that more efficient diffusion (higher D) occurs in the alluvial part of the profile, whereas less efficient marine diffusion (lower D) occurs in the marine section. Their model essentially produces two coupled concave-upward profiles. The advantage of our approach is that it recognizes that sediment dispersal in the marine environment does not depend solely on slope of the shelf but is also a product of storm, ocean wave, and tidal processes whose influence decays with water depth. This depth-dependent scheme is accomplished by taking an initial diffusion coefficient (C0) and multiplying it by a function that decays exponentially with water depth. In this manner profiles are generated that mimic shallow marine shelf morphology, particularly with regard to the transition from shelf to slope settings.
Carbonates and mixed siliciclastic-carbonate settings can also be effectively modeled by using the diffusion approach. In these settings the high level of substrate heterogeneity, including early-cemented reefs and hardgrounds, highly mobile ooid shoals, and siliciclastic sands, demands an approach that can simultaneously account for varying degrees of erodability and lateral sediment dispersal. The flexibility of the diffusion algorithm makes it an effective proxy for sediment transport in models where transport results from gradients in energy or material. This method is particularly useful when material from several sources mix, such as in the runs that simulate combined siliciclastic and carbonate sedimentation.
An interesting result produced for all cases for the range of sediment fluxes and sea-level curves shown here is that the times of maximum transgression and regression correspond to the timing of the sea-level highstand and lowstand, respectively, for each oscillation in sea level. This is consistent with recent findings that show that for short periods the maximum extent of progradation of the shoreline will tend to coincide with the sea-level lowstand (Angevine, 1989; Flemings and Jordan, 1989a; Jordan and Flemings, 1991).
The depth-dependent diffusion approach does have several drawbacks. Of these, an important one intrinsic to the methodology is that, by using the exponential diffusion coefficient above sea level, values of D grow too large for elevations in excess of 20 m (64 ft) above sea level. When this value is exceeded, unrealistically high erosion and sediment transport rates will result. The actual value of D varies depending on what values of C0 and C1 are chosen (see fig. 1), but at values of C0 ≤50,000 [consistent with values used by Flemings and Jordan (1989a) and Kenyon and Turcotte (1985)], elevation of the sediment surface <20 in above sea level will not produce excessively high values of D. For this reason the model was run with sea-level amplitudes of 5 m and 10 m to ensure that elevations >20 m above sea level did not occur. A future version of this model will address this shortcoming by introducing an algorithm that uses a depth-dependent relationship for submarine values of D but a separate, probably constant value of D for subaerial sedimentation.
A more basic shortcoming of this approach is that the simulations were conducted entirely in two dimensions, whereas shelf sedimentation commonly involves significant amounts of out-of-the-plane or longshore transport of sediment. In principle, this methodology could be implemented in three dimensions but would require several orders of magnitude increase in computational time and power.
The most fundamental criticism of our approach is that longshore transport does not result from diffusive processes based on slope. The tractional transport is more realistically understood as a nonlinear function of bed shear stress (Middleton and Southard, 1984); the relation between bed shear stress and slope is not well understood for alluvial, let alone marine, environments. This suggests that our model may be more appropriate for the limiting case of siliciclastic or carbonate wave-dominated shelves where depth-dependent, exponentially decreasing wave energy mobilizes sediment. Once mobilized, sediment can be redistributed by gravity-driven flow near the sea bed directed largely by local slope.
The diffusion equation for landform evolution is derived by combining the continuity equation with a rate of sediment transport that is linearly proportional to slope. The diffusion equation becomes
δh / δt = D (δ2h / δx2), (A.1)
where h is elevation above or below a horizontal datum (here taken to be mean sea level), x is lateral distance, t is time, and D is the diffusion coefficient (Jordan and Flemings, 1990; Kenyon and Turcotte, 1985). The diffusion coefficient is constant. For a basin modeled with subsidence increasing linearly in space across the basin, additional subsidence terms must be added to Eq. (A. 1), creating
δh / δt = D (δ2h / δx2) + Y0 + Y1x. (A.2)
The sum (Y0 + Y1x) determines the rate at which the sediment surface is tectonically lowered or uplifted with respect to the datum. For (Y0 + Y1x) < 0 , subsidence occurs; for (Y0 + Y1x) > 0, uplift occurs.
Given the initial conditions
[h(x, t)]t=0 = H0 + H1x (A.3)
and boundary conditions of constant flux at x = 0 into a semi-infinite half-space
[-D(δh / δx)]x=0 = S0, (A.4)
Eq. (A.2) can be solved by using Laplace transforms in a manner analogous to that of Crank (1975).
By multiplying by e-pt in which F(p) is the Laplace transform of f(t), and integrating with respect to t from 0 to ∞, we obtain
![]()
Changing the order of differentiation and integration yields
![]()
The left-hand side of Eq. (A.6) is solved by integrating by parts:
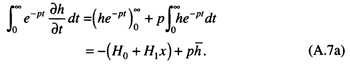
Similarly, the right-hand side yields
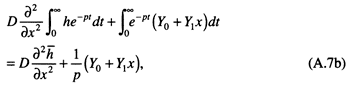
where ![]() the Laplace transform of h. This leaves an ordinary differential equation for F,
the Laplace transform of h. This leaves an ordinary differential equation for F,
![]()
that can be solved by the sum of a general solution,
![]()
and a particular solution,
![]()
Taking the part of the general solution that remains bounded as x goes to infinity yields
![]()
Using the Laplace transform on the boundary condition yields
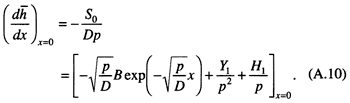
The unknown constant B is determined by algebraic manipulation:
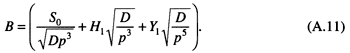
The entire solution for Eq. (A.8) with the given boundary conditions is
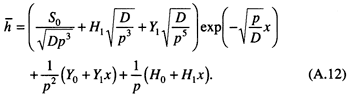
The inverse Laplace transform for ![]() is (Crank, 1975, pp. 376-379)
is (Crank, 1975, pp. 376-379)
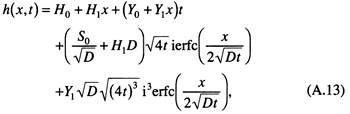
where
![]()
and
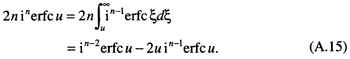
This in turn simplifies to
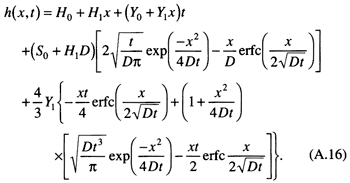
The variables in Eq. (A. 16) have the following dimensions:
H0 = length
H1 = no dimension
Y0 = length/time
Y1 = 1/time
S0 = length2/time
D0 = length2/time
The function for h(x, t) can be used alone to find time lines for various combinations of H0, H1, Y0, Y1, S0, and D. It can also be combined with a sea-level function to determine total water depth at a given time and position, from which a facies can be assigned.
The diffusion equation with differential subsidence and aggradation is
δh / δt = δ / δx[D(δh / δx)] +Y0 + Y1x + A(h,t) (B.1)
A Crank-Nicholson implicit finite-difference scheme centered at time step (n + 1/2) and space step j has second-order accuracy in time and space and is inherently more numerically stable than explicit schemes. Following the example of Press et al. (1986), we can write Eq. (B.1) in the form
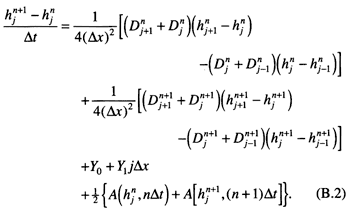
The variables Δx and Δt are the incremental space and time steps, respectively. The diffusion coefficient D in this model is defined as
D = C0 exp[-C1(SL - h)], (B.3)
where SL(t) is sea level and (SL - h) is the water depth. Values of Djn+1 for the implicit finite-difference scheme shown in Eq. (B.2) are found using the chain rule:
(δD / δt) = (δDδh / δhδt) = (δDδSL / δSLδt) = -C1D [(δSL / δt) - (δh / δt)]. (B.4)
Changing the time derivatives into their finite-difference approximations, except for sea level, which can be analytically determined from the input function, yields
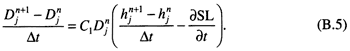
Finally,
![]()
Equation (B.6), substituted into Eq. (B.2), yields a set of nonlinear algebraic equations, one for each interior node in the finite-difference grid. Two additional equations come from analysis of the boundary conditions. The boundary condition at x = 0 is that of constant flux S0:
[D (δh / δx) ]x=0 = S0. (B.7)
By using the center difference approximation at x = Δx/2 and time step n + 1/2, we obtain
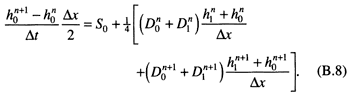
The boundary condition on the right-hand side is maintenance of constant slope between the three end nodes. For m nodes,
![]()
![]()
This set of m nonlinear equations must be solved simultaneously in an iterative fashion to the degree of accuracy desired for all hn+1 values. A numerical root-finding scheme, such as Newton's method (Strang, 1986), solves for the unknown values of hn+1.
We thank P. Flemings, B. Coakley, R. Slingerland, and J. Southard for criticisms, free exchange of ideas, and preprints. This research was supported by the Chevron Oil Field Research Company and the National Science Foundation under grant EAR 89-16870. We also thank J. French, C. Paola, W. Ross, J. Thome, and D. Watts for constructive reviews of the manuscript.
Aigner, T., Doyle, M., Lawrence, D., Epting, M., and Van Vliet, A., 1989, Quantitative modeling of carbonate platforms-some examples; in, Controls on Carbonate Platform and Basin Development, P. D. Crevello, J. L. Wilson, J. F. Sarg, and J. F. Read, ed.: Society of Economic Paleontologists and Mineralogists, Special Publication 44, p. 27-38
Allen, J. R. L., 1985, Principles of physical sedimentation: Allen & Unwin, Ltd., London, 272 p.
Angevine, C. L., 1989, Relationship of eustatic oscillations to regressions and transgressions on passive continental margins; in, Origin and Evolution of Sedimentary Basins and Their Energy and Mineral Resources, R. A. Price, ed.: American Geophysical Union, Washington, DC, p. 29-35
Bally, A., 1987, Atlas of seismic stratigraphy: American Association of Petroleum Geologists, Studies in Geology 27, 127 p.
Begin, Z. B., Meyer, D. F., and Schumm, S. A., 1981, Development of longitudinal profiles of alluvial channels in response to base-level lowering: Earth Surface Processes and Landforms, v. 6, p. 49-68
Bitzer, K., and Harbaugh, J. H., 1987, DEPOSIM--a Macintosh computer model for two-dimensional simulation of transport, deposition, erosion, and compaction of clastic sediments: Computers and Geosciences, v. 13, p. 611-637
Clarke, T. L., Swift, D. J. P., and Young, R. A., 1983, A stochastic modeling approach to shelf sediment dispersal: Journal of Geophysical Research, v. 88, p. 9,653-9,660
Crank, J., 1975, The mathematics of diffusion: Oxford University Press, New York, 414 p.
Culling, W. E. H., 1965, Theory of erosion on soil covered slopes: Journal of Geology, v. 73, p. 230-254
Driver, E. S., and Pardo, G., 1974, Seismic traverse across the Gabon continental margin; in, The Geology of Continental Margins, C. A. Burk and C. L. Drake, eds.: Springer-Verlag, New York, p. 293-296
Dunham, R. J., 1969, Vadose pisolite in the Capitan reef (Permian), New Mexico and Texas; in, Depositional Environments in Carbonate Rocks, G. M. Friedman, ed.: Society of Economic Paleontologists and Mineralogists, Special Publication 14, p. 182-191
Ericksen, M. C., and Slingerland, R., 1990, Numerical simulations of tidal and wind-driven circulation in the Cretaceous Interior Seaway of North America: Geological Society of America, Bulletin, v. 102, p. 1,499-1,516
Ericksen, M. C., Masson, D. S., Slingerland, R., and Swetland, D. W., 1989, Numerical simulation of circulation and sediment transport in the Late Devonian Catskill Sea; in, Quantitative Dynamic Stratigraphy, T. A. Cross, ed.: Prentice Hall, Englewood Cliffs, New Jersey, p. 293-305
Flemings, P. B., and Jordan, T. E., 1989a, Reconstructing sea-level history from the age of stratigraphic sequence boundaries: Geological Society of America, Abstracts with Programs, p. 166167
Flemings, P. B., and Jordan, T. E., 1989b, A synthetic stratigraphic model of foreland basin development: Journal of Geophysical Research, v. 94, no. B4, p. 3,851-3,866
Gildner, R. F., and Cisne, J. L., 1989, Quantitative modeling of carbonate stratigraphy and water-depth history using depth-dependent sediment accumulation function; in, Quantitative Dynamic Stratigraphy, T. A. Cross, ed.: Prentice Hall, Englewood Cliffs, New Jersey, p. 417-432
Goldhammer, R. K., Dunn, P., and Hardie, L. A., 1987, High frequency glacio-eustatic sea-level oscillations with Milankovitch characteristics recorded in Middle Triassic cyclic platform carbonates, northern Italy: American Journal of Science, v. 287, p. 853-892
Grotzinger, J. P., 1986, Cyclicity and paleoenvironmental dynamics, Rocknest platform, northwest Canada: Geological Society of America, Bulletin, v. 97, p. 1,208-1,231
Grow, J. A., Klitgord, K. A., and Schlee, J. S., 1987, Structure and evolution of Baltimore Canyon trough; in, The Decade of North American Geology--The Atlantic Continental Margin, U.S., R. E. Sheridan and J. A. Grow, eds.: Geological Society of America, v. 1-2, p. 269-290
Harbaugh, J. W., 1966, Mathematical simulation of marine sedimentation with IBM 7090/7094 computers: Kansas Geological Survey, Computer Contributions Series 1, 52 p.
Incropera, F. G., and DeWitt, D. P., 1985, Introduction to heat transfer: John Wiley and Sons, New York, 712 p.
Jervey, M. T., 1988, Quantitative geological modeling of siliciclastic rock sequences and their seismic expression; in, Sea-Level Changes--An Integrated Approach, C. K. Wilgus, B. S. Hastings, C. G. St. C. Kendall, H. W. Posamentier, C. A. Ross, and J. C. Van Wagoner, eds.: Society of Economic Paleontologists and Mineralogists, Special Publication 42, p. 47-70
Jordan, T. E., and Flemings, P. B., 1990, From geodynamic models to basin fill--a stratigraphic perspective; in, Quantitative Dynamic Stratigraphy, T. A. Cross, ed.: Prentice Hall, Englewood Cliffs, New Jersey, p. 149-163
Jordan, T. E., and Flemings, P. B., 1991, Large-scale stratigraphic architecture, eustatic variation, and unsteady tectonism--a theoretical evaluation: Journal of Geophysical Research, sec. B, v. 96, p. 6,681-6,699
Kenyon, P. M., and Turcotte, D. L., 1985, Morphology of a prograding delta by bulk sediment transport: Geological Society of America, Bulletin, v. 96, p. 1,457-1,465
Lawrence, D. T., Doyle, M., and Aigner, T., 1990, Stratigraphic simulation of sedimentary basins--concepts and calibration: American Association of Petroleum Geologists, Bulletin, v. 74, p. 273-295
Leckie, D. A., and Krystinik, L. F., 1989, Is there evidence for geostrophic currents preserved in the sedimentary record of inner to middle-shelf deposits?: Journal of Sedimentary Petrology, v. 59, p. 862-870
Leckie, D. A., and Krystinik, L. F., 1991, Is there evidence for geostrophic currents preserved in the sedimentary record of inner- to middle-shelf deposits?--reply: Journal of Sedimentary Petrology, v. 6 1, p. 152-154
Middleton, G. V., and Southard, J. B., 1984, Mechanics of sediment movement: Society of Economic Paleontologist and Mineralogists, Short Course 3, 394 p.
Paola, C., 1990, A simple basin-filling model for coarse-grained alluvial systems; in, Quantitative Dynamic Stratigraphy, T. A. Cross, ed.: Prentice Hall, Englewood Cliffs, New Jersey, p. 363374
Plint, A. G., 1988, Sharp-based shoreface sequences and "offshore bars" in the Cardium Formation of Alberta--their relationship to relative changes in sea level; in, Sea-Level Changes-An Integrated Approach, C. K. Wilgus, B. S. Hastings, C. G. St. C. Kendall, H. W. Posamentier, C. A. Ross, and J. C. Van Wagoner, eds.: Society of Economic Paleontologists and Mineralogists, Special Publication 42, p. 357-370
Press, W. H., Flannery, B. P., Teukolsky, S. A., and Vetterling, W. T., 1986, Numerical recipes--the art of scientific computing: Cambridge University Press, Cambridge, 818 p.
Read, J. F., Grotzinger, J. P., Bova, J. A., and Koerschner, W. F., 1986, Models for generation of carbonate cycles: Geology, v. 14, p. 107-110
Strang, G., 1986, Introduction to applied mathematics: Wellesley-Cambridge Press, Wellesley, Massachusetts, 758 p.
Strobel, J., Soewito, F., Kendall, C. G. St. C., Biswas, G., Bezdek, J., and Cannon, R., 1990, Interactive simulation (SED-PACK) of clastic and carbonate sedimentation in shelf to basin settings; in, Quantitative Dynamic Stratigraphy, T. A. Cross, ed.: Prentice Hall, Englewood Cliffs, New Jersey, p. 433-444
Swift, D. J. P., Thome, J. A., and Oertel, G. F., 1986, Fluid processes and sea-floor response on a modern storm-dominated shelf, middle Atlantic shelf of North America--pt. 2, response of the shelf floor; in, Shelf Sands and Sandstones, R. J. Knight and J. R. McLean, eds.: Canadian Society of Petroleum Geologists, Memoir 11, p. 191-211
Tetzlaff, D. M., and Harbaugh, J. W., 1989, Simulating clastic sedimentation: Van Nostrand Reinhold, New York, 202 p.
Kansas Geological Survey
Comments to webadmin@kgs.ku.edu
Web version April 27, 2010. Original publication date 1991.
URL=http://www.kgs.ku.edu/Publications/Bulletins/233/Kaufman/index.html