Kansas Geological Survey, Bulletin 233, p. 294-317
by
Gerard C. Bond1, Michelle A. Kominz2, and John Beavan1
1Lamont-Doherty Geological Observatory
2University of Texas
We have applied a new method (gamma method) for constructing high-resolution age models to peritidal cycles in the Middle Cambrian Pierson Cove Formation (13 cycles) and the Trippe Limestone (40 cycles) exposed in the Wah Wah range, south-central Utah. Spectral analyses of the time series for the gamma age model indicate the presence of significant spectral peaks (relative to a null model) in both data sets. After experimenting with different assumptions for the duration of the mean primary or measured cycle, we found that for the Trippe data set assigning the mean duration of precession to the mean primary cycle produced a reasonably good correlation between the spectrum and the early Paleozoic estimate of insolation forcing. In particular, the periods of the three significant spectral peaks in the Trippe record correspond to estimated line periods for eccentricity and precession and a combination tone of precession. A spectrum for the Trippe cycles based on the conventional assumption that time is proportional to thickness contained only one significant peak, and reasonable estimates of the duration of the mean primary cycle produced a poor fit to the insolation model. Spectral results from the Pierson Cove cycles were less compelling, possibly because of the short length of the record. The presence in the Trippe spectrum of significant peaks with periods corresponding to high-frequency orbital variations suggests that preservation of high-frequency Milankovitch signals is more common than implied by models of shallow marine cyclicity based on Pleistocene sea-level records. The results of these spectral analyses suggest that the gamma method can be used to construct age models for peritidal carbonate cycles that are accurate enough to test for periodicity and deterministic mechanisms, even in rocks as old as the Cambrian.
An Acrobat PDF file containing the complete paper is available (1.8 MB).
One of the obstacles to documenting orbital forcing of cyclic strata is the lack of a time scale with sufficient resolution (Fischer, 1986; Arthur et al., 1984; Algeo and Wilkinson, 1988; Anders et al., 1987). This problem has been largely overcome in the analyses of Pleistocene and Holocene deep-sea climate cycles, mainly because of the development of orbital-tuning methods [e.g., Imbrie et al. (1984) and Martinson et al. (1987)]. However, these methods become much less reliable for strata older than about 1 Ma because of uncertainties in the amplitude and phase of the different components of the insolation signal that are used to tune and test the time scale (Berger, 1977). Even so, less rigorous tuning methods are producing encouraging evidence of Milankovitch-like periodicities in lake cycles of Triassic to Jurassic age (Olsen, 1986) and deep-sea cycles of Cretaceous age (Park and Herbert, 1987; Herbert and Fischer, 1986; Herbert et al., 1989).
We have recently approached the age model problem in a different way, using a procedure described by Kominz and Bond (1990) that we call the gamma method (gamma is a quantity equal to time per unit thickness of sediment). We applied this technique to cyclic lake sediments of Jurassic age in the Newark Supergroup (Kominz and Bond, 1990; Kominz et al., this volume) and obtained spectra with characteristic Milankovitch periodicities that are similar to those reported previously by Olsen (1986). The spectral peaks produced by the gamma age model are more reliable statistically than those based on the age model used in the previous work, in which age is assumed to be directly proportional to time (Kominz et al., this volume).
Encouraged by the outcome of the work on the Jurassic strata, we have begun developing a gamma age model for a sample from a different and much older succession of cycles. These cycles are composed of subtidal to peritidal carbonate sediments and occur in Middle Cambrian strata in the Wah Wah range of south-central Utah (fig. 1). In this article we describe our initial results from sections measured through two cyclic sequences in these strata, one in the Trippe Limestone and the other in the underlying Pierson Cove Formation (fig. 2). The best data have come from a section through the Trippe Limestone, and the majority of our discussion is focused on that record. Spectral analyses applied to a gamma age model for these cycles suggest that the ratios of spectral peaks are compatible with orbital forcing. Using a null model to test for the statistical significance of the spectral peaks and to eliminate circularity in interpreting the data, we found that spectral peaks with periodicities corresponding to the precessional index and the short eccentricity cycles are statistically significant and not forced by the methodology. An especially intriguing result is that the spectral peak ratios seem to correspond more closely to those recently calculated for early Paleozoic time [e.g. Berger et al. (1989)] than for the modern. The Pierson Cove data set produced less convincing evidence of Milankovitch-like periodicity, and we only briefly compare the results of this record with those from the Trippe Limestone.
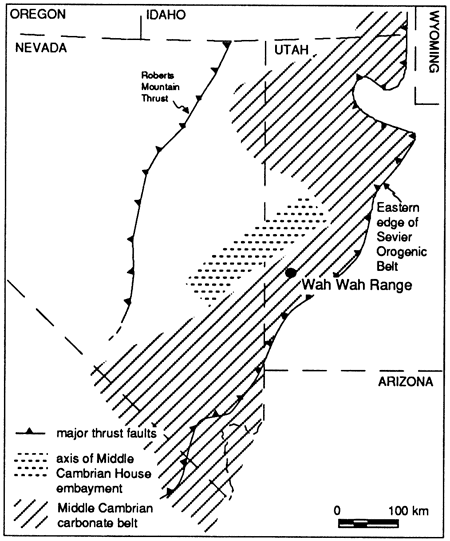
Figure 1--Location of the Wah Wah range, Utah, where the sections of cyclic strata in the Trippe Limestone and the Pierson Cove Formation were measured, and location of the Middle Cambrian House embayment and the Middle Cambrian carbonate belt [from Palmer (1971)].

The Middle Cambrian peritidal cycles that we have analyzed in the Wah Wah range lie within the extensive middle carbonate belt of Palmer (1971), a northeast-trending carbonate shoal complex over 100 km (60 mi) wide in central Utah (fig. 1). The cyclic sequences are from a continuous interval through a part of this shoal, comprising the upper part of the Pierson Cove Formation and most of the overlying Trippe Limestone (fig. 2). In addition to well-developed cyclic sequences, these strata have relatively high accumulation rates resulting from rapid thermal collapse in the middle to outer parts of the early Paleozoic passive margin of western North America (Bond et al., 1983, 1989). Rapid subsidence is especially important to our analyses because it "stretches" the cyclic record, thereby reducing the potential for erosion during sea-level falls and increasing the chances of recording high-frequency (precessional) components of the forcing signal, which are commonly missing in more slowly subsiding settings [e.g., Grotzinger (1986), Read et al. (1986), and Goldhammer et al. (1990)].
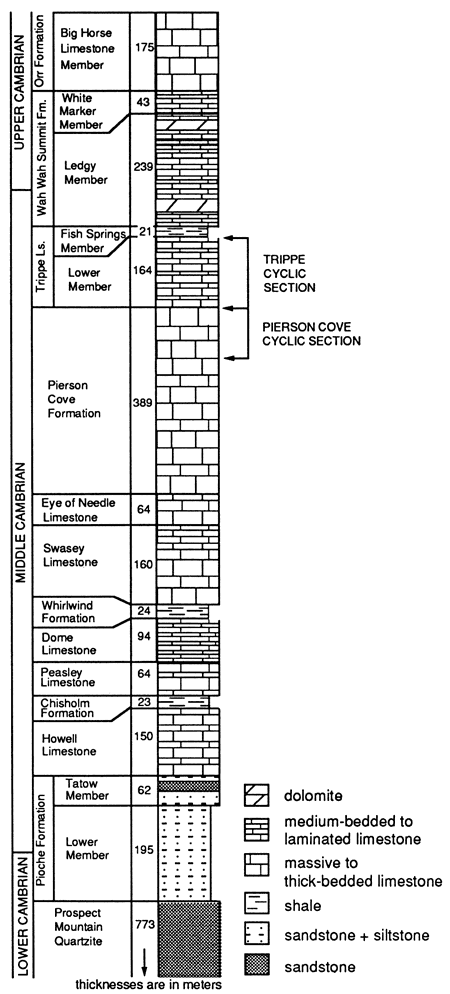
Figure 2--Generalized stratigraphic column for Cambrian strata in the Wah Wah range, Utah. Arrows mark the stratigraphic position of the measured sections through cyclic strata in the Trippe Limestone and the Pierson Cove Formation [from Wheeler (1980)].
The carbonate shoal was flanked on the west by a relatively deep-water trough, the House embayment (fig. 1). The trough has been interpreted as a Middle Cambrian structural basin formed by faulting along its eastern edge (fig. 1) (Kepper, 1976, 1981; Brady and Koepnick, 1979; Rees, 1986). If the structural model is correct, contemporaneous faulting could have influenced the cyclicity in our sample. As we discuss in a subsequent section, however, the effect of faulting, if it occurred, is most likely random and distinct from the periodicities we observe in the spectral data.
The Trippe Limestone consists of a thick, informally defined lower member overlain by the thin but regionally extensive Fish Springs Member (fig. 2) (Hintze and Robison, 1975). The lower member, which contains the cyclic section that we measured, has a striking meter-scale light-dark banding that is easily recognized, even from a distance. These bands are produced by an interbedding of cream-colored dolomitic cryptalgalaminates with dark-gray mottled limestone and gray oolitic grainstone. The Fish Springs Member contains interbedded shale and intraformational conglomerate with a well-documented Eldoradia fauna (Hintze and Robison, 1975). The Trippe Limestone has been mapped throughout much of western Utah and eastern Nevada, and its identification has been facilitated by these two distinctive members. The distinct cyclicity of the lower member has been described previously, particularly by Kepper (1972, 1976). He identified a repetition of facies formed in environments ranging from shallow subtidal basins (mottled limestones) to high-energy bars (grainstones) and algal mat-covered tidal mudbanks (cream-colored boundstone or cryptalgalaminates).
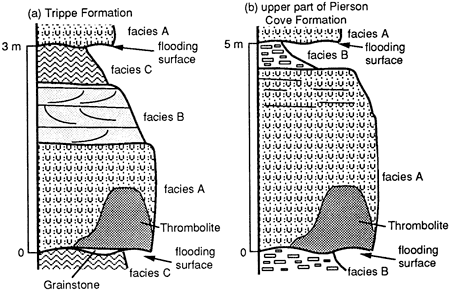
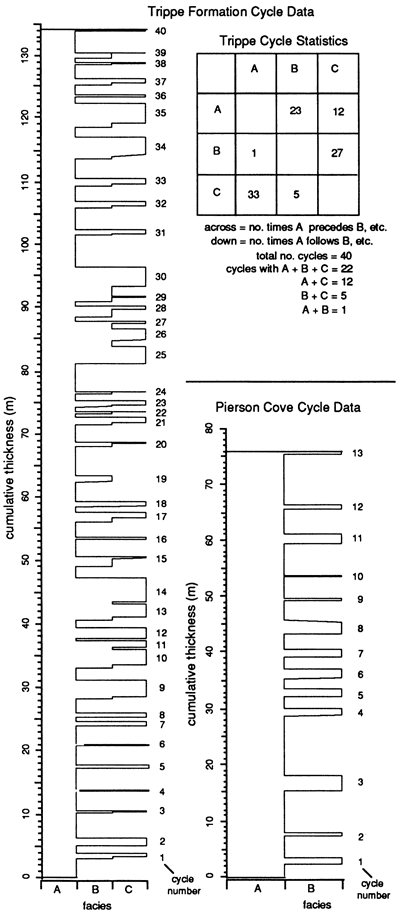
We have measured a section 134 m (440 ft) thick through the carbonate shoal deposits in the lower member of the Trippe Limestone on the western flank of the northern portion of the Wah Wah range approximately 5 mi (8 km) north of Utah State Highway 21. The section begins with the first cycle capped with cream-colored cryptalgalaminate at the transitional contact with the underlying Pierson Cove Formation and ends with the last cycle capped by cryptalgalaminate, which lies approximately 30 m (100 ft) below the Fish Springs Member. The section contains the tidal to subtidal facies identified by Kepper (1972), arranged in 40 distinct cycles, averaging 3.25 m (11 ft) thick (table 1). Each cycle begins with a massive, pervasively burrowmottled lime mudstone-siltstone, designated facies A (fig. 3). It has an average thickness of 1.9 m (6.2 ft) (table 1). Discontinuous layers of thrombolites are common in this facies. In a few of the cycles facies A is underlain by thin, discontinuous lenses of medium- to fine-grained grainstone.
In the most frequently occurring type of cycle, facies A is followed by two distinctly different facies (figs. 3 and 4). The first, facies B, is a medium-grained, mostly oolitic grainstone that is crossbedded, largely unburrowed, and generally between 0.3 and 0.5 m (1-1.6 ft) thick. The contact between the two facies commonly is erosional. The uppermost facies, facies C, is a distinctive, cream-colored layer of mostly dolomitized cryptalgalaminate averaging 1 m (3 ft) thick. It commonly contains a few mudcrack structures, thin, discontinuous layers of grainstone, thin interbeds of gray peloidal laminated limestone, scattered columnar stromatolites, angular rip-up clasts of the dolomitized laminites, and, in a few cycles, teepee structures. This facies is separated from facies B below and from the next cycle above by erosional surfaces. Rip-up clasts of the laminite commonly are scattered through the lower part of the overlying facies A. The A to B to C cycle pattern strongly resembles the shoaling-upward cycles with shallow tidal to intertidal caps that are common in modern and ancient peritidal cyclic sequences [e.g., James (1984) and Shinn (1983)]. Two subordinate types of cycles also are present, one consisting of only facies B followed by facies C and the other consisting of facies A followed by facies C (fig. 4). The lithologic characteristics of facies A, B, and C do not change from the dominant cycle type through these two subordinate types.
Table 1--Cycle data from Pierson Cove and Trippe Formations
| Datum | Pierson Cove Formationa | Trippe Limestoneb |
|---|---|---|
| Measured thickness (m) | 70 | 134 |
| Number and thickness (m) of noncyclic intervals |
0 | 0 |
| Number and thickness (m) of covered intervals |
0 | 1,4.0 |
| Total number of measured cycles |
13 | 40 |
| Average cycle thickness (m) ± standard deviation |
5.39 ± 2.67 | 3.25 ± 2.41* |
| Average facies thickness (m) | Facies Ac: 4.44 ± 2.73 | Facies Ac: 1.86 ± 1.54 |
| Facies Bd: 0.95 ± 0.55 | Facies Be: 0.42 ± 0.40 | |
| Facies Cf: 0.97 ± 1.05 | ||
| a. Wah Wah Summit quadrangle, NW NW sec. 26, T. 25 S., R. 16 W. b. Wah Wah Summit quadrangle, SSE sec. 26, T. 25 S., R. 16 W. c. Massive lime mud + thrombolite. d. Nodular muddy limestone. e. Grainstone. f. Laminite. *Note that, because there are 4 m of covered interval, the mean cycle thickness is not given by 134 m ÷ 40 cycles. It is calculated from the measured thicknesses of the 40 cycles. |
||
Figure 3--Typical occurrence of facies in meter-scale peritidal cycles from the upper part of the Pierson Cove Formation and in the Trippe Limestone. See text for description of lithologies in the facies in the cycles.
Fortunately, the regularity of the facies successions makes the cyclicity quite evident in the Trippe Limestone. The three facies occur in only three repeating patterns that are easily recognized (figs. 3 and 4), and it is unnecessary to apply statistical methods to test for cyclicity using Markov chain or substitutability analyses (Davis, 1973). The ease in recognizing the cyclic pattern directly in the field and the simplicity of the pattern were, in fact, important criteria in selecting these strata for analysis.
Figure 4--Vertical distribution of facies in the cyclic sections of the Trippe Limestone and the Pierson Cove Formation. Note the dominance of the pattern ABC in the Trippe section. Cycles composed of facies A and C, B and C, and A and B also occur but are much less common. The box at the right emphasizes the predominance of ABC cycles in the Trippe section by showing how often facies B follows facies A, C follows B, etc.
The Pierson Cove Formation was defined by Hintze and Robison (1975) to include a thick sequence of dark-gray limestones and dolomites below the Trippe Limestone and above the light-gray massive limestones of the Eye of Needle Limestone (fig. 2). Hintze and Robison recognized three dominant lithologies in the formation: a dark-gray mottled lime mudstone; a massive finely crystalline, medium-gray limestone; and a yellowish-gray laminated, dolomitic boundstone. The first two rock types probably are subtidal deposits. The third type was probably deposited in a tidal to intertidal environment. The contact with the overlying Trippe Limestone is gradational over a few meters. It is characterized mainly by a gradual replacement of the yellowish-gray boundstone of the Pierson Cove Formation by the cream-colored dolomitized laminite of the Trippe Limestone.
The section through the Pierson Cove Formation was measured in the upper fourth of the formation (fig. 2) where it is exposed on the western flank of the northern part of the Wah Wah range, approximately 5 mi (8 km) north of Utah State Highway 21. The section lies less than 1 km (0.6 mi) south of the location of the Trippe section. The base of the section is at the first occurrence of the repeating facies pattern in the upper part of the formation. The top of the section is at the base of the first cycle capped with the cream-colored cryptalgalaminate in the Trippe Limestone. This first Trippe cycle is laterally continuous with the first cycle in the Trippe data set, providing an accurate correlation of strata between the two locations. The Pierson Cove section is 70 m (230 ft) thick and contains 13 cycles, averaging 5.4 m (18 ft) thick (table 1).
Each Pierson Cove cycle consists of two facies. The lower facies begins with a massive, pervasively burrow-mottled lime mudstone-siltstone, designated facies A, with an average thickness of 4-5 m (12-16 ft) (fig. 3; table 1). The mottling is tan and dolomitized. Discontinuous layers of thrombolites occur in this facies in several of the cycles. The uppermost part of this facies is a thin- to medium-bedded lime mudstone-siltstone with less pervasive dolomitized mottling and discontinuous thin lenses of packstone and/or grainstone. This facies includes the mottled lime mudstone and fine crystalline limestone lithologies described by Hintze and Robison (1975). The facies probably formed in a quiet-water subtidal environment.
The upper Pierson Cove facies, facies B, is a distinctive nodular limestone averaging a little less than 1 m (3 ft) in thickness, and in most of the cycles it is in gradational contact with facies A over a few centimeters. The nodules are limy, have centimeter-scale lengths and thicknesses, and occur in a tan dolomitized matrix. Many of the nodules have polygonal shapes in bedding plane surfaces, suggesting mudcracks, and some have millimeter- scale internal laminations. This facies is equivalent to the yellowish-gray boundstone described by Hintze and Robison (1975). The facies strongly resembles deposits recognized by Kepper (1976) in Middle Cambrian strata of the Great basin and by Matter (1967) in the Ordovician strata of the Appalachians; these deposits were interpreted as the remnants of algal mats formed in tidal flats. The facies is distinctive in the near absence of the cream-colored dolomitization that characterizes the tops of many other peritidal cyclic sequences in the Great basin [e.g., Halley (1974), Kepper (1972, 1976), and Brady and Koepnick (1979)]. The absence of this distinct dolomitization may reflect a relatively short time of subaerial exposure and desiccation of the cycle tops. Commonly, facies B is terminated by an abrupt irregular boundary that is probably a flooding surface (fig. 3). In some of the cycles, however, facies B grades into facies A of the next cycle over an interval of a few centimeters, suggesting that at least some of the cycle tops were not eroded.
As is the case for the Trippe cycles, the cyclicity of the Pierson Cove cycles is straightforward. This is due to the simple repeating pattern of two distinctly different facies that characterizes the Pierson Cove strata (figs. 3 and 4).
The gamma method produces an age model by obtaining an approximate solution to the relation between time and facies in a succession of sedimentary cycles. We have modified the procedure for constructing the age model described by Kominz and Bond (1990) to incorporate two improvements. We now use a least-squares method to calculate gamma values (values of time per unit thickness for individual lithologies) so that all the data are included instead of only the positive results, as before. In addition, we developed a null model to evaluate the statistical significance of spectral peaks observed in the Fourier results.
The gamma method approaches the problem of correcting for variations in time per unit thickness through a cyclic data set by first specifying two ideal conditions: (1) If, within essentially the same general depositional environment, a succession of cycles has a repeating pattern of facies, the time per unit thickness is essentially constant for each facies. The value of that constant may be (and probably is) different for each facies. (2) The durations of the cycles vary by relatively small amounts.
We recognize that neither condition will necessarily be met in a given succession of cycles. As will become apparent in what follows, if the two conditions are not met in a succession of cycles, the least-squares inversion procedure will fail to produce a solution or the gamma method will fail to produce a time series with statistically significant periodicities. In fact, we have found that the gamma method produces a spectrum with statistically significant peaks in a little more than one out of every two attempts. We emphasize that specifying the two conditions does not force the procedure to work.
If the cycles do come close to satisfying both conditions, then the differences in cycle thicknesses must be due primarily to differences in the length of accumulation of each facies coupled with the differences in the effective accumulation rates of the different facies. We use the term "effective accumulation rate" to indicate the thickness (as observed today) per unit time. It includes the effects of changes in sedimentation rates, compaction, dissolution, nondeposition, erosion, etc. from one facies to the next. The effective accumulation rate should be thought of as a relative rate because we do not attempt to specify the absolute duration of a cycle or of a facies.
Next, we consider a hypothetical situation in which all the observed cycles have exactly the same duration (Tcy = a constant) and in which the gamma values for each facies are exactly the same. Although this situation probably never exists in nature, it allows us to establish a mathematical basis for the gamma procedure. For a given facies i we define the assumed proportional relationship between facies thickness and time as Ti = γiCi, where Ti equals time, Ci equals thickness, and γi is the proportionality constant (fig. 5). For a cycle with n facies, the cycle duration Tcy, is related to its thickness by
![]()
Figure 5--Illustration of the gamma method--estimating the ages of facies of a single, arbitrary cycle A composed of four facies [from Kominz and Bond (1990)]. In the example, each of the four facies is indicated by a pattern. (a) The conventional assumption that the observed sediment thickness is proportional to age, independent of facies. In this case a single factor, γ, which is the time per unit thickness, is used to estimate the age within the cycle. (b) The assumption that each facies has a specific relation between time and thickness, given by the value γ. The slopes, or γi, are arbitrary in this example. The actual values of γi are calculated by applying the gamma method described in the text.
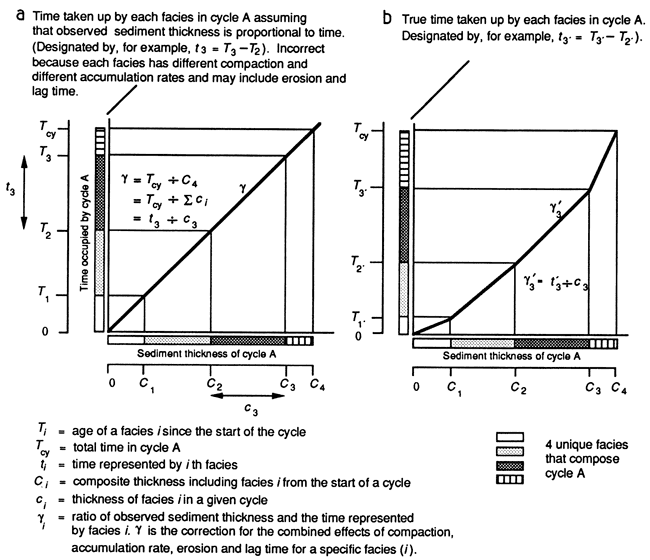
So far we have described ideal conditions that are unlikely to exist in nature; can we make Eq. (1) work in a succession of real cycles? The key to answering that question is in the observation that commonly there are many more cycles (m) than facies (n); thus there are many more equations than unknown γi. This is an overdetermined set of equations, and the additional information in the extra equations allows us to obtain at least approximate solutions to Eq. (1). To do this, we solve the overdetermined set of equations by a standard least-squares inversion. [This is a refinement of the procedure we used earlier (Kominz and Bond, 1990) for the same step.] Because γi cannot be less than 0 (i.e., no facies can have negative thickness), we solve the equations subject to the constraint that the unknowns are greater than 0. This is the well-known "positive least-squares" inversion [e.g., Lawson and Hanson (1974) and Menke (1984)]. Some of the cycles within a data set may be outliers; that is, an unusually thick cycle may actually be two or more cycles amalgamated by erosion or nondeposition of entire facies, or facies in unusually thin cycles may have lost substantial material by erosion. Consequently, we add a refinement to the procedure. After the first inversion, we remove the worst-fitting cycle (i.e., the one with the largest residual) from the data set and repeat the inversion, calculating the error each time (see definition of "error" in tables 2 and 3). The resulting γi for each of these iterations are put back into the total cycle data set, and the error is calculated (see definition of "error total" in tables 2 and 3). By examining how much the γi change with each iteration, we obtain an estimate of their stability. We emphasize also that the iteration process does not remove thin or thick cycles exclusively; hence there is no bias in this procedure toward thinner or thicker cycles.
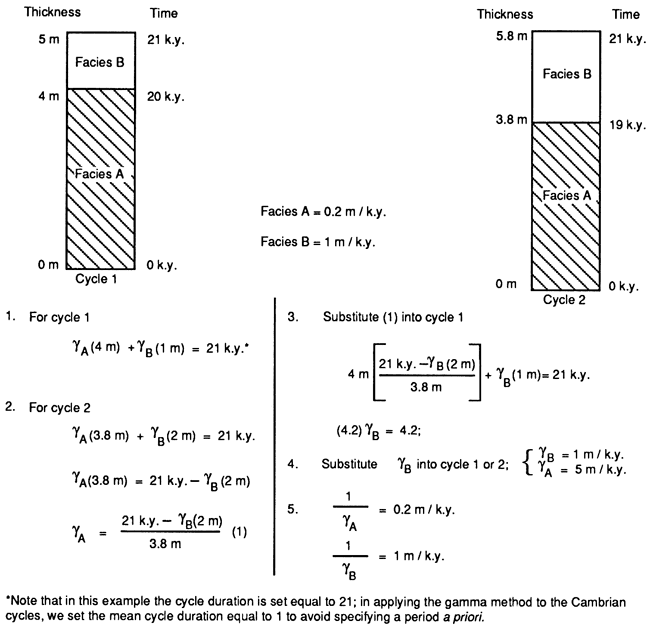
Figure 6--An example of the calculation of the γi for the simple case of two cycles and two facies. Note that in this example the thickest facies is the slowest accumulating facies.
If the γi are relatively stable, we proceed to the next step, which is to determine whether or not periodic components are present in the cyclic record. We first convert the depth series of the cyclic sequence to a relative time series by multiplying the thickness of each facies by the appropriate γi, which is in units of time per unit thickness. The relative time series is then tested for periodicity using methods of spectral analysis. To avoid specifying the duration of the primary (measured) cycle in this step, we set its mean equal to unity. If statistically significant spectral peaks are present, we can recalculate the periodicities by altering the mean duration of the primary cycle. It is then possible to test the degree to which these other periodicities correspond to different models of periodic processes, in particular, the orbital or Milankovitch model. It is possible that no spectral peaks will be found or that the tuning procedure will fail to produce any correspondence between observed spectral peaks and the Milankovitch model. In the latter case, we can conclude that the cycles are periodic, but it would be difficult to identify the periodic forcing mechanism. As discussed later, we avoid circular reasoning that could arise from the assumptions built into the procedure by comparing the spectral data with an appropriate null model.
Following the procedure described, we calculated gamma values for the cycles in the Pierson Cove and Trippe sections. For the Pierson Cove section we calculated γi for all cycles together (table 2). We calculated γi for the Trippe section in two ways, one for all cycles combined (table 2) and the other for each of the three cycle categories separately (that is, A + B + C only, B + C only, and A + C only; table 3). Note that γi is calculated assuming that the duration of the mean primary cycle (the mean measured cycle) is equal to 1. The total error for all groupings of cycles, as defined in tables 2 and 3, is relatively large but varies little through the iterations. The large error is not surprising, given the potential for erosion of cycle tops and amalgamation of cycles together with the fact that forcing at the eccentricity and precessional frequencies, if that is the origin of the cycles, does not produce cycles of constant duration [see for example, Berger et al. (1988), summarized in fig. 12a]. We do not regard the large error by itself to be a sufficient basis for rejecting the cyclic section.
How much γi should vary in a natural system is extremely difficult to assess because of the complexity of sediment-ocean systems and their interaction with stochastic or deterministic mechanisms. Values of γi probably will always be unstable to a degree because the cycles do not perfectly match our initial conditions. With this in mind we prefer to select γi from the first few iterations, provided that they tend to be relatively stable or constant through those iterations. This is because the values from low numbers of iterations are closest to the mean of the total range of li values in the data set. If we select values after many iterations, even though they may fall within a stable region, we are throwing out data and choosing values from only one component of the mean.
For the Pierson Cove cycles the most stable least-squares results are between iterations 3 and 6 (table 2), and we selected the γi values from iteration 5. In the Trippe least-squares solution for all cycles combined, the y values for facies A and B are reasonably stable for all iterations; we chose values at the first plateau for facies B, which occurs after only six iterations (table 2). For the alternative grouping of facies, the A + B + C data set yields stable values for facies A and C similar to those for all cycles, but facies B is not stable until over half the cycles are removed. We prefer then to use the γi values at the low iteration numbers, even though the values for facies B are still falling. For the other two groupings (A + C and B + C) there are so few cycles that we chose values from the first iteration. We are not surprised at the difference in the values for facies C in the A + C grouping, given the few number of A + C cycles. In fact, we are encouraged by the overall similarity of γi in the selections we made from the Trippe data sets in both tables. The γi values have broadly the same relation to each other; values for facies B are always the largest, and values for facies A are always slightly larger than the values for facies C. We regard this as an acceptable degree of stability of γi. We note, however, that the gamma values probably are more reliable (or stable) for the first grouping (table 2). Thus the Pierson Cove and Trippe data sets have passed the first test; that is, they contain what seem to be reasonably stable gamma values.
Table 2--Gamma data for Trippe and Pierson Cove cycles
| Iteration | γA | γB | γC | Errora | Error Totalb |
Average Timec |
Time Totald |
|---|---|---|---|---|---|---|---|
| Trippe (all cycles) | |||||||
| 1 | 0.210 | 0.620 | 0.177 | 0.419 | 0.419 | 0.824 | 0.824 |
| 2 | 0.206 | 0.625 | 0.179 | 0.403 | 0.419 | 0.838 | 0.821 |
| 3 | 0.206 | 0.640 | 0.168 | 0.385 | 0.419 | 0.852 | 0.817 |
| 4 | 0.204 | 0.654 | 0.161 | 0.368 | 0.420 | 0.864 | 0.813 |
| 5 | 0.201 | 0.668 | 0.155 | 0.353 | 0.421 | 0.876 | 0.808 |
| 6 | 0.195 | 0.676 | 0.158 | 0.337 | 0.421 | 0.886 | 0.802 |
| 7 | 0.195 | 0.652 | 0.162 | 0.323 | 0.421 | 0.896 | 0.797 |
| 8 | 0.196 | 0.681 | 0.141 | 0.306 | 0.423 | 0.907 | 0.790 |
| 9 | 0.199 | 0.665 | 0.135 | 0.292 | 0.423 | 0.915 | 0.784 |
| 10 | 0.197 | 0.692 | 0.120 | 0.276 | 0.426 | 0.924 | 0.776 |
| 11 | 0.195 | 0.669 | 0.127 | 0.263 | 0.426 | 0.931 | 0.770 |
| 12 | 0.196 | 0.653 | 0.126 | 0.247 | 0.427 | 0.939 | 0.763 |
| 13 | 0.199 | 0.607 | 0.133 | 0.234 | 0.427 | 0.945 | 0.756 |
| 14 | 0.199 | 0.574 | 0.140 | 0.220 | 0.428 | 0.951 | 0.749 |
| 15 | 0.201 | 0.522 | 0.150 | 0.209 | 0.430 | 0.956 | 0.741 |
| 16 | 0.200 | 0.502 | 0.154 | 0.199 | 0.432 | 0.961 | 0.734 |
| 17 | 0.195 | 0.497 | 0.156 | 0.187 | 0.434 | 0.965 | 0.727 |
| 18 | 0.190 | 0.500 | 0.158 | 0.175 | 0.435 | 0.970 | 0.719 |
| 19 | 0.184 | 0.518 | 0.154 | 0.162 | 0.437 | 0.974 | 0.713 |
| 20 | 0.188 | 0.497 | 0.173 | 0.148 | 0.433 | 0.978 | 0.728 |
| 21 | 0.180 | 0.551 | 0.181 | 0.134 | 0.429 | 0.982 | 0.745 |
| 22 | 0.187 | 0.572 | 0.173 | 0.123 | 0.426 | 0.985 | 0.758 |
| 23 | 0.196 | 0.561 | 0.171 | 0.114 | 0.424 | 0.987 | 0.770 |
| 24 | 0.194 | 0.555 | 0.172 | 0.109 | 0.425 | 0.988 | 0.763 |
| 25 | 0.198 | 0.529 | 0.168 | 0.104 | 0.426 | 0.989 | 0.756 |
| 26 | 0.198 | 0.526 | 0.162 | 0.098 | 0.428 | 0.990 | 0.748 |
| 27 | 0.201 | 0.471 | 0.168 | 0.089 | 0.432 | 0.992 | 0.737 |
| 28 | 0.198 | 0.464 | 0.169 | 0.083 | 0.434 | 0.993 | 0.730 |
| 29 | 0.195 | 0.457 | 0.169 | 0.073 | 0.436 | 0.995 | 0.722 |
| 30 | 0.201 | 0.455 | 0.148 | 0.057 | 0.440 | 0.997 | 0.711 |
| 31 | 0.197 | 0.465 | 0.147 | 0.048 | 0.441 | 0.998 | 0.706 |
| 32 | 0.191 | 0.467 | 0.150 | 0.034 | 0.442 | 0.999 | 0.700 |
| 33 | 0.190 | 0.452 | 0.151 | 0.014 | 0.445 | 1.000 | 0.692 |
| 34 | 0.191 | 0.462 | 0.148 | 0.010 | 0.444 | 1.000 | 0.696 |
| 35 | 0.191 | 0.468 | 0.145 | 0.006 | 0.444 | 1.000 | 0.694 |
| 36 | 0.190 | 0.469 | 0.143 | 0.001 | 0.445 | 1.000 | 0.693 |
| 37 | 0.190 | 0.469 | 0.143 | 0.000 | 0.445 | 1.000 | 0.693 |
| 38 | 0.190 | 0.469 | 0.143 | 0.000 | 0.445 | 1.000 | 0.693 |
| Pierson Cove (all cycles) | |||||||
| 1 | 0.11 | 0.6 | 0.329 | 0.329 | 0.895 | 0.895 | |
| 2 | 0.095 | 0.652 | 0.271 | 0.329 | 0.929 | 0.881 | |
| 3 | 0.086 | 0.686 | 0.243 | 0.333 | 0.943 | 0.857 | |
| 4 | 0.081 | 0.705 | 0.219 | 0.338 | 0.952 | 0.838 | |
| 5 | 0.081 | 0.662 | 0.205 | 0.338 | 0.957 | 0.824 | |
| 6 | 0.086 | 0.619 | 0.19 | 0.343 | 0.962 | 0.805 | |
| 7 | 0.086 | 0.576 | 0.162 | 0.348 | 0.971 | 0.781 | |
| 8 | 0.086 | 0.543 | 0.129 | 0.357 | 0.981 | 0.757 | |
| 9 | 0.095 | 0.452 | 0.09 | 0.367 | 0.990 | 0.733 | |
| 10 | 0.1 | 0.386 | 0.048 | 0.386 | 1.000 | 0.705 | |
| 11 | 0.095 | 0.4 | 0.033 | 0.39 | 1.000 | 0.695 | |
| 12 | 0.1 | 0.4 | 0.01 | 0.381 | 1.000 | 0.710 | |
| Boldface values are the gamma values used to construct the age model. a. The root mean square difference between cycle lengths calculated using these values of 7 and the assumed cycle length (= 1). The worst-fitting cycle is removed in each successive iteration, so the error monotonically decreases. b. The same as Error except applied to all cycles in the sequence. c. Mean of cycle lengths for each successive iteration with the worst-fitting cycle removed in each successive iteration. d. The same as Average Time except applied to all the cycles in the sequence. |
|||||||
Because γ is in units of time per thickness, the time scale is constructed by multiplying the measured thickness of each facies by the appropriate γi (fig. 7). Following the procedure developed by Olsen (1986), we assigned a rank number to the facies so that facies A = 1, facies B = 2, and facies C = 3. The y axis or amplitude of the time series is then set equal to the rank numbers. Thus the amplitude variation of the time series approximates the changes in the depositional environment. We square the facies boundaries in the time series because our measurements are taken over the entire facies and the change from one facies to the next is relatively abrupt.
If the cycles were perfectly consistent with the two conditions on which the gamma model is based, as described earlier, the Error and Error Total in tables 2 and 3 would. always be 0 and the Average Time and Time Total would always be unity. This is clearly not true for either of our data sets and to varying degrees probably would not be true for most, if not all, sedimentary cycles. The mean cycle duration is always less than unity for both the Trippe and Pierson Cove cycles (tables 2 and 3), probably because the cycle thicknesses and therefore the cycle durations are bimodal. In the Trippe Limestone the bimodality is mainly due to the tendency for the cycles composed of only two facies to be thinner than the mean thickness of all the cycles. In the Pierson Cove data set the bimodality is due to the presence of a few outliers in which facies A is unusually thick. These may have been produced by unusually high sedimentation rates, or the cycles may actually be composed of more than one cycle in which facies B was eroded or not deposited. We plan to test these alternatives with future fieldwork.
Table 3--Gamma data for alternative grouping of Trippe cycles
| Iteration | γA | γB | γC | Errora | Error Totalb |
Average Timec |
Time Totald |
|---|---|---|---|---|---|---|---|
| Trippe (cycles containing facies A, B, and C) | |||||||
| 1 | 0.195 | 0.79 | 0.1 | 0.3 | 0.3 | 0.910 | 0.910 |
| 2 | 0.195 | 0.752 | 0.105 | 0.276 | 0.3 | 0.924 | 0.900 |
| 3 | 0.2 | 0.724 | 0.1 | 0.257 | 0.3 | 0.933 | 0.890 |
| 4 | 0.195 | 0.695 | 0.11 | 0.238 | 0.305 | 0.943 | 0.876 |
| 5 | 0.2 | 0.648 | 0.114 | 0.224 | 0.305 | 0.952 | 0.867 |
| 6 | 0.219 | 0.671 | 0.09 | 0.205 | 0.305 | 0.957 | 0.895 |
| 7 | 0.257 | 0.633 | 0.062 | 0.186 | 0.319 | 0.967 | 0.933 |
| 8 | 0.262 | 0.562 | 0.067 | 0.167 | 0.329 | 0.971 | 0.919 |
| 9 | 0.267 | 0.543 | 0.095 | 0.148 | 0.333 | 0.976 | 0.943 |
| 10 | 0.262 | 0.514 | 0.1 | 0.129 | 0.333 | 0.986 | 0.929 |
| 11 | 0.252 | 0.519 | 0.11 | 0.114 | 0.329 | 0.986 | 0.914 |
| 12 | 0.233 | 0.533 | 0.124 | 0.095 | 0.324 | 0.990 | 0.895 |
| 13 | 0.243 | 0.524 | 0.105 | 0.081 | 0.324 | 0.995 | 0.890 |
| 14 | 0.248 | 0.457 | 0.11 | 0.062 | 0.338 | 0.995 | 0.876 |
| 15 | 0.243 | 0.448 | 0.114 | 0.043 | 0.338 | 1.000 | 0.862 |
| 16 | 0.238 | 0.448 | 0.119 | 0.038 | 0.338 | 1.000 | 0.852 |
| 17 | 0.229 | 0.443 | 0.124 | 0.019 | 0.338 | 1.000 | 0.843 |
| 18 | 0.229 | 0.438 | 0.124 | 0.019 | 0.338 | 1.000 | 0.838 |
| 19 | 0.233 | 0.433 | 0.119 | 0.014 | 0.338 | 1.000 | 0.838 |
| 20 | 0.229 | 0.438 | 0.119 | 0.005 | 0.338 | 1.000 | 0.829 |
| 21 | 0.229 | 0.433 | 0.124 | 0 | 0.338 | 1.000 | 0.833 |
| 22 | 0.229 | 0.433 | 0.119 | 0 | 0.338 | 1.000 | 0.833 |
| Trippe (cycles containing facies B and C) | |||||||
| 1 | 0.71 | 0.133 | 0.395 | 0.395 | 0.845 | 0.845 | |
| 2 | 0.666 | 0.126 | 0.319 | 0.395 | 0.897 | 0.795 | |
| 3 | 0.347 | 0.218 | 0.186 | 0.443 | 0.966 | 0.715 | |
| Trippe (cycles containing facies A and C) | |||||||
| 1 | 0.196 | 0.759 | 0.357 | 0.357 | 0.873 | 0.873 | |
| 2 | 0.181 | 0.727 | 0.319 | 0.362 | 0.899 | 0.829 | |
| 3 | 0.142 | 0.717 | 0.257 | 0.371 | 0.934 | 0.779 | |
| 4 | 0.184 | 0.603 | 0.005 | 0.39 | 1.000 | 0.723 | |
| Boldface values are the γi used to construct the age model. a. Root mean square difference between cycle lengths calculated using these values of yand the assumed cycle length (= 1). The worst-fitting cycle is removed in each successive iteration, so the error monotonically decreases. b. The same as Error except applied to all cycles in the sequence. c. Mean of cycle lengths for each successive iteration with the worst-fitting cycle removed in each successive iteration. d. The same as Average Time except applied to all the cycles in the sequence. |
|||||||
To adjust for the difference in the gamma-scaled cycle duration and the assumed value of unity, we rescaled the time series to the proper length, which is 40 for the 40 cycles in the Trippe data set and 13 for the cycles in the Pierson Cove formation (fig. 7). If the duration of the time series determined directly by the γi was used instead for the time series, it would be necessary to correct for the shortfalls in cycle durations when calculating the periodicities in the spectral results. This would produce the same value for the periodicities of spectral peaks that we obtain by rescaling the time series and would be a more time-consuming procedure.
It is useful to construct a second time series based on the conventional thickness age model to determine how much the gamma and conventional age models differ. This was done by rescaling the measured section for the cycles to a total length of 40 for the Trippe cycles and 13 for the Pierson Cove cycles. As in the gamma age model, the amplitude is set equal to the rank number (fig. 7).
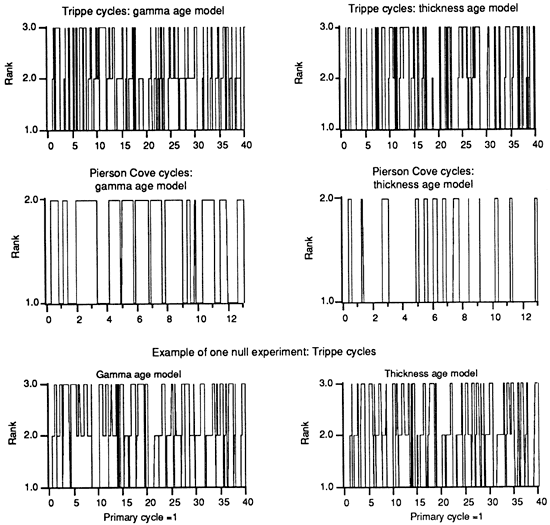
Figure 7--Time series of rank for the Trippe and Pierson Cove cycles calculated by assuming the gamma age model (time Is proportioned by gamma) (left-hand side) and by assuming the thickness age model (time is directly proportional to thickness over the section) (right-hand side). The bottom pair of time series are from one example of ournull hypothesis experiment forthe Trippe cycles, as described in the text. In these plots the mean cycle duration has been set equal to 1. Hence the Trippe series runs from 0 to 40, indicating that 40 cycles are present, and the Pierson Cove data run from 0 to 13. Individual cycle lengths vary somewhat from 1, perhaps indicating variations in astronomical forcing (see fig. 12a) and noise (erosion, amalgamation of cycles, etc.) within the data. The mean cycle duration is referred to as the mean primary cycle in figs. 8 through 15.
We used two procedures for spectral analysis. One is the SPECMAP method (Imbrie et al., 1984) used in Pleistocene climate studies. The other is the multitaper method of Thompson (1982). The SPECMAP method uses the Blackman-Tukey procedure with a Hamming window, whereas the multitaper technique operates directly on the original time series (rather than on its autocovariance function) and uses multiple windowing with prolate spheroidal windows for optimal statistical reliability. We use the SPECMAP method mainly to compare the spectra from the Cambrian cycles directly with spectra from Pleistocene climate records. In addition, the variance probably is underestimated by the SPECMAP method and overestimated by the jackknifing procedure used in the multitaper method, so the two techniques may bracket the true variance.
When using Fourier spectral analysis to study time series with square wave characteristics, such as those in fig. 7, it is necessary to be certain that overtones of the square wave pattern are not interpreted as spectral peaks in their own right [see Weedon (1989)]. We have examined the spectra of numerous artificially generated time series with characteristics similar to the observed data and have found in all cases that the power in the overtones falls off several times more rapidly than the power in the observed peaks from the Trippe and Pierson Cove sections (see later discussion).
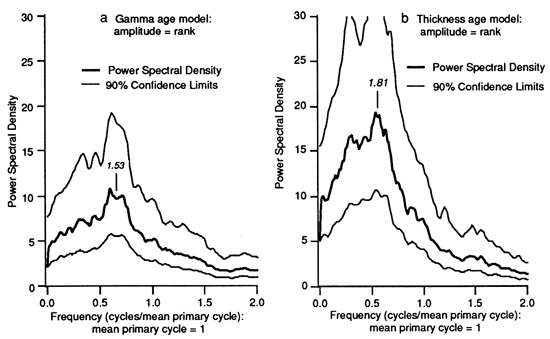
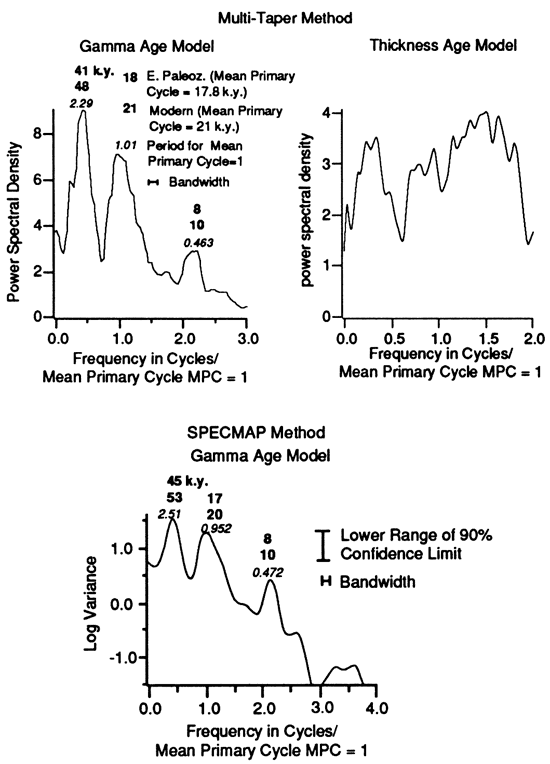
Based on the spectra from the gamma and thickness age models (figs. 8 and 9), the Trippe data have passed the next test. This test is for the presence of more than one spectral peak. We require that there be more than one spectral peak because, in the absence of a numerical time scale with sufficient resolution, the interpretation of the spectra in terms of orbital forcing models must be based on the ratios of at least two, and preferably more, spectral peaks. The spectra from the thickness and gamma age models clearly are not the same, indicating the degree to which the gamma corrections have altered the time series. For the gamma age model both the multitaper and SPECMAP techniques produced spectral peaks with essentially the same periods (although with somewhat different relative amplitudes), indicating that the presence of these peaks is independent of the spectral analysis method used.
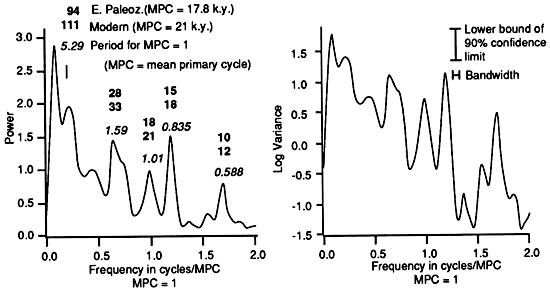
Figure 8--Results of multitaper spectral analysis (Thompson, 1982) for the Trippe cyclic section for (a) the gamma age model and (b) the thickness age model. The time series that were analyzed are shown in fig. 7. The data consist of 840 samples that are equally spaced at 1 k.y. The multitaper analysis used eight independent windows. The frequency is scaled so that the primary or measured cycles are unity. This gives a bandwidth (resolution on spectral peaks) of 0.1 cycles per mean primary cycle. The lightface numbers in italics are peak periods calculated directly from the frequency scale, referred to as the observed period in the text. Boldface numbers are the lightface periods multiplied by the mean value for the modern and estimated early Paleozoic precessional cycles from Berger (1977) and Berger et al. (1989). Note that the spectra for the gamma and thickness age models are different. In addition, the spectrum that uses the gamma age model appears to have eccentricity and precession index peaks. Although the resolution of the spectral peaks is low, the spectral separation of the eccentricity and mean precession index periods seems to be closer to that predicted for the early Paleozoic than for the modern (compare boldface periods for the gamma age model with those in fig. 12a). The prominent short-period peak at 10-12 k.y. is not unlike sub-Milankovitch periods that are observed in high-resolution modern deep-sea records, which are interpreted as combination tones of the two dominant precessional periods (Pestiaux et al., 1988; Ghil, 1987; Le Treut and Ghil, 1983) (see also fig. 14).
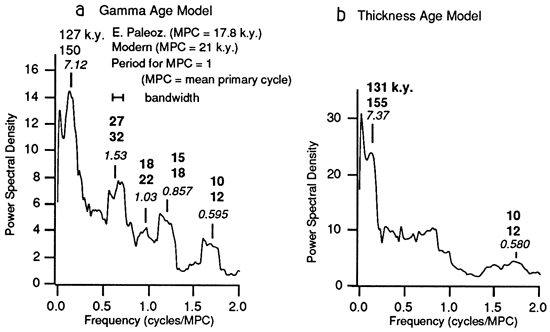
Figure 9--Results of the SPECMAP method (Blackman-Tukey; Hamming window) with statistics for Trippe cycle time series. Analysis was done only for the gamma age model with rank as amplitude. Time series was sampled at 559 evenly spaced intervals; number of lags = 186. The frequency scale and the periods indicated above the spectral peaks are obtained as described for fig. 8. Note the reasonably good similarity between the periods of the peaks detected by this method and the Thompson method (fig. 8).
Before interpreting the derived spectra from the Trippe cycles in terms of forcing mechanisms, we must determine whether the spectral peaks are significant. The Thompson method is capable of identifying line spectra as significant relative to the background spectrum by use of an F test. Given the uncertainties in the time scale and the nonlinearities inherent in the orbital-climate-sediment interaction, we would not expect sharp line spectra, even if the sediment cycles were due to orbital forcing. In fact, we observe broad peaks in the spectra of figs. 8 and 9. Although it would be valid to compare the observed spectrum with a forward-modeled spectrum of cyclic strata, this is difficult at present because of our poor understanding of the processes involved. A common method for assessing the significance of spectral peaks is to compare the spectrum to a white or red noise model scaled to the data variance. A white noise model is unlikely to be appropriate for these data (and it is in any case clear from the spectra in fig. 8 that such a model would find the low-frequency peak to be significant and the others not). Rather than assume a red noise model a priori, we use the observed statistics of the data to generate a null model.
Our null model simulates the observed cyclicity in the Trippe sample while randomizing the vertical succession of facies thicknesses. To do this, we construct a hypothetical cyclic sequence with three facies (A, B, and C) and the same number of cycles (40) as observed in the Trippe section. We further specify that the thicknesses of the facies in the hypothetical section have a Gaussian distribution and the same means and standard deviations as observed for facies A, B, and C in the measured section (table 1). We then construct a cycle by selecting a thickness from the Gaussian distribution for each facies using a Gaussian noise generator and stacking the facies in the correct order, from A at the base to C at the top. The process is repeated until the required number of cycles is reached. Cycles with only two facies are produced by assigning 0 thickness to all values from the Gaussian distributions that are equal to or less than 0. As can be seen in one example in fig. 7, the experiment produces an interlayering of three- and two-facies cycles similar to that in the measured section. We have generated 11 of these cyclic sequences and have constructed a gamma time series and a thickness time series for each. In most of the 11 trials the average cycle duration was close to the value from the Trippe data set, and we made the same adjustment as before, rescaling the time series to a length of 40.
We define the null model as the mean of the spectra from the 11 trials, obtained using the multitaper method (fig. 10). Only 11 spectra were generated in constructing the null model because calculation of the gamma spectrum is time-consuming, requiring human intervention to choose the optimum gamma values at each step. However, we ran the time-proportional-to-thickness null model to convergence (99 trials) and found that, apart from being smoother, it does not differ significantly from the 11-spectra null model shown in fig. 10a. This suggests that the gamma null model is also reasonably close to convergence (although the bump superimposed on the smooth curve at period 1.53 is probably an artifact). The null model for the gamma time series will be investigated in future work.
Figure 10--Spectra from the null model for (a) the gamma age model and (b) the thickness age model. The time series for the null model (shown in fig. 7) was sampled at 840 evenly spaced 1-k.y. intervals; the processing included pre-whitening and used 8 independent data windows. Ninety percent jackknife confidence limits are shown. The null model is based on a cyclic section with the same statistics as in the Trippe section and with the vertical succession of facies thicknesses randomized.
The null model is applied to the spectral data on the basis that, if the spectrum lacks significant spectral components, then we expect its spectrum to fall close to the spectrum of the null model. If the observed spectrum is significantly different from the null model in certain frequency bands, then we can take this as evidence of a nonrandom influence on the data at those frequencies. It is then valid to examine those frequencies for consistency with models such as the orbital forcing model.
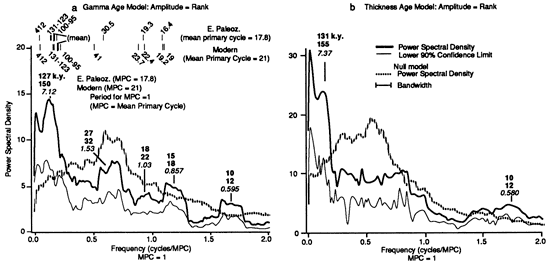
For the gamma age model from the Trippe sample, the lower 90% confidence bound of the spectrum touches or rises above the spectrum for the null model beneath the peaks at periods 7.12 and 0.595 (fig. 11). We can state that those peaks are significantly different from the null model at the 90% confidence level. The lower confidence bound rises abruptly beneath the peak at 0.857, reaching a level close enough to the null model spectrum to indicate that it is different from that model at only slightly less than 90% confidence. On the other hand, the prominent peak at 1.53 and the smaller peak at 1.03 cannot be distinguished from the null model. The statistics from the SPECMAP analysis seem to be consistent with these results (fig. 9). Thus there appear to be 3 distinct spectral peaks that are valid for comparing the Trippe spectra with a deterministic model, one at 7.12, one at 0.857, and one at 0.595 (fig. 11). We can state that at or close to the 90% confidence level these peaks are different from the spectrum for the null model and that they are not an artifact of circularity arising from the assumptions of essentially constant cycle period and constant y for each facies that were made in constructing the gamma age model. We also restate our point that the higher-frequency peaks have amplitudes too high to be explained away as overtones of lower-frequency peaks.
For the thickness age model from the Trippe sample, the lower 90% confidence bound rises above the spectrum for the null model beneath a peak at period 7.37 and beneath a much broader peak at period 0.580 (italicized numbers in fig. 11b). Thus we can say that these two peaks are different from the null model at the 90% confidence level.
Figure 11--Results with statistics of the multitaper spectral analyses of the Trippe cycle time series for (a) the gamma age model and (b) the thickness age model. The time series were sampled at 840 evenly spaced 1-k.y. intervals; the processing included pre-whitening and used 8 independent data windows. Ninety percent jackknife confidence limits are shown. Also shown is the spectrum for the null hypothesis from fig. 10. The frequency scale, the bandwidth, and the periods indicated above the spectral peaks are obtained as described for fig. 8. The predicted modern and early Paleozoic spectral line periods in the result for the gamma age model are from fig. 12a.
In the spectrum for the gamma age model (a), peaks that appear to correspond to eccentricity (7.12) and precession index (0.857) are significant at the 90% confidence limit when compared to the null model. This spectrum is produced by recalculating the spectral peaks assuming that the measured cycles are precessional. Also significant at the 90% confidence limit is the peak at 10 k.y., which may correspond to sub-Milankovitch peaks observed in some modern climatic records (e.g., fig. 14). Note that, as in fig. 8, the spectral distance between the inferred eccentricity and the precessional peaks is more like that predicted for the early Paleozoic than for the modern. Although the peak at 1.53 is close to the estimate for early Paleozoic obliquity, it cannot be distinguished from the single peak in the null model. As discussed in the text, tuning the time series with other assumptions for the duration of the average measured cycle results in a much poorer fit to the Milankovitch model (see also fig. 13).
In the spectrum for the thickness age model (b) with peaks recalculated by assuming precessional forcing of the cycles, one significant peak has a periodicity corresponding to a calculated Milankovitch peak; this is the eccentricity peak at period 7.37 (figs. 11b and 13). This peak is essentially the same as but less significant than the eccentricity peak in the gamma time series at period 7.12 (fig. 11a). In contrast to the result from the gamma-produced time series, the thickness time series lacks a distinct spectral peak at either of the expected periodicities of precession (compare with fig. 11 and see fig. 13). The other significant peak in the thickness time series, at period 0.580, is essentially the same as the high-frequency sub-Milankovitch peak at 0.595 in the gamma time series.
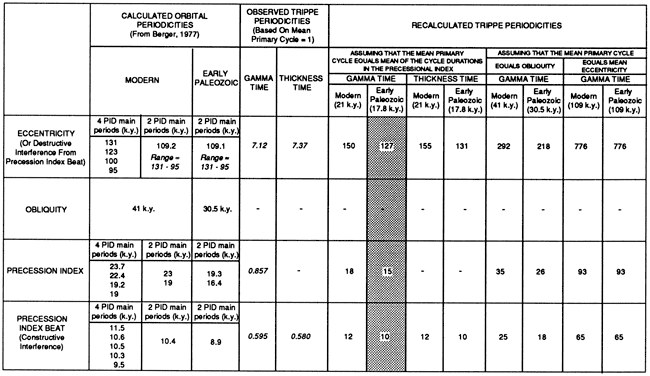
Recalculating the observed periodicities The observed periodicities (i.e., the periodicities in italics in figs. 8, 9, 11, and 14) of the spectra are calculated by assuming that the duration of the mean primary or measured cycle is 1. Consequently, to compare our spectra with the Milankovitch model, we must first recalculate the periods of the spectral peaks based on an appropriate value for the duration of the mean primary cycle. We cannot do this directly from the numerical time scales for the Cambrian because the numerical ages are poorly constrained.
We circumvented the problem of an inadequate numerical time scale by assuming values for the duration of the mean primary cycle that would be correct if the primary cycles were, in fact, orbitally forced, that is, forced by precession, obliquity, or eccentricity. We also take into account the changes that Berger et al. (1989) predicted in the frequencies of the orbital signal over geologic time. In this way we can calculate the periodicities of the significant peaks based on the values of the mean primary cycle and then compare them with the periodicities predicted by the Milankovitch model. If one of the choices for the duration of the mean primary cycle produces periodicities for all three significant peaks that are consistent with Milankovitch forcing, we would regard that as particularly strong evidence supporting the Milankovitch model.
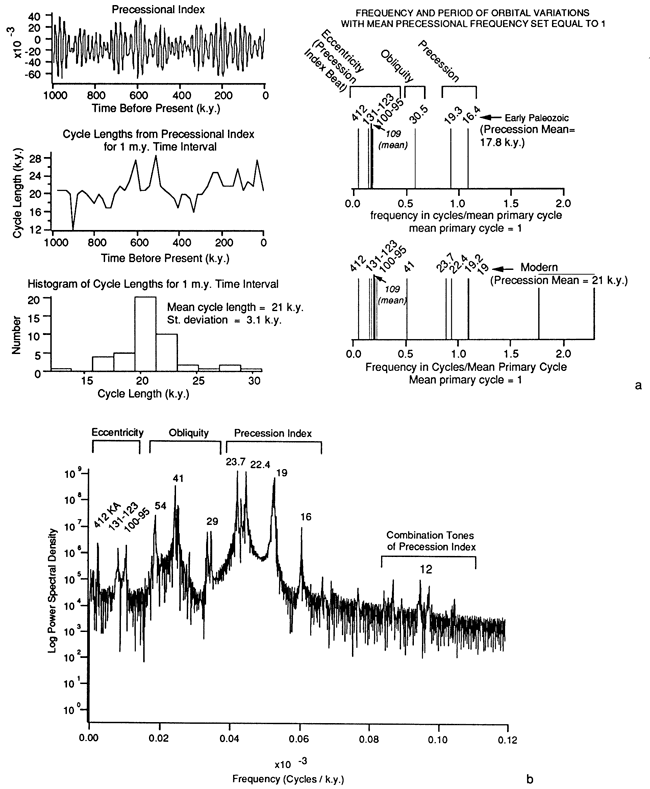
We begin by assuming that the cycles were forced by precession. For the modern astronomical system the cycle lengths for the precession index (precession modulated by the eccentricity; Berger, 1977) are variable, ranging from 12 k.y. to 32 k.y. over the past 1 m.y. (fig. 12a). They have a well-defined mean duration, however, of 21 k.y. with a standard deviation of 3.1 k.y. (fig. 12a). This is the mean of the two main periods of the precession index, 19 k.y. and 23 k.y. In the early Paleozoic (specifically at 440 Ma), however, line periods of the precession index are estimated to be 16.4 k.y. and 19.3 k.y., respectively (fig. 12a). We assume that the mean cycle length was the mean of these two periods, 17.8 k.y., although the exact value depends on phase and amplitude data, which are not known before approximately 5 m.y. ago. Thus, by analogy with the modern situation, we take the value of 17.8 k.y. as an approximation of the mean cycle duration for the Cambrian, recognizing that the result of Berger et al. (1989) is only a first estimate and that the calculation is for 440 Ma, whereas the Trippe cycles were deposited at about 530 Ma. The tuned periodicities of the spectral peaks, therefore, are given by multiplying by 17.8 k.y. the periods that were calculated for the mean primary cycle (= 1) (italicized periods in figs. 7-9). For comparison we also give the tuned periodicities for the modern mean value of 21 k.y. We emphasize that this tuning procedure does not force all the cycles to the same length. In fact, for a mean of 17.8 k.y. the durations of the Trippe cycles range from 12 k.y. to 38 k.y., a range that is similar to that observed in the modern precession index.
Figure 12--(a) Calculated astronomical data from Berger (1977) and Berger et al. (1988). The precession index is the angular precession of the perihelion modulated by eccentricity and is defined as Δe sin ω, where e is eccentricity and ω is the longitude of the perihelion relative to the moving vernal equinox (Berger, 1977). The computer-generated precession index was provided by Berger et al. (1988). The second plot at left shows the length of each cycle of the precession index, measured as time between negative-pointing peaks. (Other measures of cycle length show similar variations.) The third plot shows a histogram of these cycle lengths. Note the range of the cycle lengths in the precession index and the well-defined mean at 21 k.y. On the right, the occurrence of the dominant line periods of the orbital variations are shown for both the modern (assumed to be stable back to 5 Ma) and the early Paleozoic, as recently estimated by Berger et al. (1989). Frequency is scaled with the cycle means from the precession index equal to 1 for ease in comparing these predictions with our spectral results from the Cambrian cycles in other figures. The eccentricity signal in the 95-131-k.y. range consists of 4 spectral line periods (Berger, 1977), which are the combination tones of the 4 line periods of the precession index. These 4 eccentricity spectral lines form 2 groups that in both modern and early Paleozoic time are centered on 127 k.y. and 97 k.y. This is because eccentricity is essentially constant, at least on the scale of the Phanerozoic [see Berger et al. (1989)]. In modern climate records the eccentricity commonly appears as only one peak in the 95-131-k.y. range, either because the resolution at low frequency is not sufficient to distinguish the two peaks or because the direct eccentricity (at about 100 k.y.) has been amplified somehow.
(b) Spectrum of calculated July insolation at the top of the atmosphere at 65°N for the past 5 m.y. The spectrum is a raw fast Fourier transfonn with the time series sampled at 1-k.y. intervals. The spectrum shows the dominant periods in the short and long eccentricity cycles (destructive interference of the precession index line periods), the obliquity cycle, and the precession index (direct precession modulated by direct eccentricity) and the periods of constructive interference of the precession index line periods. Note that the strength of the eccentricity cycle is 5 orders of magnitude less than the strength of the precession index. Calculated insolation time series is from Berger et al. (1988).
Testing the spectra with other choices for the duration of the mean primary cycle is done in a similar manner. For the assumption that the mean primary cycle is equal to obliquity, the italicized periods can be multiplied by the early Paleozoic estimate of 30.5 k.y. (fig. 12a). Because eccentricity essentially does not change over geologic time, the test for eccentricity is given by multiplying the italicized periods by 109 k.y., which is the mean of the 4 dominant eccentricity line periods (fig. 12a).
If we recalculate the periodicities under the assumption that the primary cycles are precessional, we obtain a spectrum in which the periodicities of two of the three significant peaks correspond reasonably well to the predicted periodicities of the Milankovitch model (figs. 11a and 13). The most interesting result is that the correspondence appears to be better for the early Paleozoic estimates of the Milankovitch periodicities than for the modern ones. With a value of 17.8 k.y. for the mean primary cycle, the 0.857 peak has a period of about 15 k.y., which is close to 1 of the 2 periods of the estimated early Paleozoic precession index, 16 k.y. The low-frequency peak at 7.12 has a period of 127 k.y., placing it within the predicted range of eccentricity line periods (95-131 k.y.). The results of the SPECMAP analysis imply a similar degree of correspondence to the estimated early Paleozoic orbital signal (fig. 9). Tuning the gamma-produced spectra to the modern precession index produces a less compelling fit to the Milankovitch model. Assuming 21 k. y. for the duration of the mean primary cycle gives a period for the 0.857 peak of 19 k.y., which is the same as one of the periods of the modern precession index. The large low-frequency peak at 7.12, however, has a value of 150 k.y., which is larger than the calculated range of 95-131 k.y. for eccentricity line periods (fig. 13). Although these spectral data are encouraging evidence that we observe a shift in the frequencies of the orbital parameters close to that estimated by Berger et al. (1989), the evidence is weakened by the poor resolution of the low-frequency spectral peak (fig. 11a).
Figure 13--Summary of spectral data from the Trippe cycles compared with calculated modern and early Paleozoic orbital periodicities. Gamma time refers to the time series constructed using gamma values; thickness time refers to the time series constructed assuming that time is proportional to thickness; PID is the precession index. Periodicities from the Trippe section are for only those spectral peaks that are statistically significant at or close to the 90% confidence level relative to the null model as defined in the text. The eccentricity periods are equal to the precession index beat periods (destructive interference). According to Berger et al. (1988), these periods change little over Phanerozoic time (109.2 k.y. for the modern and 109.1 k.y. for the early Paleozoic). The range of 95-131 k.y. for the eccentricity periods also changes little over Phanerozoic time. Because only the two main precession index periods have been estimated for the early Paleozoic, only one constructive and one destructive precession beat period can be calculated. Note that only in the shaded column do the periodicities of all three significant peaks correspond to (or fall within the range of) calculated orbital periodicities. The difference between the modern and early Paleozoic eccentricity spectral peaks is poorly resolved, however, because of the large bandwidth (fig. 11a).
We should point out that the 5 line periods of the eccentricity cycle (412 k.y., 131 k.y., 127 k.y., 100 k.y., and 95 k.y.; fig. 12a) are combination tones of the 4 dominant line periods of the precession index, which is the precession modulated by the direct eccentricity. These combination tones appear in the spectrum of insolation arriving at the top of the atmosphere because celestial mechanics are nonlinear (e.g., fig. 12b) (Berger, 1977; Berger et al., 1988). The 4 line periods between 131 k.y. and 95 k.y. constitute the short cycles of the eccentricity, which have a mean period of 109 k.y., and the 412-k.y. period constitutes the long cycle of eccentricity. The variance in insolation received by the earth at both the long and the short eccentricity cycles is very small, amounting to, for example, 5 orders of magnitude less than that at the precessional cycle for July insolation at 65°N (fig. 12b) (Berger et al., 1988). The exceptional strength of the short eccentricity cycle observed in many climatic records requires some kind of nonlinear amplification [e.g., Ruddiman and Wright (1987)]. This can occur either through direct amplification of the eccentricity or by a beat between the main periods of the precession index. Therefore, to the extent that the amplitudes of the spectral peaks in the Trippe spectrum are approximations of the strength of the climatic response at the recalculated periodicities, the large amplitude of the low-frequency peak (7.12) is due to either amplification of the direct eccentricity in some way or a nonlinear response to the precession index. In fact, the facies boundaries and facies patterns in the Trippe cycles are suggestive of a nonlinear sedimentary response to sinusoidal orbital forcing; the change from one facies to the next is abrupt and the cyclic pattern is asymmetric (i.e., ABCABC. . .) rather than symmetric (i.e., ABCBABCB. . .). The mechanism responsible for the nonlinearity is an interesting question, especially because growth and decay of large ice volumes, one of the more viable mechanisms for nonlinearities in the Pleistocene climatic response to insolation changes [e.g. Ruddiman and Wright (1987)], is not likely to have been important in Cambrian time.
Given the consistency of 2 of the 3 significant peaks with the orbital model for the early Paleozoic, it is of interest whether the third significant peak, at 0.595, has any counterpart in that model. That this may be the case is suggested by comparing the Trippe spectrum generated by the SPECMAP method with a typical Pleistocene climatic record generated by the same technique (fig. 14). Although the Pleistocene record is from the deep sea, both examples are from equatorial latitudes. A prominent sub-Milankovitch spectral peak is, in fact, present at 12 ka in the modern record, and it is separated from the precessional peaks by approximately the same spectral distance as the 0.595 and 0.857 peaks in the Trippe spectra (fig. 14). Pestiaux et al. (1988) have suggested that sub-Milankovitch peaks, ranging from 12 k.y. to as short as 2 k.y., observed in deep-sea cores from the Indian Ocean are combination tones of the obliquity and precession index [see also Ghil (1987) and Le Treut and Ghil (1983)]. This interpretation would be consistent with our suggestion that the peaks in the eccentricity range are due to nonlinearities in the climate- sedimentary response to precessional forcing. Although we do not attempt to address the issue here, we recognize that an important question is, What might have caused a shallow marine carbonate system to respond nonlinearly to an insolation signal?
Figure 14--A late Pleistocene (last 750 k.y.) log variance spectrum from a well-known equatorial deep-sea record (Morley and Hays, 1981) compared with the Cambrian spectrum for the Trippe cycles using the gamma-corrected time series. Both spectra were produced using the same SPECMAP method (Blackman-Tukey with a Hamming window). The Pleistocene record was generated with a lag equivalent to one-third the number of data points sampled at even time intervals. The Trippe record is the same as that for the gamma age model in fig. 9. The spectrum was generated with 559 evenly spaced 1.5-k.y. samples; number of lags = 186. Only the lower bound of the 90% confidence interval is shown. Frequency scale for the Trippe spectrum assumes that the primary or measured cycle has the duration of the mean precessional cycle calculated for the early Paleozoic (17.8 k.y.). Note that a sub-Milankovitch peak is present at about the same spectral distance from the precessional peaks in both records. In the modern records this sub-Milankovitch peak has been interpreted as a combination tone of the two precession periods, 19 k.y. and 23 k.y. (Pestiaux et al., 1988; Ghil, 1987; Le Treut and Ghil, 1983). This comparison of modern and early Paleozoic spectra also contains evidence of the frequency shift in the precession index that Berger et al. (1989) estimated for the early Paleozoic (see also fig. 11a), but we emphasize that the resolution of the eccentricity peak in the early Paleozoic record is low.
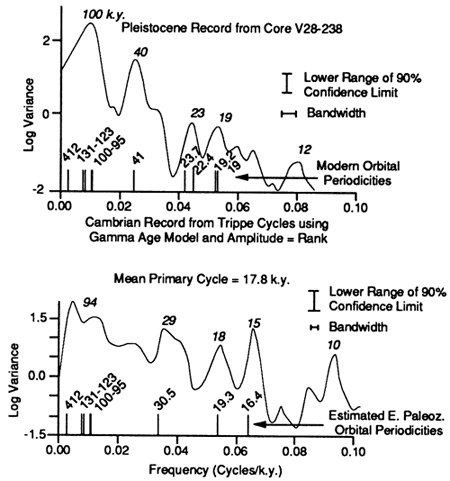
Although the weak spectral peak at 1.03 (italicized) cannot be confidently distinguished from the null model, it does fall near the other component of the early Paleozoic precession index, 19 k.y. (fig. 11a). It is not unusual, however, for only one of the two precessional terms to appear as a significant peak in modern climatic records [e.g. Ruddiman et al. (1989)].
The alternative possibility that the mean primary cycle corresponds to the early Paleozoic obliquity (30.5 k.y.) results in a value of 214 k.y. for the large low-frequency peak, 26 k.y. for the 0.857 peak, and 17 k.y. for the 0.595 peak (fig. 13). Only the 0.595 peak has a Milankovitch-like periodicity, corresponding to 1 component of the precession index. It is easily seen that multiplying the italicized numbers by the mean eccentricity line period of 109 k.y. produces a similar low degree of correspondence to the orbital model (fig. 13).
It may at first seem puzzling that we do not obtain a spectral peak at period 1, which is the value we assign to the mean cycle duration. A reason for the absence of this periodicity can be seen by comparing figs. 12a and 12b. The spectrum for the modern insolation signal received at the top of the atmosphere has five dominant periods in the precession index (fig. 12a). These are commonly observed as 2 periods in a typical spectrum from a climate record, one at 23 k.y. and the other at 19 k.y. However, the durations of the cycles in the time series of the precession index (left half of fig. 12a), have a strong mean of 21 k.y. The important point is that the mean of 21 k.y. for the duration of precessional cycles does not appear as a single period in the spectral analysis of the insolation or climate record. This is because the mean and range of the cycle durations are the result of the beating between the line periods of the precession index. Put another way, if the time scale is not too far off, spectral analysis will separate out the periods of the sine waves that are beating together in the precession index and produce at least two spectral peaks, one at 19 k.y. and the other at 23 k.y., flanking the value for the duration of the mean cycle (21 k.y.). (This will be true also for the long and short eccentricity cycles and for the combination tone in the 10-12-k.y. range.)
Thus, if time is scaled with reasonable accuracy with the gamma method and if the measured cycles were forced by the precession index, as we think is the case for the Trippe cycles, we should obtain a strong mean value for the duration of the primary cycle with a range of values falling off to either side in the time series. If we set that mean value to 1, we should not observe a single peak with a period of 1 in the spectrum. What should occur in the spectrum is at least 2 peaks on either side of and close to the period of 1. This is what we observe in the Trippe spectrum in fig. 11a.
If we recalculate the periodicities from the thickness time series assuming that the mean primary cycle is precessional, only one significant peak has a periodicity corresponding to a calculated Milankovitch peak; this is the eccentricity peak at period 7.37 (figs. 11b and 13). This peak is essentially the same as but less significant than the eccentricity peak in the gamma time series at period 7.12 (fig. 11a). In contrast to the spectrum from the gamma time series, the spectrum from the thickness time series lacks a distinct spectral peak at either of the expected periodicities of precession (compare figs. 11a and 11b and see fig. 13). The other significant peak in the thickness time series, at period 0.580, is essentially the same as the high-frequency sub-Milankovitch peak at 0.595 in the gamma time series.
Finally, it seems highly unlikely that the origin of the periodicities in the Trippe cycles is episodic movement along the inferred Middle Cambrian fault at the eastern edge of the House embayment (fig. 2). Although recurrence times of intraplate faulting may fall within the Milankovitch band (Cisne, 1986), faulting is not likely to have a multi-order periodicity, particularly one resembling an orbital signal. It would seem that the effect of intraplate faulting on cyclicity is more likely to be stochastic than deterministic, and if faulting occurred in central Utah during Middle Cambrian time, its effect is embedded in the stochastic noise of the Trippe spectrum.
The spectrum from the cyclic interval in the upper part of the Pierson Cove Formation is constrained by only 13 cycles, and the spectral data are less reliable than those from the Trippe section. Consequently, we have not attempted the same degree of statistical analysis that was applied to the Trippe data set. It is noteworthy, however, that the gamma age model noticeably improved the correspondence of the spectrum to the insolation model relative to that obtained from the thickness age model (fig. 15).
Figure 15--Results of the multitaper and SPECMAP methods applied to the Pierson Cove cycle time series in fig. 7. The multitaper method was done with 4 windows and 790 evenly spaced 1-k.y. samples of the time series; the SPECMAP method was produced using 646 evenly spaced samples of the time series, with number of lags = 199. No attempt was made to generate a null model for this spectrum because of the lower quality of the results relative to those from the Trippe cycles. The same peaks are present in the multitaper and SPECMAP spectra, strengthening somewhat their reliability. Based on the statistical procedures used in the SPECMAP procedure, the peaks probably are just barely significant at the 90% confidence interval. The poorer statistics relative to the Trippe data probably result, in part, from the short section of Pierson Cove cycles (see table 1).
Both the SPECMAP and the multitaper methods detected three broad peaks. All three peaks may be significant at or near the 90% confidence level, judging from the SPECMAP results (fig. 15). Two of these peaks, one at 1 and the other at 0.46-0.47, appear to have essentially the same periodicities as the presumed precession index and sub-Milankovitch peaks, respectively, in the Trippe spectra from the gamma age model (compare figs. 11 and 15). The occurrence of these two peaks in spectra from such different successions of cycles tends to increase their reliability. The third, at 2.29-2.51, does not seem to correspond to any Milankovitch periodicity or to any component in the Trippe record. The spectrum from the Pierson Cove Formation may be evidence that the primary or measured cycle was forced by precession, but this needs confirmation from additional field data, particularly a longer section (if one can be found), and more rigorous statistical analysis.
Recent forward models of shallow marine cycles, such as those in the Trippe and Pierson Cove sections, have led some to argue that the preservation potential of high-frequency (precessional) signals is relatively low. Although it is not our intent to address the problems of how the orbital-climate-sedimentary system might have worked in early Paleozoic time, the issue of preservation of high-frequency orbital signals must be faced because it bears on our interpretation of the Trippe and Pierson Cove spectral results.
In forward-modeling shallow marine peritidal cycles in terms of Milankovitch forcing, it is assumed that sea level rises and falls with a Milankovitch-like rhythm. This rhythm has been simulated by adding together 20-k.y., 40-k.y., and 100-k.y. sine waves, using the Pleistocene sea-level record with a substantially reduced amplitude as a guide [see, for example, Goldhammer et al. (1987, 1990) and Koerschner and Read (1989)]. The sea-level signal is superimposed on a shallow submarine surface that is subsiding linearly with time and with specified water depths and specified rates of sediment accumulation, progradation, and erosion. The problem arises from the fact that, according to the models, the falling part of the 100-k.y. cycle may expose the seafloor long enough to miss some 20-k.y. cycles entirely, producing condensed sequences. The rising part of the 100-k.y. cycle may prevent deposition of some of the shallow intertidal caps of the 20-k.y. cycles so that only the subtidal facies are formed, producing thick amalgamated cycles. The models imply that preservation of nearly all precessional cycles requires either high subsidence rates or a modification to the Pleistocene model so that the 100-k.y. sea-level component has a low amplitude relative to the 20-k.y. component (Goldhammer et al., 1990; Koerschner and Read, 1989).
An additional problem is that meter-scale cycles commonly are modulated by much larger-scale third-order cycles (hundreds of meters) that are probably formed by long-term (2-10 m.y.) changes in relative sea level. The Trippe Formation and the upper part of the Pierson Cove Formation, for example, may make up one such long-term cycle, with the upper part of the Pierson Cove Formation corresponding to the rising or accelerating segment and the Trippe Limestone corresponding to the falling or deaccelerating segment of the cycle (Bond et al., 1989). Recent forward modeling has implied that such third-order sea-level changes, if of sufficient amplitude, can cause missed precessional beats in much the same way as does the 100-k.y. component of the Milankovitch sea-level curve [e.g., Goldhammer et al. (1990)].
The forward models have been instrumental in studying the relation between rhythmic sea-level oscillations and cyclicity. However, so little is known about pre-Pleistocene climate and its control on sea level that it is difficult to predict which cyclic patterns are common and which are unlikely at any given time and place. During early Paleozoic time, for example, nearly all the continents were near the equator; there was little, if any, continental ice, and there were vast areas of epeiric seas, conditions substantially different from those during the Pleistocene. It is possible that for early Paleozoic time the Pleistocene sea-level model is fundamentally incorrect. In fact, it is likely that the sea-level model is not even valid for all of the Pleistocene. During late Pleistocene time, the largest changes in ice volumes and sea level corresponded to the 100-k.y. eccentricity period, a fact that is incorporated in most of the Milankovitch sea-level models. In middle Pleistocene time, however, the largest changes in ice volumes and presumably sea levels corresponded to the obliquity period (Ruddiman et al., 1989). An additional problem is that the subsidence rates are poorly constrained, especially for the early Paleozoic margins that Read et al. (this volume) have modeled; they may be much higher than has been assumed. Finally, with regard to the modulating effect of the long-term 2-10-m.y. third-order cycles, the amplitudes of these cycles are so poorly constrained that their effect on higher orders of cyclicity may be overestimated in the forward models. In addition, it should be kept in mind that some third-order cycles in subsiding basins may only be a consequence of changes in rates of a sea-level rise, and if so, the shoaling segments of the third-order cycles will not correspond to sea-level falls but rather to reductions in the rate of increase in accommodation.
Our spectral data imply that for relatively high accumulation rates, such as those we estimate for the Trippe and Pierson Cove strata, preservation of high-frequency signals may be much more common in peritidal cyclic records than the forward models have implied. The forward sea-level models need to be reevaluated in terms of data that are derived directly from the geologic record, and more emphasis should be given to mechanisms of nonlinear responses to the forcing signal.
We acknowledge the many helpful comments and criticisms in early stages of this work from Linda Hinov, Fred Read, Robert Goldhammer, Art Lerner-Lam, Jim Hayes, and Doug Martinson. We also thank Environment Canada Parks Service for permission to collect rock samples in Banff, Jasper, Yoho, and Kootenay national parks. Parts of the fieldwork for this project were supported by the National Science Foundation under grant EAR 88-17403 and by the American Chemical Society under grant ACSPRF 20852-ACB.
Algeo, T. J., and Wilkinson, B. H., 1988, Periodicity of mesoscale Phanerozoic sedimentary cycles and the role of Milankovitch orbital modulation: Journal of Geology, v. 96, p. 313-322
Anders, M. H., Krueger, S. W., and Sadler, P. M., 1987, A new look at sedimentation rates and the completeness of the stratigraphic record: Journal of Geology, v. 95, p. 1-14
Arthur, M. A., Dean, W. E., Bottjer, D., and Scholle, P. A., 1984, Rhythmic bedding in Mesozoic-Cenozoic pelagic carbonate sequences--the primary and diagenetic origin of Milankovitchlike cycles; in, Milankovitch and Climate, pt. 1, A. L. Berger, J. Imbrie, J. Hays, G. Kukla, and B. Saltzman, eds.: D. Reidel Publishing Company, Dordrecht, p. 191-222
Berger, A., 1977, Support for the astronomical theory of climatic change: Nature, v. 269, p. 44-45
Berger, A., 1988, Milankovitch theory and climate: Reviews of Geophysics, v. 25, p. 624-657
Berger, A., Loutre, M. F., and DeHant, V., 1989, Influence of the changing lunar orbit on the astronomical frequencies of pre-Quaternary insolation patterns: Paleoceanography, v. 4, p. 555-564
Berger, A., Loutre, M. F., and Laskar, J., 1988, New insolation values for the climate of the last 10 million years: Institut d'Astronomie et de Géophysique G. Lemaître, Scientific Report 1988/13, Université Catholique de Louvain, Louvain-la-Neuve, Belgium, 25 p.
Bond, G. C., Kominz, M. A., and Devlin, W. J., 1983, Thermal subsidence and eustasy in the lower Paleozoic miogeocline of western North America: Nature, v. 306, p. 775-779
Bond, G. C., Kominz, M. A., and Grotzinger, J. P., 1989, Role of thermal subsidence, flexure, and eustasy in the evolution of early Paleozoic passive margin carbonate platforms; in, Controls on Evolution of Carbonate Platform and Basin Development, P. Crevello, J. Wilson, R. Sarg, and F. Read, eds.: Society of Economic Paleontologists and Mineralogists, Special Publication 44, p. 39-61
Brady, M. J., and Koepnick, R. B., 1979, A Middle Cambrian platform -to-basin transition, House range, west of central Utah: Brigham Young University, Geological Studies, v. 26, p. 1-7
Cisne, J. L., 1986, Earthquakes recorded stratigraphically on carbonate platforms: Nature, v. 323, p. 320-322
Davis, J. C., 1973, Statistics and data analysis in geology: John Wiley & Sons, New York, 550 p.
Fischer, A. G., 1986, Climatic rhythms recorded in strata: Annual Review of Earth and Planetary Science, v. 14, p. 351-376
Ghil, M., 1987, Nonlinear phenomena in climate dynamics; in, Irreversible Phenomena and Dynamical Systems in Geosciences, C. Nicolis and G. Nicolis, eds.: D. Reldel Publishing Company, Dordrecht, p. 313-320
Goldhammer, R. K., Dunn, P. A., and Hardie, L. A., 1987, High frequency glacio-eustatic sea-level oscillations with Milankovitch characteristics recorded in Middle Triassic platform carbonates in northern Italy: American Journal of Science, v. 287, p. 853892
Goldhammer, R. K., Dunn, P. A., and Hardie, L. A., 1990, Depositional cycles, composite sea-level changes, cycle stacking patterns, and the hierarchy. of stratigraphic forcing--examples from Alpine Triassic platform carbonates: Geological Society of America, Bulletin, v. 102, p. 535-562
Grotzinger, J. P., 1986, Cyclicity and paleoenvironmental dynamics, Rocknest platform, northwest Canada: Geological Society of America, Bulletin, v. 97, p. 1,208-1,231
Halley, R. B., 1974, Repetitive carbonate bank development and subsequent terrigenous inundation, Cambrian Carrara Formation, southern Great Basin: Ph.D. dissertation, State University of New York, Stony Brook, 377 p.
Herbert, T. D., and Fischer, A. G., 1986, Milankovitch climatic origin of mid-Cretaceous black shale rhythms in central Italy: Nature, v. 321, p. 739-743
Herbert, T. D., Herba, C., Premoli Silva, I., Fischer, A. G., and Park, J., 1989, Improvements of Cretaceous geochronology using earth's orbital pacemaker--status and prospects (abs.): 28th International Geological Congress, v. 2, p. 51-52
Hintze, L. F., and Robison, R. A., 1975, Middle Cambrian stratigraphy of the House, Wah Wah, and adjacent ranges in western Utah: Geological Society of America, Bulletin, v. 86, p. 881-891
Imbrie, J., Hays, J., Martinson, D. G., McIntyre, A., Mix, A. C., Morley, J. J., Pisias, N. G., Prell, W. L., and Shackleton, N. J., 1984, The orbital theory of Pleistocene climate-support from a revised chronology of the marine 180 record; in, Milankovitch and Climate, A. Berger, J. Imbrie, J. Hays, G. Kukla, and B. Saltzman, eds.: D. Reidel, Dordrecht, p. 269-305
James, N. P., 1984, Shallowing-upward sequences in carbonates; in, Facies Models, 2d ed., R. G. Walker, ed.: Geological Association of Canada, 317 p.
Kepper, J. C., 1972, Paleoenvironmental pattern in middle to lower Upper Cambrian interval in eastern Great Basin: American Association of Petroleum Geologists, Bulletin, v. 56, p. 503-527
Kepper, J. C., 1976, Stratigraphic relationships and depositional facies in a portion of the Middle Cambrian of the Basin and Range province: Brigham Young University, Geology Studies, v.23,p.75-91
Kepper, J. C., 1981, Sedimentology of a Middle Cambrian outer shelf margin with evidence for syndepositional faulting, eastern California and western Nevada: Journal of Sedimentary Petrology, v. 51, p. 807-822
Koerschner, W.F., III, and Read, J. F., 1989, Field and modeling studies of Cambrian carbonate cycles, Virginia Appalachians: Journal of Sedimentary Petrology, v. 59, no. 5, p. 654-687
Kominz, M. A., and Bond, G. C., 1990, A new method of testing periodicity in cyclic sediments-application to the Newark supergroup: Earth and Planetary Science Letters, v. 98, p. 233-244
Lawson, C. L., and Hanson, D. J., 1974, Solving least squares problems: Prentice-Hall, Englewood Cliffs, New Jersey, 340 p.
Le Treut, H., and Ghil, M., 1983, Orbital forcing, climatic interactions, and glaciation cycles: Journal of Geophysical Research, v. 88, p. 5,167-5,190
Martinson, D. G., Pisias, N. G., Hays, J. D., Imbrie, J., Moore, T. C., and Shackleton, N. J., 1987, Age dating and the orbital theory of the ice ages--development of a high-resolution 0 to 300,000-year chronostratigraphy: Quaternary Research, v. 27, no. 1, p. 2-29
Matter, A., 1967, Tidal flat deposits in the Ordovician of western Maryland: Journal of Sedimentary Petrology, v. 37, p. 601-609
Menke, W., 1984, Geophysical data analysis--discrete inverse theory: Academic Press, New York, 260 p.
Morley, J. M., and Hays, J. D., 1981, Toward a high-resolution, global, deep-sea chronology for the last 750,000 years: Earth and Planetary Science Letters, v. 53, p. 279-295
Olsen, P. E., 1986, A 40-million-year lake record of early Mesozoic orbital climatic forcing: Science, v. 234, p. 842-848
Palmer, A. R., 1971, The Cambrian of the Great basin and adjacent areas, western United States; in, Cambrian of the New World, C. H. Holland, ed.: Wiley-Interscience, London, p. 1-78
Park, J., and Herbert, T. D., 1987, Hunting for paleoclimatic periodicities in a geologic time series with an uncertain time scale: Journal of Geophysical Research, v. 92, no. B13, p. 14,027-14,049
Pestiaux, P., van der Mersch, I., and Berger, A., 1988, Paleoclimatic variability at frequencies ranging from 1 cycle per 10,000 years to 1 cycle per 1,000 years--evidence for nonlinear behavior of the climate system: Climatic Change, v. 12, p. 9-37
Read, J. F., Grotzinger, J. P., Bova, J. A., and Koerschner, W. F., III, 1986, Models for generation of carbonate cycles: Geology, v. 14, p. 107-110
Rees, M. N., 1986, A fault-controlled trough through a carbonate platform--the Middle Cambrian House Range embayment: Geological Society of America, Bulletin, v. 97, p. 1,054-1,069
Ruddiman, W. F., and Wright, H. E., Jr., 1987, Introduction; in, The Geology of North America--North America and Adjacent Oceans during the Last Deglaciation, W. F. Ruddiman and H. F. Wright, Jr., eds.: Geological Society of America, v. K-3, p. 1-12
Ruddiman, W. F., Raymo, M. E., Martinson, D. G., Clement, B. M., and Backman, J., 1989, Pleistocene evolution--Northern Hemisphere ice sheets and North Atlantic Ocean: Paleoceanography, v. 4, p. 353-412
Shinn, E. A., 1983, Tidal flat environments; in, Carbonate Depositional Environments, P. A. Scholle, D. G. Bebout, and C. H. Moore, eds.: American Association of Petroleum Geologists, Memoir 33, p. 172-210
Thompson, D. J., 1982, Spectrum estimation and harmonic analysis: Proceedings of the Institute of Electrical and Electronics Engineers, v. 70, p. 1,055-1,096Weedon, G. P., 1989, The detection and illustration of regular sedimentary cycles using Walsh power spectra and filtering, with examples from the Lias of Switzerland: Journal of the Geological Society of London, v. 146, p. 133-144
Wheeler, R. F., 1980, Geology of the Sewing Machine Pass quadrangle, central Wah Wah range, Beaver County, Utah: Brigham Young University, Geology Studies, v. 27, pt. 2, p. 175-191
Kansas Geological Survey
Comments to webadmin@kgs.ku.edu
Web version April 21, 2010. Original publication date 1991.
URL=http://www.kgs.ku.edu/Publications/Bulletins/233/Bond2/index.html