Well Log Seismic Modeling
Previous seismic well log models generated from sonics in the Minneola
area suggested high-frequency seismic data could be used to differentiate
channels containing potentially productive sands from those with very thin
or no sands (Kruger, 1996). However, frequencies on the high end between
120 and 180 Hz were needed. Frequencies on the high end much lower than
this (60-90 Hz or less) would only result in identification of channel versus
no channel, and general channel thickness (thicker channels having a higher
amplitude reflection at, above, and below the top of the Morrow. This study
also suggested that overall channel thickness changes may interfere with
this signature, and anything less than a good signal-to noise ratio may
make the differences unrecognizable.
In order to determine if the previous seismic modeling results were reproducible
for other wells, and to further study the affects of varying channel thickness
and wavelet frequency content, additional models were run on eight wells
in the Minneola Complex which contained both sonic and density logs, and
which varied in both channel and productive sandstone thickness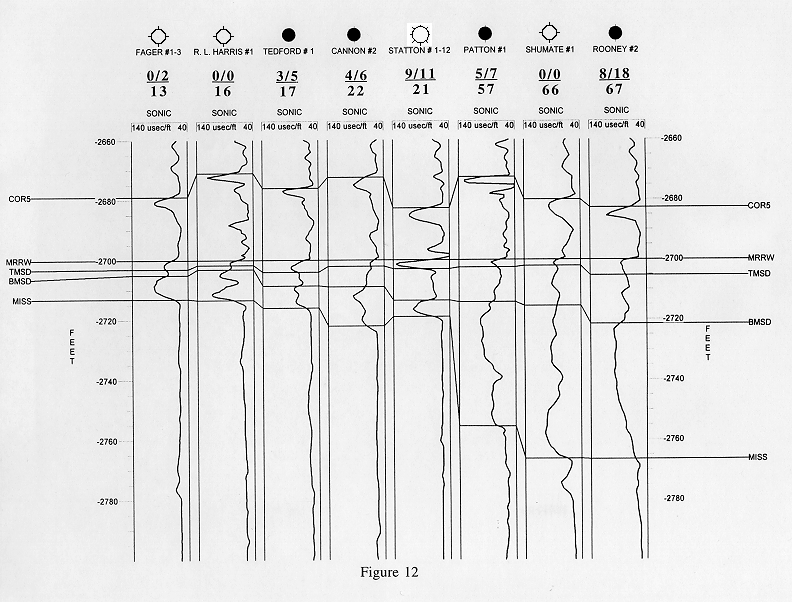 (Fig. 12). It would
have been best to use wells along the seismic lines acquired in this study.
Unfortunately, only two wells along the seismic lines contain sonic and
density logs. A test was run to determine if density logs alone could be
converted to pseudo-sonic logs for modeling purposes. However tests with
wells that contained both sonics and density logs showed that the models
constructed from converted density logs alone did not match very well those
developed with both sonic and density logs. In light of this test, no attempt
was made to construct seismic models along the seismic lines using just
density logs. The interpolated acoustic impedance model generated from the
eight wells with sonic and density logs in the Minneola Complex (Fig. 13) shows that there is a difference in impedance
near the top of the Morrow section between wells containing the thicker
sandstone and those containing no sandstone. However, it also shows that
there is a much larger lateral change in acoustic impedance as a channel
thickens up, because the lower impedance clastics of the Morrow section
are being compared to the higher impedance Mississippian limestones. This
larger change in impedance as the channel thickens could overwhelm the response
of the sandstone differences, particularly for lower frequency wavelets.
(Fig. 12). It would
have been best to use wells along the seismic lines acquired in this study.
Unfortunately, only two wells along the seismic lines contain sonic and
density logs. A test was run to determine if density logs alone could be
converted to pseudo-sonic logs for modeling purposes. However tests with
wells that contained both sonics and density logs showed that the models
constructed from converted density logs alone did not match very well those
developed with both sonic and density logs. In light of this test, no attempt
was made to construct seismic models along the seismic lines using just
density logs. The interpolated acoustic impedance model generated from the
eight wells with sonic and density logs in the Minneola Complex (Fig. 13) shows that there is a difference in impedance
near the top of the Morrow section between wells containing the thicker
sandstone and those containing no sandstone. However, it also shows that
there is a much larger lateral change in acoustic impedance as a channel
thickens up, because the lower impedance clastics of the Morrow section
are being compared to the higher impedance Mississippian limestones. This
larger change in impedance as the channel thickens could overwhelm the response
of the sandstone differences, particularly for lower frequency wavelets.
Results from the higher frequency model are shown in Figure 14. This model was developed by convolving the impedance
section with a zero phase Ormsby bandpass wavelet containing a low end slope
of 20-30 Hz, and a high end slope of 120-180 Hz. Although subtle, there
does appear to be a difference in seismic signature between wells containing
different sandstone thickness but similar channel thickness. For a thinner
channel (left half of model), this difference appears as an amplitude dimming
of both the trough near the top of the Morrow, as well as the peaks on either
side of it as sandstone thickness increases (Fig. 14).
For a thicker channel (right half of model), the signature is a little different.
As the channel thickens, the wavelet broadens up, turning into a wide trough,
trough doublet, or two troughs separated by a small peak. Comparison of
the two thickest Morrow to Mississippian sections in the Rooney and Shumate
wells show that the amplitude of the peak associated with the Mississippian
reflection decreases in amplitude as the upper sandstone thickness increases.
In addition, two troughs separated by a small peak near the bottom of the
Morrow section in the Shumate well (no sandstone) turns into a single, broad,
low amplitude trough in the Rooney well (1 8 ft. of sandstone). Another
change that occurs is a decrease in the isochron value between the Mississippian
peak and the COR4 peak going from the Shumate to the Rooney well (Fig 14). Comparison of the Shumate well with the Patton
well may be a little more difficult because of the thinner Morrow section,
however it does show a small peak developing just above the top of the Morrow
instead of near the base, possibly due to the presence of the sandstone
in the Patton well. In addition to the sandstone effects on the seismic
signature, thickening of the Morrow section due to channel incisement is
easily seen as an increase in the isochron value between the Mississippian
peak and the COR4 peak (Fig. 14).
Overall, the amplitude changes above seem to relate to both the velocity
change in the Morrow clastic section related to changes in sandstone content,
and overall thickness changes of the Morrow clastic section itself. The
amplitude changes being a result of tuning effects. With the higher frequency
model, the thinner Morrow clastic section on the left appears to be below
tuning thickness. However, the thicker sections towards the left appear
to be above tuning thickness because two troughs and a small amplitude central
peak appears (depending on the velocity). Therefore, tuning occurs at some
intermediate thickness and velocity such as between the Statton and Patton
wells (Fig. 14). This suggests that it may be
difficult, even with the higher frequency data, to separate the effects
of sandstone thickening and thinning from overall thinning and thickening
of the entire Morrow clastic section.
As will be discussed in later sections, the frequency content of the
seismic data acquired in this study did not approach that predicted in the
previous model. It was much lower. Based on synthetic seismogram ties with
the seismic data, it was determined that a new well log seismic model needed
to be developed using the frequency content of the seismic data near the
Morrow section. Results from this lower frequency model are shown in Figure
15. This model was developed by convolving the impedance section with a
zero phase Butterworth bandpass wavelet between 20 and 50 Hz with a 36 dB/octave
roll-off on the low end and a 72 dB/octave roll-off on the high end. As
can be seen, the wavelet in the lower frequency model is much broader, has
much lower resolution, and also has much less definition than the wavelet
in the higher frequency model. Although there are fairly pronounced changes
in amplitude of this wavelet, these changes are in large due to the thickening
of the overall Morrow clastic section and not to changes in sandstone thickness.
This model suggests that on the acquired seismic data, an increase in channel
thickness will be indicated by an increase in amplitude of the peaks above
and below the Morrow section, with a more substantial increase in amplitude
of the peak associated with the Mississippian reflection. In addition, the
intervening trough should increase in amplitude with increase channel thickness,
as well as a slight increase in the isochron between the two peaks (Fig.
15). Even though this model suggests that the
seismic data will be able to determine channel thickness, it is unfortunate
that it will not be able to identify the potentially produceable sandstones.
As with the higher frequency model, the amplitude changes associated
with the thickening and thinning Morrow clastic section indicates tuning
effects. In the case of the lower frequency model (Fig. 15),
the clastic section in all the modeled wells appears to be below tuning
thickness. Because of this, as the Morrow clastic section continues to thicken,
the amplitude of the reflection associated with it well become larger until
at some thickness greater than the maximum thickness in the model, the tuning
thickness will be reached and thickening beyond this will reduce the amplitude
of the reflection while lengthening the reflection and eventually splitting
it into two separate reflections.
e-mail : webadmin@kgs.ku.edu
Updated January 1999
The URL for this page is http://www.kgs.ku.edu/PRS/publication/OFR98_44/welllog.html
 (Fig. 12). It would
have been best to use wells along the seismic lines acquired in this study.
Unfortunately, only two wells along the seismic lines contain sonic and
density logs. A test was run to determine if density logs alone could be
converted to pseudo-sonic logs for modeling purposes. However tests with
wells that contained both sonics and density logs showed that the models
constructed from converted density logs alone did not match very well those
developed with both sonic and density logs. In light of this test, no attempt
was made to construct seismic models along the seismic lines using just
density logs. The interpolated acoustic impedance model generated from the
eight wells with sonic and density logs in the Minneola Complex (Fig. 13) shows that there is a difference in impedance
near the top of the Morrow section between wells containing the thicker
sandstone and those containing no sandstone. However, it also shows that
there is a much larger lateral change in acoustic impedance as a channel
thickens up, because the lower impedance clastics of the Morrow section
are being compared to the higher impedance Mississippian limestones. This
larger change in impedance as the channel thickens could overwhelm the response
of the sandstone differences, particularly for lower frequency wavelets.
(Fig. 12). It would
have been best to use wells along the seismic lines acquired in this study.
Unfortunately, only two wells along the seismic lines contain sonic and
density logs. A test was run to determine if density logs alone could be
converted to pseudo-sonic logs for modeling purposes. However tests with
wells that contained both sonics and density logs showed that the models
constructed from converted density logs alone did not match very well those
developed with both sonic and density logs. In light of this test, no attempt
was made to construct seismic models along the seismic lines using just
density logs. The interpolated acoustic impedance model generated from the
eight wells with sonic and density logs in the Minneola Complex (Fig. 13) shows that there is a difference in impedance
near the top of the Morrow section between wells containing the thicker
sandstone and those containing no sandstone. However, it also shows that
there is a much larger lateral change in acoustic impedance as a channel
thickens up, because the lower impedance clastics of the Morrow section
are being compared to the higher impedance Mississippian limestones. This
larger change in impedance as the channel thickens could overwhelm the response
of the sandstone differences, particularly for lower frequency wavelets.