
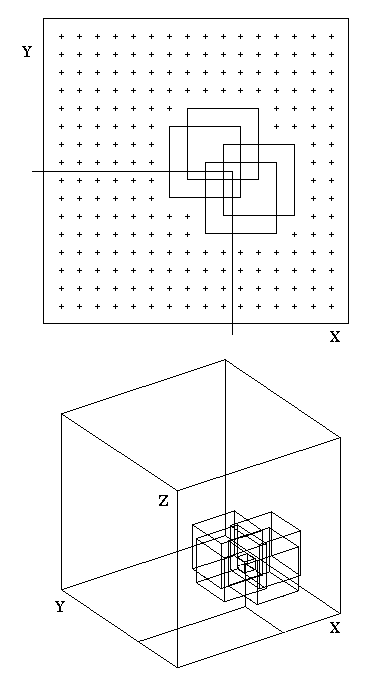
The key operational feature that gives Kipling its power is the way that it partitions multivariate space rather than the execution of complex algorithms or computations. The original inspiration for Kipling.xla was the CMAC (Cerebellar Model Arithmetic Computer), originally designed by Albus (1975) for robotic systems and still widely used today. The CMAC design subdivides variable space into a shingled framework of overlapping blocks whose incremental offsets describes a finer mesh of cells. The basic idea is shown for two- and three variable-space in the simplified diagrams to the right, but is easily extended to higher dimensions. Relatively complex patterns can be stored in this architecture, which results in large savings of computer memory as compared with a conventional gridded cell division. The contents of the blocks can be rapidly modified to collectively generate complex associations at much greater speeds than their equivalent computation through mathematical equations. This property is important for practical real-time performance in robot applications with control of elaborate articulated movements.
The implementation of the CMAC design by the robotics community predated the introduction of neural networks for artificial intelligence applications and has some design features in common. According to Burgin (1992), a CMAC is most closely comparable to a feed-forward neural network that is trained by back-propagation, but almost always outperforms the neural network. So, CMACs can be easily adapted to function as data analysis tools beyond their original purpose as robot controllers. While Kipling.xla does not implement the iterative operation of a CMAC device, it retains the data storage architecture design that is the core feature. In addition, the ability to store data either as frequencies of occurrence or properties of continuous or discrete variables allows Kipling to function both as a discrete classifier and a continuous predictor. Finally, Kipling was developed at the Kansas Geological Survey primarily for log analysis applications. However, the methodology is highly generalized, so that Kipling can be applied to almost any kind of data.
Further information on the use of CMAC in robotics can be found on the web site of the University of New Hampshire robotics group, including freely available C code implementing CMAC, with some additional options which help to overcome shortcomings of the traditional Albus CMAC implementation. Another interesting web site concerning the application of CMAC to robotics is provided by Russell Smith. Material available here includes Smith's 1998 Ph.D. thesis on his FOX robot control code, based on a modified CMAC algorithm, along with the C++ source code and some amusing MPEG movies of two simulated robots trained with the software -- a one-legged "hopper" and a bipedal walking robot.
Hagens and Doveton (1991) adapted the CMAC algorithm for use in representing a general function of multiple variables and applied the algorithm to mapping of a geological surface. The software developed for this work was a predecessor to the current Kipling software. Applications of Kipling to prediction of facies sequences are described in Bohling, Doveton, and Watney (1996) and Bohling, Doveton, and Hoth (1997).
The CMAC's discretization of variable space is quite similar to that employed in the averaged shifted histogram (ASH) proposed by Scott (1992). In fact, Scott's algorithm is somewhat more elaborate, in that the shifting of averaging bins along each axis is specified independently of that along other axes, rather than occuring in lockstep along all axes, as in the CMAC. The simpler CMAC discretization scheme results in a more efficient implementation, both in terms of execution speed and in terms of the amount of information that needs to be stored. On the other hand, the "learning" scheme employed by the ASH -- counting data points or averaging a response variable over each bin -- is much simpler than the iterative learning scheme employed in a CMAC. The algorithm implemented in Kipling can be considered a hybrid, combining the traditional Albus CMAC discretization scheme with the bin-wise averaging employed in the ASH.
Kipling Home || Next
Page--Continuous Example