KGS Cyclic Sedimentation Original published in D.F. Merriam, ed., 1964, Symposium on cyclic sedimentation: Kansas Geological Survey, Bulletin 169, pp. 631-636
Publications

Cycles and Psychology

by Edward J. Zeller

The University of Kansas, Lawrence, Kansas

Introduction

One of the companion papers in this volume (W.C. Pearn) has furnished an example of a new means for dealing with cyclic, or more properly, repetitive sedimentary sequences. With the development of high-speed computer techniques we have a tool at hand that will allow us to attain greater objectivity in dealing with complex stratigraphic successions. These methods are so new that some time will be needed to work them out for application to the routine problems of geology. Meanwhile, we must continue to use those established techniques to which we have become accustomed. In an evaluation of our present techniques we find that the stratigraphic sequences of the Pennsylvanian present us with problems which are not entirely geologic but are, in part, related to the psychologic make-up of the geologists themselves.

Psychologists, anthropologists, and philosophers of science have long recognized the fact that there is a fundamental need in man to explain the nature of his surroundings and to attempt to make order out of randomness (Nagel, 1961). The Western mind does not willingly accept the concept of a truly random universe even though there may be much evidence to support this view. The scientist unfortunately cannot escape from his own humanness, and in fact, it is this very need to explain and organize which furnishes him with the basic drive to become a scientist. Science, to an extent matched by no other human endeavor, places a premium upon the ability of the individual to make order out of what appears disordered. Therefore, the scientist more than anyone else needs to maintain his objectivity about his work, and perhaps even more rigorously, about himself.

Psychological Cycles

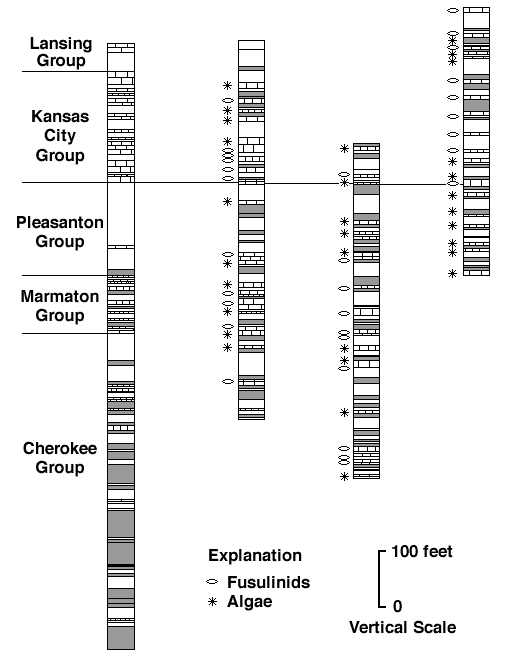
A test was devised to attempt to determine the extent to which psychological factors actually influenced geological thinking. Initially, a set of three logs plotted in the conventional form and each involving about 700 feet of section was given to a group of graduate students. They were asked to correlate the logs and, in every case, less than five minutes were required to complete the correlation. The correlation was frequently defended with considerable vigor when an attempt was made to question it or to suggest other possible correlations. The sections presented are reproduced in Figure 1 and show a typical Pennsylvanian type of cyclic sequence. The reader is asked to examine the sections carefully and to note the correlation line, which is that most commonly chosen by the students. A careful check of the correlation should be made with special attention being given to the cyclic nature of the beds, and the difficulty which this presents in making the correlation. It will be seen, however, that the correlation agreed upon by the students is the most appropriate one which can be made. The students were then given a log of a deep mine shaft located in Leavenworth County and asked to correlate the three logs with it. This section is also shown in Figure 1 with the stratigraphic units labeled. Again, the length of time necessary to complete the correlation was always less than five minutes, and there was little tendency to change the correlation of the first three logs because of new information given in the mine shaft section. As before, the reader is asked to examine the proposed correlation given by the students and see if he agrees with their identification.

Figure 1--Typical Pennsylvanian cyclic sequence: (1) lithologic log of deep mine shaft located in Leavenworth County with stratigraqphic nomenclature, and (2, 3, 4) logs of lithologies plotted in convention form (sequences numbered from left to right).

comparison of sample logs (on right) to log from mine in Leavenworth County

These tests showed correlation of cyclic sequences by inspection to be relatively easy. When confronted by sections which had a familiar appearance, no one had difficulty in making correlations and no more than a normal amount of hesitation was exhibited by any of the geologists to whom the test was given. At this point a psychological question arose. Suppose that geological data were presented in a different way. What would happen if we reduced a geologic section in the Pennsylvanian to a series of numbers which could be used to represent the various lithologies? It is obvious that computer techniques will require that such numerical representations be used. At the same time, such a presentation would provide the geologist with data in an unfamiliar form, and in this instance, we were seeking to determine the extent to which geologists had become dependent upon a conventionalized presentation of data.

There is considerable precedent for the use of numbers in representing lithologic units. Following the method proposed in Bulletin 22 of the Kansas Geological Survey (Moore, 1936) a series of columns was prepared. The numbering system is identical to that used in the description of the ideal cyclothem except that whole numbers are used instead of decimals. The stratigraphic section through the Kansas City Group was reduced to a column of numbers which is reproduced in Figure 2. When asked to correlate this section with three other columns also reproduced, the students encountered severe difficulty. The reader is asked to try his hand at a correlation using this set of columns. He will certainly find it much more difficult to make this type of correlation than was the case with the plotted logs. Part of the difficulty is related to the lack of thickness information. In a cyclic sequence, however, thickness should play a much less important role than that of the lithologic succession. Our tests have shown that geologists are indeed very dependent upon the mode of presentation of data, but the tests have shown something else far more important.

Figure 2--Stratigraphic sections through Kansas City Group represented by columns of numbers (numbers refer to those used in description of ideal cyclothem).

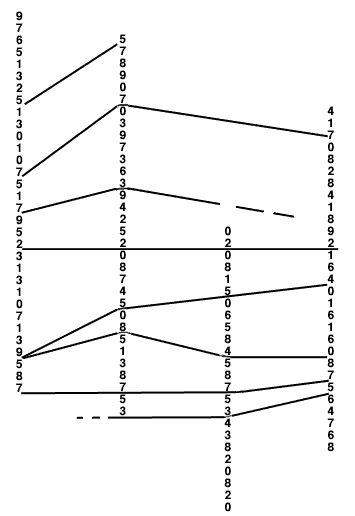
stratigraphic sections converted to numbers

In fact, both the students and the reader should have found it completely impossible to make any correlation either with plotted stratiraphic sections or with the columns of figures! In both cases only the left hand column was taken from real stratigraphic sections of actual rocks--the other sections were made up from columns of di,its taken from a random number table (Lawrence, Kansas, Telephone Directory, 1961) ! In the case of the plotted logs, the lithologies were assigned using the names for the units of the standard cyclothem and the thickness was determined by allowing an adj acent row of figures in the random number table to represent thickness in feet. Thus, except for the left hand column neither the logs nor the number sequences represent anything real, and they do not contain any genuine cyelicity.

If these stratiraphic sections and columns of figures are nothing more than a trick, a kind of joke, one can reasonably ask if thev have any value beyond that of entertainment. It should be apparent to all that psychological factors play a much larger role in these and other phases of geology than most geologists would care to admit. In these tests, cycles were seen repeatedly in purely random sequences, and correlations were made where none was possible. It can be argued that the writer did not act in good faith. It should be remembered, however, that "good faith" is a human value and is related to a set of human ethics which did not influence the natural processes that combined to produce the stratigraphic section with which we must work.

Let the reader be assured that it is not the writers' intention to show that cyclothems are "a false creation proceeding from the heat oppressed brain." The paper by W. C. Pearn shows by a method which is about as objective as possible that the ideal cyclothem as proposed by Moore (1936) is a very good approximation of the true natural sequence. No attempt is being made to imply that the Pennsylvanian of Kansas, as seen on the outcrop, is the result of totally random processes. The repetitive nature of the lithologies which appear in the outcrops cannot be ignored. Therocks that the geologist sees in the field are clearly less subject to false interpretation than a column of figures on a sheet of paper. Outcrops of rocks provide us with more than the three or four parameters of which we are aware with our conscious minds. More data are taken in by the senses of a geologist than appear in his field notes. Even though this is true, it is not unreasonable to ask that a closer look be taken at some of the kinds of stratigraphic successions which have been considered to be classic examples of true cyclicity.

The Two-component System

In order to hold complicating factors to a minimum we can begin by considering a situation in which only two types of lithologies are involved. This type of stratigraphic succession can often be found in certain portions of an evaporate basin in which alternating layers of salt and anhydrite were deposited. We see at once that we have a seemingly perfect cyclic sequence. The cycles consist of an anhydrite bed followed by a salt bed and the cycle is begun again with the deposition of the next anhydrite. The thickness of the beds is unimportant for we can always argue that thickness of beds is a function of rate and duration of deposition. It is clear that such a sequence is perfectly "cyclic" if we wish to extend the term to cover simple repetition. It is at once apparent, however, that the term becomes meaningless if we permit ourselves to apply it in such a broad manner.

Let us consider a sequence of numbers chosen by a roulette wheel. If we let red represent 1, and black represent 2, we might obtain a sequence something like this: 1 - 1 - 2 - 1 - 2 - 2 - 2 - 1 - 2 - 1 - 1 - 2 - 1 - 1. This random selection of numbers would result in a geologic section which would be an exact counterpart of the anbydrite-salt section. The geologist would be able to distinguish adjacent beds only if they were different but not if they were the same lithology. Two salt beds which were adjacent to each other would necessarily appear as only one lithologic unit. In this instance we see that random selection of components in a two-component system results in what would give the appearance of perfect cyclicity.

We must also remind ourselves that in nature, as in the roulette analogy, we are faced with the possibility that we will come up with a zero, which we can use to represent nondeposition, or a double zero, which can represent removal of beds. With a two-component system it is immediately apparent that we will not see the effect of zero or double zero unless we have sufficient lateral information to make it apparent. Neither nondeposition nor actual erosion will interrupt the seemingly perfect cyclicity of our two-component stratigraphic section. Objections can be raised to the use of the two-component system as an example of false cyclicity. One can contend that no geologist would be led astray to the extent that he would consider any two-component system as cyclic. Yet varves, a two-component phenomenon, furnish us with the only example of a stratigraphic sequence that is known to be truly cyclic in the strict mathematical sense. It should be remembered that a rigorous definition of the term cycle involves the parameter of time. Thus, in the strictest sense, each sedimentary cycle would have to be completed in the same amount of time. In the case of varve deposition this condition is met, and thus, they represent probably the only perfectly cyclic sedimentary sequences.

Returning to our original anhydrite-salt sequence, it can be argued that such a system is so rare that it almost never occurs in nature. One can usually expect a shale parting or a gypsum bed to break the sequence and thus dispel the illusion of cyclicity for the geologist who is studying the section. Following this line of reasoning it would appear that by increasing the complexity of the system we should have less difficulty in detecting incongruities in cyclicity. The incorporation of a third component should help greatly in allowing us to decide whether the system is random or cyclic.

The Three-component System

Another idealized system could be constructed using a three-component cycle. Such a cycle could begin with sandstone followed by an intermediate member of shale and completed with an upper member of limestone. This would represent the normal type of marine transgressive sedimentary sequence. We can proceed to set up a test to determine whether we can detect randomness in a hypothetical section which is plotted from randomly selected digits. In this instance 0 rep- resents either nondeposition or actual erosion, (1) sandstone, (2) shale, and (3) limestone. If we make up a section from fifteen digits taken from a random number table we obtain the section shown in Figure 3. In this instance we do not obtain fifteen separate lithologies because some of the adjacent numbers are the same and, in one case, a 0 occurs between two like digits. We now have a means to test the contention that a three-component system can be tested for cyclicity more easily and with more confidence than a two-component system.

Figure 3--Section made up from fifteen digits taken from a random number table to illustrate the threecomponent system.

stratigraphic section created from a three-component system

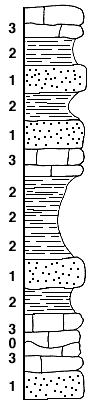
Would it be possible to conclude falsely from a randomly selected set of lithologic units that the sequence is cyclic? Let us assume that we have encountered this section in the field and see if it can be made to fit a cyclic pattern without resorting to some totally bizarre interpretation. Purely by chance, our section begins with sandstone. This is overlain by limestone and no intervening shale is present. Because we have no information other than that contained in our single section, we can easily conclude that the shale, which should belong between the sandstone and the limestone, was not deposited in this area but may be represented elsewhere. Next we find from our column of random numbers that we have encountered a period of nondeposition and another limestone is deposited upon the first. The fact that a period of nondeposition existed cannot be discerned from the section, however, and we are unable to distinguish the lower limestone from the upper one.

Above the limestone we have a shale followed by a sandstone. We can easily conclude that this represents a regressive phase rather than a transgressive phase of the cyclic deposition. Above the sandstone lies a thick shale unit which actually represents three individual digits and above that, a limestone. This, of course, comprises a perfect cyclic sedimentary sequence by our definition of the three-component system. Overlying the limestone is a sandstone. We conclude that this too is normal and that the regressive phases were either eroded or never deposited. The next transgressive phase is thus beginning. Further evidence for this conclusion comes from the fact that the next lithology is a shale, which is just as it should be. We find this shale overlain by a sandstone; however, we can easily take the view that the intervening limestone is missing because of erosion which occurred before the deposition of the sandstone. It could also be concluded that in this particular instance the extent of the transgression was not great enough to permit limestone deposition conditions to occur in this area. Finally, the top of the sequence shows a perfect repetition of the three lithologies which comprise our cycle.

From the preceding story, it will be seen that our stratigraphic section, composed of randomly selected lithologies, does indeed show most of the characteristics that can be expected in a truly cyclic sequence. At this point the reader may wish to complain that the writer has gone too far in making up samples with which to taunt his colleagues. Let the reader be assured, however, that the writer's humble efforts at creating confusion are of truly minute proportions when compared to those of nature.

We must seek to use every means at our command to avoid seeing in events or things a greater degree of order than that which actually exists. We should seek to eliminate, whenever possible, the confusion which arises between randomly occurring events and the nonrandom consequences of the events. Thus, the rising of a nearby land mass will effect the sedimentation in an adjacent basin in a highly predictable and by no means random fashion, but the elevation of the land may be a totally random event. Before we speak of cyclic sedimentation we should attempt to be sure that we are dealing with a sedimentary sequence which is the consequence of events which are, in fact, cyclic.

The stratigraphic record has been likened to the pages of a book in which we can read the history of the earth. Geologists are well aware that many pages are missing and that they are often obliged to read much between the lines. It is well to remember, however, that the meaning of every book is interpreted through the eyes of the reader, and these eyes are human. In all fairness we may ask if, in some cases, too much has not been read between the lines.

References

Lawrence, Kansas, Telephone Directory, 1961, Lawrence, Kansas, Southwestern Bell Telephone Co., columns 6 and 7, p. 48-49.

Moore, R.C., 1936, Stratigraphic classification of the Pennsylvanian rocks of Kansas: Kansas Geol. Survey Bull. 22, 256 p.

Nagel, E., 1961, The structure of science: Harcourt Brace & World Inc., New York, 618 p.

Selby, S.M., Weast, R.C., Shankland, R.S., and Hodgman, C.D., (eds.), 1962, Handbook of mathematical tables: Chemical Rubber Publishing Co., Cleveland, Ohio, p. 277-283.

Kansas Geological Survey
Comments to webadmin@kgs.ku.edu
Web version June 2002. Original publication date Dec. 1964.
URL=http://www.kgs.ku.edu/Publications/Bulletins/169/Zeller/index.html