Kansas Geological Survey, Current Research in Earth Sciences, Bulletin 258, part 1
Prev Page--Start || Next Page--Results and Discussion
![]()
![]()
![]()
Kansas Geological Survey, Current Research in Earth Sciences, Bulletin 258, part 1
Prev Page--Start ||
Next Page--Results and Discussion
![]()
With increasingly limited ground-water resources, reuse of treated municipal wastewater provides an alternative source of irrigation water for crops and landscaping. In addition, utilization of the nutrients in recycled wastewater as fertilizer may decrease the need for commercial fertilizers. However, municipal wastewater can contain high levels of nitrogen (N) and other constituents, such as salt, heavy metals, and pharmaceuticals (Pettygrove and Asano, 1985; Toze, 2006; Kinney et al., 2006), which can be detrimental to surface- and ground-water supplies if not carefully applied. Nitrate-N leaching into ground water is widespread in the U.S. Central Plains and elsewhere, and has been linked to the over-application of commercial fertilizers or animal waste (Bruce et al., 2003). The environmental impacts of treated wastewater-irrigation practices need to be evaluated to determine if and when these practices may affect ground water and what management practices can be changed to slow the downward migration of the particular nutrient of concern, nitrate-N, due to its potential to contaminate drinking-water sources. Understanding the environmental impacts of wastewater-irrigation activities can be addressed by careful field-data collection and analysis in combination with simulation models capable of assessing the consequences of certain factors and farming practices on N losses to the environment.
Bond (1998) pointed out the conflicting requirements of effluent irrigation, namely that leaching down the salts is essential to prevent salinization of the root zone, yet leaching will result in the movement of salt- and N-laden water to the deeper vadose zone and ground water. Research challenges in effluent irrigation include quantitative prediction of N transformations to evaluate scenarios for N management, and development of specific and more rigorous guidelines for wastewater applications (Bond, 1998).
Preferential flow occurring to some degree in most soils (Shipitalo and Edwards, 1996) is now generally recognized. In some soils, macropores can serve as important pathways for preferential flow that allows rapid gravitational flow of the free wastewater available at the soil surface or of the accumulated soil water above an impeding soil horizon, thus bypassing the soil matrix. Short-circuiting to ground water through macropores is of serious concern because of the possibilities of rapid transport of a portion of fertilizers, pesticides, and other chemicals applied on the soil surface. It is generally known that under flood or high-rate sprinkler irrigation, when water is allowed to pond on the soil surface, transport down preferential pathways becomes more likely and deep movement of solutes can be expected (Magesan et al., 1999). Flury et al. (1994) in a dye-tracing field study of 14 different sites found significant differences both in the flow patterns and depth of dye penetration for sprinkling versus flood irrigation, with the latter resulting in a dye penetration twice as deep as that for sprinkling, despite the fact that the intensity of the sprinkler system used was relatively high (96 mm/hr). As macropore development, preservation, and continuity can be strongly affected by soil management, such concerns have been exacerbated by the growing practice of minimum or no tillage. No-till allows chemical solutes in surface water applied on the soil to accumulate and enter macropores at the land surface; it also retains plant residues on the land surface thus enhancing worm activity and allowing worm holes and other macropore channels to stay open (Ahuja et al., 1993).
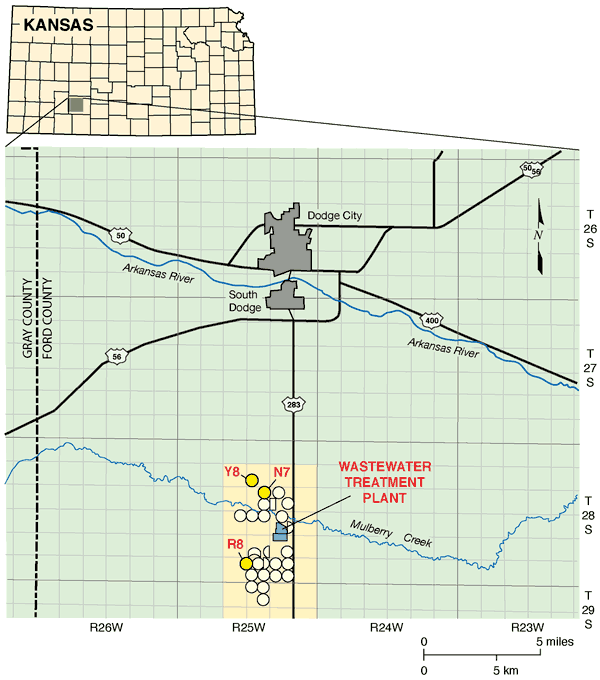
A long-term crop-irrigation project with treated wastewater south of Dodge City in semiarid to subhumid southwestern Kansas (fig. 1), which is underlain by the High Plains aquifer, is the focus of this study. Although the study area is characterized by a deep water table (ranging from 20 to 45 m below ground surface) and soils with a silty clay component (predominantly Harney and Ulysses silt loams, Dodge et al., 1965), evidence suggests nitrate-N is migrating to those water-table depths through the vadose zone (Zupancic and Vocasek, 2002). The use of the treated wastewater has resulted in relatively high soil nitrate-N concentrations (10-50 mg/kg) in the soil profile at the sites irrigated with this treated effluent, as well as in nitrate-N concentrations in ground water from a number of monitoring wells in the area exceeding the U.S. Environmental Protection Agency (USEPA) safe drinking-water limit of 10 mg/L (Zupancic and Vocasek, 2002). Zupancic and Vocasek (2002) estimated that once nitrate-N reached beyond the upper 1.5 m of the root zone, it could leach as much as 1.2 m in a wet year. Given that the average depth to the water table in the study area is more than 38 m (Sophocleous et al., 2006), preferential-flow processes may be involved in speeding up the transport of nitrate-N to the underlying water table. The U.S. Geological Survey's National Water-Quality Assessment and other studies in the central High Plains aquifer region suggest that N fertilizer and animal waste have reached the Ogallala portion of the High Plains aquifer due to increased recharge from irrigation and preferential-flow processes (Bruce et al., 2003).
Figure 1--Location of the study area (highlighted). Circular areas indicate irrigated fields; bright yellow circles are the study sites.
The Root Zone Water Quality Model (RZWQM, Ahuja et al., 2000) is a deterministic model that simulates the movement of water and nutrients over and through the root zone of a representative area in an agricultural field, and which also has the capability of addressing preferential-flow processes. In this study, we used a modified version of the RZWQM, named RZWQM2, that is capable of handling the deep-vadose-zone soil profiles.
Objectives of this study were
The Dodge City Wastewater Treatment Plant collects wastewater from Dodge City and a meat-packing plant. The collected wastewater is piped 17 km south of the city (fig. 1) into a wastewater-treatment facility, which consists of three covered anaerobic digesters and three aeration basins. The treated water is stored in lagoons with a capacity of more than 3,454 x 103 m3. A pumping system, consisting of several centrifugal pumps, distributes the water to irrigate more than 1,100 ha of cropland in 25 fields (fig. 1--circles). The system is managed by CH2M Hill Operations Management International (OMI) and monitored by the agronomic firm Servi-Tech, Inc., under contracts with Dodge City.
We established representative sites consisting of two main treated wastewater-irrigated monitoring sites (N7 and R8 in fig. 1) and one ground-water-irrigated site (control site; Y8 in fig. 1). Site R8 (37° 34' 32" N, 100° 3' 8" W) has treated-wastewater irrigation history (since 1986), whereas site N7 (37° 37' 9" N, 100° 2' 19" W) has a shorter-term treated-wastewater irrigation history since 1998. Crop-history records indicate that corn (Zea mays L.) was planted at site N7 each year since 1998, and at site R8 since 2003. From 1997 to 2002, site R8 was planted with alfalfa (Medicago sativa). In 2005, sites N7 and R8 were planted with corn on April 22-23, whereas site Y8 was planted with sorghum (milo). In 2006, all three sites were planted with corn. A LEPA-sprinkler irrigation system applied the treated wastewater at an average rate of 7.3 mm/day for Site N7, and 6.1 mm/day for Site R8.
On April 5, 2005, we collected three deep (15.2-m) soil cores from each of the sites for a number of physical and chemical analyses using a truck-mounted Giddings probe. Textural, soil hydraulic, and additional physical and chemical analyses were performed by NRCS personnel at the Lincoln, Nebraska, National Soils and Soil Mechanics Laboratories. (Due to sampling problems, the collected core for analyses of soil-hydraulic properties for site R8 was less than 5 m in length.) Nitrogen, carbon, and related analyses were conducted at Kansas State University (KSU) and Servi-Tech Soil Analysis Laboratories (see next section on soil and water chemical and isotopic analyses). The soil bulk density down to 15.2 m was determined from collected cores of known diameter by cutting the core in 15.2-cm increments, weighing them in the field, and then oven-drying them in the lab. The bulk density was also determined by the clod method (Grossman and Reinsch, 2002). Table 1 summarizes the measured soil physical properties by layer, which were subsequently used in the simulation model (explained further below).
Table 1--Measured soil physical properties for sites N7 and R8 by layer (in units employed in the RZWQM).
| Layer | Soil type | Horizon depth (cm) |
Bulk densitya (g/cm3) |
Porosityb (cm3/cm3) |
Sand fraction (g/g) |
Silt fraction (g/g) |
Clay fraction (g/g) |
Ksc (cm/hr) |
1/3-bar W.C.d,1 (0.03 MPa) |
15-bar W.C.d,2 (1.5MPa) |
Total organic carbone (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Site N7 | |||||||||||
| 1 | Silty loam | 0-23 | 1.280 | 0.517 | 0.056 | 0.686 | 0.258 | 1.3163 | 0.2260 | 0.1305 | 1.06 |
| 2 | Silty clay loam | 23-74 | 1.470 | 0.445 | 0.027 | 0.621 | 0.352 | 0.3911 | 0.2540 | 0.1690 | 0.53 |
| 3 | Silty clay loam | 74-168 | 1.300 | 0.509 | 0.033 | 0.624 | 0.343 | 0.7268 | 0.2710 | 0.1617 | 0.26 |
| 4 | Silty clay loam | 168-221 | 1.240 | 0.532 | 0.114 | 0.558 | 0.328 | 0.9829 | 0.2390 | 0.1410 | 0.24 |
| 5 | Silty clay loam | 221-363 | 1.380 | 0.479 | 0.115 | 0.554 | 0.331 | 0.2266 | 0.2070 | 0.1215 | 0.21 |
| 6 | Silty clay loam | 363-625 | 1.420 | 0.464 | 0.090 | 0.610 | 0.300 | 0.5431 | 0.2310 | 0.1185 | 0.05 |
| 7 | Silty loam | 625-848 | 1.350 | 0.491 | 0.126 | 0.631 | 0.243 | 0.7048 | 0.2340 | 0.1070 | 0.03 |
| 8 | Silty loam | 848-889 | 1.380 | 0.479 | 0.141 | 0.638 | 0.221 | 0.6966 | 0.2340 | 0.1260 | 0.02 |
| 9 | Silty loam | 889-945 | 1.410 | 0.468 | 0.267 | 0.513 | 0.220 | 0.6966 | 0.2480 | 0.0960 | 0.02 |
| 10 | Loam | 945-1079 | 1.520 | 0.426 | 0.344 | 0.416 | 0.240 | 0.1463 | 0.2335 | 0.1015 | 0.01 |
| Site N8 | |||||||||||
| 1 | Silty clay loam | 0-16 | 1.420 | 0.464 | 0.041 | 0.643 | 0.316 | 0.4480 | 0.3540 | 0.1500 | 1.66 |
| 2 | Silty clay loam | 16-29 | 1.490 | 0.438 | 0.036 | 0.659 | 0.305 | 0.4452 | 0.3530 | 0.1420 | 1.03 |
| 3 | Silty clay loam | 29-50 | 1.280 | 0.517 | 0.023 | 0.599 | 0.378 | 0.1553 | 0.3800 | 0.1780 | 0.75 |
| 4 | Silty clay | 50-68 | 1.210 | 0.543 | 0.017 | 0.553 | 0.430 | 0.0890 | 0.3950 | 0.2010 | 0.56 |
| 5 | Silty clay loam | 68-90 | 1.260 | 0.525 | 0.021 | 0.592 | 0.387 | 0.2799 | 0.3820 | 0.2170 | 0.42 |
| 6 | Silty clay loam | 90-140 | 1.520 | 0.426 | 0.030 | 0.627 | 0.343 | 0.8501 | 0.3660 | 0.1670 | 0.34 |
| 7 | Silty clay loam | 140-260 | 1.620 | 0.389 | 0.152 | 0.502 | 0.346 | 0.3237 | 0.2990 | 0.1310 | 0.17 |
| 8 | Silty clay loam | 260-300 | 1.610 | 0.392 | 0.194 | 0.483 | 0.323 | 0.1543 | 0.2800 | 0.1260 | 0.12 |
| 9 | Clay loam | 300-410 | 1.530 | 0.423 | 0.217 | 0.494 | 0.289 | 0.2968 | 0.2730 | 0.1190 | 0 |
| 10 | Silty clay loam | 410-484 | 1.540 | 0.419 | 0.188 | 0.496 | 0.316 | 0.1308 | 0.2920 | 0.1280 | 0 |
| acore method bcalculated assuming a particle density of 2.65 g/cm3 csaturated hydraulic conductivity performed on collected core samples according to ASTM-d5084 Flexible wall permeability tests d soil-water content (w.c.): 1--pressure-plate extraction; 2--pressure-membrane extraction e LECO combustion analyzer of acid-treated sample |
|||||||||||
A neutron probe (Campbell Pacific Nuclear {CPN} 503DR Hydroprobe) was used to collect moisture-data profiles to 15.2-m depth. The neutron probe was calibrated in the field based on core measurements collected from the access-tube borehole and on "wet" and "dry" corner plots, equipped with neutron-probe access tubes that were measured occasionally. Details of neutron access-tube installation and probe calibration are available in Sophocleous et al. (2006). Periodic (twice monthly for 2005, monthly for 2006) measurements of soil-water content at 0.15-m intervals within the upper 1.8 m and at 0.3-m intervals below 1.8 m down to 15.2 m were conducted throughout the growing seasons in 2005 and 2006.
Three suction lysimeters were installed in each site at various depths, shallow (1.6-1.8 m), intermediate (5.2-8.0 m), and deep (9.0-15.0 m), for collecting pore-water samples for occasional analyses. A Giddings auger was used to auger a 5.1-cm diameter hole and to install the suction lysimeters. Silica flour was used below, around, and slightly above the sampler ceramic cup to provide good contact with the soil. Approximately 30 cm of pellet-sized bentonite was then added with some water on top of the silica flour. Soil was backfilled on top of that bentonite layer to within 60 cm of the land surface. More bentonite was added to fill the hole to the surface to prevent surface-water from entering the hole. A 0.48-MPa vacuum pressure was put on each sample one week prior to sampling. The site R8 shallow, sites R8 and N7 intermediate-depth, and site Y8 deep lysimeters were the only ones to yield pore-water samples.
All the existing monitoring wells (14) in the area (shown in fig. 5) were sampled twice a year to check any nutrient-N impacts on the relatively deep water table, which ranges from about 21 m deep close to the usually dry Mulberry Creek to more than 45 m deep as one goes away from that creek (fig. 1). Additional water samples from monitoring, domestic, and irrigation wells and wastewater lagoons were periodically collected.
To explain deep occurrences of N concentrations through possible preferential pathways, we conducted two dye-tracer experiments in each of the two wastewater-irrigated study sites, site R8 in Harney soil (fine, superactive, mesic Pachic Argiustolls) and site N7 in Ulysses soil (fine-silty, mixed, superactive, mesic Aridic Haplustolls). Brilliant-blue food-coloring dye (FD&C Blue 1, tri-phenyl-methane dye) was used as a tracer because of its desirable properties of mobility and distinguishability in soils, and also because of its nontoxicity (Flury and Fluhler, 1994, 1995; Flury et al., 1994). Based on these studies, a dye concentration of 4 g/L was used to flood the test sites, which were enclosed in 91.4-cm by 152.4-cm wooden rectangular frames of 30.5-cm height, with approximately 750 L of dye solution per test site. It is expected that ponding would generate more preferential flow than sprinkling, as also was alluded to in the introduction. Additional details on these dye-tracer tests are presented in Sophocleous et al. (2006).
Total levels (inorganic and organic) of carbon (C) and N were determined on a dry weight-percent basis using a LECO CN 2000 combustion analyzer (LECO Corp., 1995). Calcium carbonate percentage was analyzed by pretreatment of a second LECO combustion sample with dilute (10% v/v) HCl. The total organic carbon is the % C in the acid-treated sample. The total inorganic carbon is then calculated as the difference in the treated and untreated values. Soil chloride is extracted from a 5-g sample with calcium nitrate and analyzed with the mercury thiocyanate colorimetric method.
Water analyses were conducted by the Kansas Geological Science (KGS) Analytical Services Section. The water samples were filtered through 0.45-µm membrane-filter paper before analysis. Specific conductance was measured to estimate chloride concentration and determine a dilution factor for the optimum concentration range of the analytical method. Nitrate, chloride, sulfate, and bromide concentrations were determined using a Dionex ICS Series 3000 ion chromatograph. Bicarbonate content was computed from an alkalinity determination using an automated titrimeter. Cation concentrations were measured using an inductively coupled argon plasma spectrometer. Charge-balance errors calculated for the well waters, for which measurements of all major and substantial minor constituents were completed, were all <2% and averaged 1.0%.
Natural-abundance nitrogen-15 isotope analysis is frequently used to assist in determining sources of N to ground water (Heaton, 1986). Nitrogen-15 (δ15N) values in the waters were determined at the Department of Environmental Sciences, University of Virginia. Samples of the dried nitrate containing salts dissolved in the waters were combusted at high temperature to N gas for analysis of their isotopic compositions. The δ15N was determined on a Micromass Optima isotope ratio mass spectrometer (IRMS) coupled with an elemental analyzer (EA), with an overall precision better than 0.5 ‰. The data are reported relative to a standard (atmospheric N2) defined to be 0 ‰, and expressed in δ notation as
δsample(‰) = (Rsample/Rstandard - 1) x 1000
where δsample represents δ15N, and R is the molar ratio of the heavier (15N) to the lighter (14N) isotope for the standard or sample (Hoefs, 2001). The analyses were run on nitrate in all samples except for the wastewater samples, which were run on total N (inorganic-N + organic-N).
The USDA-ARS developed a comprehensive agricultural systems model known as the Root Zone Water Quality Model (RZWQM) as a research tool to investigate the effects of agricultural management on crop production and environmental quality (Ahuja et al., 2000). The RZWQM is an integrated physical, biological, and chemical process model that simulates plant growth, and the movement and interactions of water, nutrients, and pesticides over and through the root zone for a representative area of an agricultural cropping system. It is a one-dimensional (vertical soil profile) model designed to simulate conditions on a unit-area basis. Details on all aspects of the model can be found in Ahuja et al. (2000).
The water-flow processes in the RZWQM are divided into two components: 1) infiltration into the soil matrix and macropores and macropore-matrix interaction during a rainfall or an irrigation event, modeled by using the Green and Ampt approach (Green and Ampt, 1911); and 2) redistribution of water in the soil matrix following infiltration, estimated by a mass-conservative numerical solution of the Richards' equation (Celia et al., 1990). Rainfall or irrigation water in excess of the soil-infiltration capacity (overland flow) is routed into macropores if present. The maximum macropore flow rate and lateral water movement into macropores in the surrounding soil are computed using Poiseuilles' law and the lateral Green-Ampt equation, respectively. Macropore flow in excess of its maximum flow rate or excess infiltration is routed to runoff. In the RZWQM, water can only enter the macropores at the surface. High-intensity rainfalls generally yield greater water flow and chemical transport in macropores than low-intensity rainfalls (Shipitalo and Edwards, 1996), and this is true with the RZWQM as well.
The hydraulic properties are defined by the soil-water characteristic or retention curves, and the unsaturated hydraulic-conductivity function. Those relationships are described by functional forms suggested by Brooks and Corey (1964) with slight modifications (Ahuja et al., 2000).
The volumetric soil-water content (θ) versus the capillary pressure head or matric suction head (ψ) relationship representing the water retention or characteristic curve is formulated as follows:
θ (ψ) = θs - A1 |ψ| for |ψ| ≤ |ψa| (1)
θ (ψ) = θr + B |ψ|-λ for |ψ| > |ψa| (2)
where θs and θr are the saturated and residual soil-water contents (cm3/cm3), respectively; ψ a is the air-entry or bubbling suction head (cm); λ is the pore-size distribution index (and represents the logarithmic slope of the water-retention curve); A1 and B are constants, where B = (θs - θr - A1 ψa) ψaλ and A1 was set to zero in our case, thus reducing equations (1) and (2) to the Brooks and Corey (1964) model. The Brooks-Corey parameters were obtained by fitting the RETC (RETention Curve) program (van Genuchten et al., 1991) to measured soil-moisture data.
The hydraulic conductivity (K) versus matric suction head (ψ) relationship representing the unsaturated hydraulic-conductivity function is formulated as follows:
K(ψ) = Ks |ψ|-N1 for |ψ| ≤ |ψa| (3)
K(ψ) = K2 |ψ|-N2 for |ψ| > |ψa| (4)
where Ks is the saturated hydraulic conductivity; N1, N2, and K2 are constants; and K2 = Ks|ψa|-N2; N2 = 2 + 3λ, and N1 was set to zero in our case, thus reducing equations (3) and (4) to the Brooks and Corey (1964) model.
The soil carbon/nitrogen dynamics module of the RZWQM model (Shaffer et al., 2000) contains two surface-residue pools (fast and slow decomposition), three soil-humus pools (slow, medium, and fast decomposition), and three soil-microbial pools (aerobic heterotrophs, autotrophs, and anaerobic heterotrophs). Despite the complexity of this organic-matter/N-cycling component, good estimates of initial soil-carbon content and nitrogen are generally the only site-specific parameters needed. The required inputs (e.g., fast pool, slow pool) are then usually determined through an initiation wizard and calibration (Ma et al., 1998).
The RZWQM included a generic crop model that can be parameterized to simulate specific crops (Hanson, 2000). However, the latest version of RZWQM2 (version 1.5) incorporated the Decision Support System for Agrometeorology Transfer, DSSAT4.0 suite of crop models (www.icasa.net/dssat/index.html; Ritchie et al., 1998), which can simulate detailed yield components and phenological development for specific crops. Of particular interest in our study is the corn model CERES-Maize, available as part of the DSSAT4.0. The CERES-Maize model has been extensively used worldwide for development of crop-management applications (Saseendran et al., 2005).
As mentioned previously, the RZWQM is designed to analyze soil and plant processes within the root zone, which in the recently released version 1.5, was extended down to 30-m depth. Because of model limitations (such as allowing only up to 10 model layers), we had to combine a number of soil horizons into a maximum of 10 layers as shown in table 1. A unit gradient was assumed for the lower boundary condition, set at 10.8 m for site N7 and 4.8 m for site R8 (the lowest depths for which we had detailed soil hydraulic analyses). The first neutron-probe soil-water profile measurements before crop planting in April 2005 were used as the initial soil-water depth distribution in the modeling.
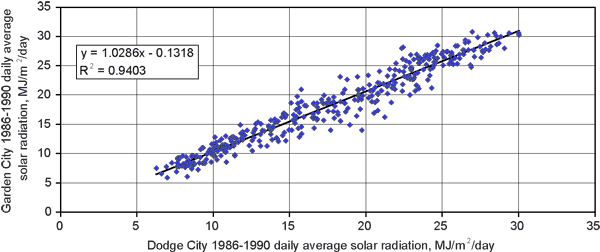
The model also requires detailed meteorological data, on a daily basis, and rainfall intensity data. Hourly precipitation and other meteorological data (except for solar radiation) were obtained from the Dodge City Municipal Airport weather station, 17 km northeast of the study sites; daily solar-radiation data were obtained from the Garden City Agricultural Experiment Station 80 km west-northwest of Dodge City, operated by Kansas State University. Due to similar geomorphic, land use/land cover, and climatic conditions between Garden City and Dodge City, no significant impacts on calculated water-budget components are expected from such climatic-data translocations. This is confirmed by comparing five years (1986-1990) of daily solar-radiation data when both Dodge City and Garden City weather stations were collecting such data (M. Knapp, Kansas State Climatologist, written communication, May 15, 2008). A linear regression of the daily average solar-radiation values at Dodge City and Garden City during the 1986-1990 period yielded an R2 of more than 0.94 (fig. 2). A year-by-year comparison indicated that the Dodge City total solar radiation as a percentage of that from Garden City was 97% for 1986, 99% for 1987, 93% for 1988, and 100% for both 1989 and 1990 (M. Knapp, State Climatologist, written communication, May 15, 2008). The model also requires specification of crop-management practices such as planting and harvesting dates and specification of irrigation and fertilization events, as well as the chemical quality of irrigation.
Figure 2--Comparison of daily average solar radiation from 1986 to 1990 for Garden City and Dodge City, Kansas.
For accurate simulations, RZWQM must be calibrated for soil hydraulic properties, nutrient properties, and plant-growth parameters for the site and crops being simulated (Hanson et. al., 1999), as there are significant interactions among the different model components. Available data for 2005 were employed in calibrating the model, whereas the available data for 2006 were reserved for verifying ("validating") the model. Calibration targets included the biweekly (during 2005) and monthly (during 2006) neutron soil-water measurements, soil nitrate-N analyses, and harvested-corn grain yields. The number of parameters and processes in the RZWQM are so numerous that it is exceedingly difficult to decide which ones to optimize and what optimization scheme might be appropriate, if at all feasible. As a result, such agricultural-system models as the RZWQM are usually parameterized by trial-and-error or iterative processes (Ahuja and Ma, 2002). In this paper, we followed the detailed procedures for calibrating the RZWQM as laid out by Hanson et al. (1999) and Ahuja and Ma (2002). In addition, a series of sensitivity analyses were conducted to identify the most important parameters in both the soil and plant portions of the model affecting model output and thus to use in model calibration (Sophocleous et al., 2007).
The model-calibration strategy we used was as follows: the RZWQM was first calibrated for soil hydraulic properties, which included the pore-size distribution index, λ, and the saturated soil-water content, θs, for each modeled soil layer. (Sensitivity analysis indicated that these parameters were among the most sensitive in our case.) The model was then equilibrated with respect to the initial C/N pool sizes for the fast and slow decomposition-residue pools; slow, medium, and fast decomposition-humus pools; and the three microbial pools (aerobic heterotrophs, autotrophs, and anaerobic heterotrophs) (Hanson et al., 1999). No laboratory procedures are known to effectively determine the sizes of these pools (Ahuja and Ma, 2002). Therefore, because previous management at a site determines the initial state of a soil in terms of its organic matter and microbial populations, simulations with previous management practices will usually create a better initial condition for those parameters (Ma et al., 1998). After entering all the model inputs and parameters, we began by estimating the three humus organic-matter pool sizes (based on the measured organic-carbon depth profiles shown in table 1) at 5, 10, and 85%, for fast, medium, and slow pools, respectively, and set the microbial pools at 50,000, 500, and 5,000 organisms per gram of soil, respectively, for aerobic heterotrophs, autrotrophs, and facultative heterotrophs, as recommended by Ahuja and Ma (2002). RZWQM was initialized for the organic-matter pools by running the model for 12 years prior to the 2005-06 actual simulation periods. A 12-year initialization run was suggested by Ma et al. (1998) to obtain steady-state conditions for the faster soil organic pools.
Following initialization and equilibration of the carbon and nitrogen (C/N) pool, the crop parameters were calibrated by trial-and-error adjustments to match observed crop phenology and yield as simulated by the CERES-Maize dedicated corn model, available as part of the DSSAT4.0 suite of crop models incorporated in the latest model version RZWQM2. Nutrient (nitrogen) and plant (corn) components are interrelated because adjustment of crop parameters affects both nitrate-leaching loss and crop yield. Corn calibration parameters included four phenological and two growth parameters as follows: i) thermal time from seedling emergence to the end of the juvenile phase (P1, expressed in degree days above a base temperature of 8°C, °Cd); ii) photoperiodism coefficient (P2, expressed as days delay in tassel initiation per hour increase in photoperiod, d/hr); iii) thermal time from silking to physiological maturity (P5, °Cd); iv) thermal time between successive leaf-tip appearances, known as phyllochron interval (PHINT, °Cd); v) maximum possible number of kernels per plant (G2); and vi) kernel-filling rate (G3, mg/d). We based adjustments of these parameters for corn within the range of values used for Kansas environments (Pachta, 2007; Dogan et al., 2006; Roman-Paoli et al., 2000; Kiniry et al., 1997).
Because the N-related and plant-growth parameters are difficult to measure with independent experiments, an accurate description of the soil-water-related processes as far as possible is required to minimize N-simulation errors. Therefore, particular effort was expended in calibrating the soil-water hydrologic processes first before proceeding with the plant and N-related parameter calibration.
Three statistics were used to evaluate the simulation results: i) root mean squared error (RMSE) between simulated and observed values, eq. (5); ii) relative root mean square error (RRMSE), i.e., RMSE relative to the mean of the observed values, eq. (6); and iii) mean relative error (MRE) or bias, eq. (7).
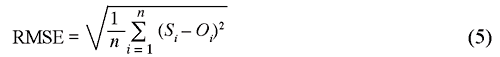

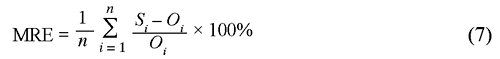
where Si is the ith simulated value, Oi is the ith observed value, Oavg is the average of observed values, and n is the number of data pairs.
The RMSE reflects the magnitude of the absolute mean difference between simulated and experimental results, whereas the RRMSE standardizes the RMSE and expresses it as a percentage that represents the standard variation of the estimator (Abrahamson et al., 2005). The MRE indicates if there is a systematic bias in the simulation. A positive value indicates an overprediction and a negative value an underprediction.
Several management scenarios were simulated using reduced fertilization treatments of 50% and 40% of the actually applied wastewater-N totals at site N7 during 2005 and 2006. Also, reduced irrigation totals of 88, 75, and 50% of actually applied amounts in 2005 were evaluated while maintaining the same irrigation scheduling. In all the above-mentioned management scenarios, the resulting Nitrogen-Use Efficiency (NUE, see further below) and grain yields were evaluated.
Nitrogen-Use Efficiency (NUE) is a term used to indicate the relative balance between the amount of fertilizer N taken up and used by the crop versus the amount of fertilizer N "lost," and can be defined as follows (Hu et al., 2006):
![]()
To compute NUE, the RZWQM2 model was re-run with a zero-N treatment, and the results were used in eq. (8).
Prev Page--Start || Next Page--Results and Discussion
Kansas Geological Survey
Placed online Feb. 12, 2010
http://www.kgs.ku.edu/Current/2010/Sophocleous/02_intro.html
email:webadmin@kgs.ku.edu