Morlet Wavelet

⁽¹⁾ "The detection of cyclicity in sedimentary strata can be important to the understanding of the factors controlling sediment depositions. The presence of cyclic patterns and changes in their character have important consequences for geological interpretation, changes in wavelength may indicate changes in depositional facies."

Morlet Wavelet Energy Coefficient W(a,b)

W(a,b) =

1 −− √a

+∞ ∫ -∞

f(t)Ψ((t-b)/a)dt

where Ψ(t) = exp(-t2/2) exp(2πjfot); 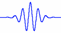is the Morlet Wavelet, a plane wave modified by a Gaussian envelope and f(t) is the Digital LAS File Log Curve with the following variables defined as,

	fo	is the fundamental frequency of the wavelet
	a	is a dilation/compression scale factor that determines the charactersitic frequency in units of feet.
	b	represents the translation in units of feet.

W(a,b) provides space-scale analysis rather than space-frequency analysis, proper scale-to-frequency transformation allows analysis that is very close to space-frequency analysis. Reducing the scaling parameter "a" reduces the support of the wavelet in space, which covers higher frequencies, and vice versa. Therfore 1/a is a measure of frequency. The parameter "b" indicates the location of the wavelet window along the space axis. This changing (b,a) enables computation of the wavelet coefficients W(a,b) on the entire space-frequency plane.

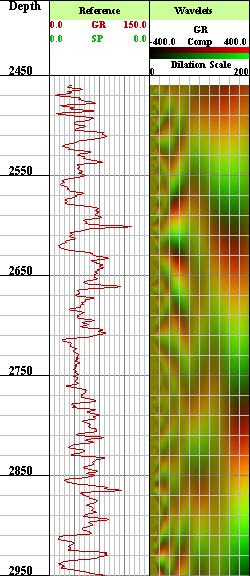
Example Output:
Real Part of W(a,b) as Red Imaginary Part of W(a,b) as Green	Magnitude of W(a,b)	Phase arctan[W(a,b)]

References:
(1) Detection of Cyclic Patterns Using Wavelets: An example Study in the Ormskirk Sandstone, Irish Sea By Nestor A. Rivera, S.Ray, Jerry L. Jensen, Andrew K. Chan, and Walter B. Ayers Mathematical Geology, Vol. 36, No. 5, July 2004

Author: John R. Victorine jvictor@kgs.ku.edu