
Kansas Geological Survey, Educational Series 6, originally published in 1988
Previous Page--Introduction, Geologic Time ||
Next Page--Fossils
Rocks are one of the main sources of information for geologists. By comparing rocks and minerals and their locations, geologists can estimate approximately how old the rocks and minerals are. They can tell if a rock was formed on dry land, on an ocean floor, or deep inside the earth.
Other people besides geologists have found rocks and minerals useful. The Indians used native stone to make tools, weapons, and pottery. Early settlers constructed buildings, bridges, and fences out of limestone and sandstone. Indians and settlers used natural caves for protection and rock outcrops for lookouts; and they carved pictures, called petroglyphs, in the rock walls.
Figure 8. Ancient carvings on rock exposures are called petroglyphs. This one was carved in sandstone by Indians in Ellsworth County in central Kansas.

Kansas also has had its share of fortune hunters. More than once people have traveled through the state seeking valuable minerals such as gold and silver.
In 1541 the Spanish explorer Francisco Vazquez de Coronado was told of an Indian land named Quivira where gold and other riches were abundant. His desire to find Quivira led him into a territory that is now part of Kansas. But Coronado and his men went away disappointed. They never located gold, which apparently existed only in Indian legends.
More than 300 years later in the 1880's, hundreds of prospectors flocked to Logan County in western Kansas hoping to find silver. Thousands of dollars were spent to stake claims, but only traces of nickel ore were found. Scientists who visited the area didn't think conditions were right for either silver or nickel to form. The traces of the minerals were probably found in rocks from outer space, called meteorites, which had collided with Earth.
Although not much gold or silver has been found in Kansas, coal, gypsum, lead, zinc, chalk, salt, volcanic ash, limestone, sandstone, clay, sand, oil, and gas have all been found and used to make various products. Because of their many uses, rocks, minerals, and other natural resources add to the wealth of Kansas. They bring money and jobs. They also add to the environmental wealth. Undisturbed rocks and minerals add color, form, and beauty to the landscape.
Figure 9. Oil and gas were first discovered in Kansas in the 1860's. Wells, such as this oil well in Comanche County in southwest Kansas, are now located throughout the state.

We know that rocks and minerals are all around us, but what are they?
Minerals occur naturally in the Earth. They are not made by people. They also are inorganic. This means they are not made from living material; no part of a mineral was ever alive.
All minerals are made of smaller units called elements. A few minerals, such as gold and silver, are made of only one element. These minerals are called native elements. Sulfur is the only native element found in Kansas. All other minerals are a combination of two or more elements.
Minerals can be identified by their color and hardness. The scale for hardness ranges from 1 to 10; the harder a mineral is, the higher its number. A diamond, which is very hard, rates a 10. Garnet is one of the hardest rocks found in Kansas. It is a 7 and is so hard it can scratch window glass.
Pyrolusite, another Kansas mineral, is at the lower end of the hardness scale. It is a 1 or 2 on the scale and is soft enough to leave a black streak when rubbed on a piece of paper.
Galena, sphalerite, pyrite (fool's gold), halite (salt), calcite, anhydrite, gypsum, mica, and quartz also are found in Kansas. Many other minerals occur in the state, but none in large quantities.
Figure 10. Geodes are formed when ground water deposits minerals in rock cavities. They measure from 1 to 12 inches (2-27 centimeters) in diameter.

Figure 11. Kansas has many minerals, but most are found only in small quantities. Minerals vary in color and hardness. The hardness of each mineral is rated on a scale from 1 to 10, with 1 being the softest and 10 being the hardest; most minerals fall somewhere in the middle.

A rock is usually made of one or more minerals. Most rocks we see on the Earth's surface have been broken up into small pieces. Sand, gravel, clay, and silt are all made of particles worn from rocks.
Rocks that are buried are called subsurface rocks because they are located below the Earth's surface. Subsurface rocks are often found in large slabs called beds. Beds are sometimes seen at the surface, but often in Kansas they are covered by soil. They can be several feet thick, extend for many miles, and be layered one on top of another. Unless the beds are disturbed by forces such as earthquakes or volcanoes, the deeper beds are usually older than the ones closer to the surface.
Figure 12. Layers of sedimentary rocks often form in flat beds. Sediment deposited on the Earth's surface compresses earlier deposits into hard rock. When beds are formed in this way, the deepest ones are the oldest.
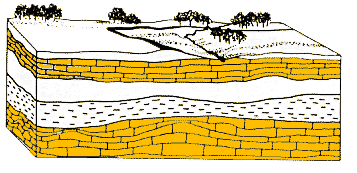
Figure 13. Sometimes wind and water carve hills and valleys into the surface that are later buried. Magma also may force its way up from deep inside the Earth. When magma cools, a solid rock is formed within the layers of rock already there. This type of formation is called an intrusion (A). Rocks inside the earth may break and shift along a fault (B). These shifts, if big enough, may cause earthquakes.
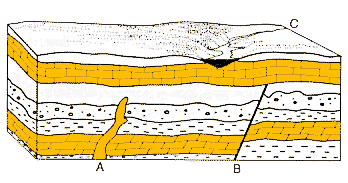
Sometimes rocks that were once underground are exposed by erosion. These exposures are called outcrops. In some places, the hills have been cut away to make roads more level. Areas cut away for roads are called roadcuts.
Figure 14. Underground rock beds, formed over millions of years, were exposed when part of a hill was cut away for a road.

Rocks are organized into three categories depending on the way they are formed. These categories are sedimentary, igneous, and metamorphic.
Sedimentary rocks, the most common rock at the surface in Kansas, can be found throughout the state. They may be formed from other rocks that were worn down by erosion into small pieces, such as sand and gravel, called sediment. A solid rock may be formed if the sediment is covered by great thicknesses of other sediment and rocks and pressed together, or if it is cemented together by minerals.
Organic material, which is anything that was once alive, may also be pressed together into a solid mass. Fossils of shells and tiny microscopic plants and animals, left behind when ancient seas dried up, are found in much of the Kansas chalk and limestone. Other common sedimentary rocks in Kansas are clay, shale, bentonite, silt, siltstone, sand, sandstone, dolomite, salt, and coal.
Clay is composed of very fine particles eroded from rocks and minerals. These particles are so finely worn that they can only be seen with a microscope. Clays may be a variety of colors-white, gray, black, red, yellow, tan, or green-and are often mixed with larger particles of other sediment such as sand and pebbles. Bricks, dishes, and other ceramic products are made from clay, which is molded and then hardened by heat.
Figure 15. Bricks made of clay pave this sidewalk in Lawrence.

When clay and silt are compacted into a solid rock, it is called shale. Shale erodes easily into clay when exposed in outcrops and roadcuts. Like clay, shale can be many different colors and is common in Kansas and throughout the world. It is used to make bricks and as an ingredient in cement.
Bentonite is a type of clay formed from altered volcanic ash. Most types of bentonite swell when they absorb water. Deposits of bentonite have been found in several locations in western Kansas.
Silt consists of particles larger than clay particles but smaller than sand particles. It is deposited by wind and water. Loess (pronounced lus) is a windblown silt found in many areas of Kansas. Thick loess deposits occur in northeast Kansas where rocks and gravel were ground down by glaciers and water. Later the dried mud was picked up by the wind. Much of it settled near the margins of the glaciers. But loess also covers much of the surface in western Kansas where it was spread around by ferocious dust storms.
When silt is compacted and cemented together, it forms a rock called siltstone, which is found in eastern Kansas.
Sand particles vary in size and can easily be seen without a microscope. Sand often contains eroded particles of rocks and minerals carried downstream by rivers and creeks. Two minerals, quartz and feldspar, are commonly found in sand.
Sand deposits are widespread in the state, especially along streams and river valleys and in old river deposits. Sand hills also cover large areas of south-central and southwest Kansas.
Figure 16. Wind and water have shaped this sand dune near the Arkansas River in Kearny County in southwest Kansas.

When sand is cemented together, it is called sandstone. Sandstones in Kansas range in color from a light tan to brown to reddish-orange to bright orange. The different colors are caused by a variety of minerals and impurities. Sandstone deposits are found throughout Kansas, and buildings made of sandstone blocks can be found in areas where it is most abundant.
Limestones are common in Kansas. They are usually found where seas once covered the land. They also can be formed from deposits in freshwater or on dry land, but nonmarine limestones are less common.
Most of them were formed from accumulations of marine plants and animals after they died and sank to the sea floor. If conditions were right, millions of tons of plant and animal debris were deposited and eventually compacted together. When the sea dried up, large slabs of rock were formed, often stretching for hundreds of miles in every direction. Some plant and animal remains, such as shark's teeth and dinosaur bones, have been preserved as fossils in limestone.
Figure 17. The Lebold-Vahsholtz house in Abilene was completed in 1880, ands was built of limestone brought from more than 100 miles away in Russell and Ellis counties.

Sea or freshwater shells, plants, or animals such as algae, corals, clams, oysters, brachiopods, bryozoans, fusulinids, and crinoids are sources of calcite, which is the main mineral found in limestone. Thick deposits of these plants and animals form limestone.
Figure 18. A limestone bridge crosses Diamond Creek in Chase County.

Limestones containing only one mineral--calcite--are white. But most limestones contain other minerals, for example iron oxide (rust), and organic remains. These cause limestone to vary in color, especially when the rocks are exposed to weathering elements such as air and water. Limestones in outcrops and roadcuts are usually off-white, tan, or yellow, and may be streaked with other colors.
Figure 19. This character, carved in limestone, guards the front door of the Marion County courthouse in Marion.

Some buildings are made of limestone. Crushed limestone also is used to surface roads and is an ingredient in cement. Limestones are found at the surface in many parts of eastern Kansas but are not as common in central and western Kansas. However, chalk, which is a type of limestone, is found in some central and western areas.
Chalk is a type of limestone often formed from the shells of small, single-celled animals called foraminifera. Pure chalk is fairly soft and white, but it usually has impurities that cause it to be different colors. Many fossils have been found in the chalk beds of western Kansas, among the most extensive chalk beds in the world.
Figure 20. Pieces spall off a wall of chalk in Gove County.

Dolomite is similar to limestone; however, it is composed chiefly of a mineral also named dolomite, rather than calcite. Calcite and dolomite are often found together. The rock they form may be called dolomitic limestone or dolomite, depending on the quantities of calcite and dolomite it contains. Dolomite, which is found in some areas of southern and central Kansas, has many of the same uses as limestone.
When plants die in a swamp, their decaying remains are buried in mud. As they become buried deeper in the Earth, the decaying plants are pressed together and heated, forming a firm, brittle rock called coal. Coal can be burned to produce heat or to generate electricity. Before they had electricity, people often heated their homes and other buildings by burning coal. Early steam engines were fired by coal, but today trains run on diesel oil.
Figure 21. Coal is most likely to form from deposits in swampy areas with heavy vegetation. Coal takes millions of years to form.

Figure 22. Coal was used to fuel this train as it traveled through Kansas around the turn of the century (photo courtesy of the Kansas Historical Society).

Rocks that have been changed from one kind of rock to another by heat and pressure are called metamorphic, which is Latin for "changed form." Limestone changes to marble; shale to slate, schist, and gneiss; and sandstone to quartzite. Marble, slate, and quartzite are much harder rocks than limestone, shale, and sandstone. Metamorphic rocks are rare in Kansas. Quartzite, which is found in a small area in Woodson County, is the only native metamorphic rock found at the surface.
Quartzite boulders can be found throughout northeastern Kansas, but they were not formed there. Glaciers carried the rocks in from South Dakota, Iowa, and Minnesota. They are red, brownish red, or purple.
Igneous rocks are formed when a hot liquid, called magma, cools and changes from a liquid state to a solid state. They may form slowly underground or rapidly at the Earth's surface. When magma reaches the surface, it is called lava. Lava flows out of a volcano and quickly hardens after an eruption. Although most lava reaches the surface through volcanoes, it may also flow out of deep cracks in the earth without building a mountain.
Kansas doesn't have an active volcano, but lava did flow onto the surface as recently as 90 million years ago when dinosaurs still roamed the Earth. Hot magma forced its way up from over 100 miles below the Earth's surface in two small areas of eastern Kansas. The hot liquid, which spread upward through cracks in other underground rocks, cooled and hardened, forming a rock called lamproite in Woodson and Wilson counties and one called kimberlite in Riley County.
In one area of Riley County, lava flowed onto the surface but a volcanic cone was never formed. The kimberlite formed from the lava is now buried. Lamproite and kimberlite found at the surface in Kansas were exposed when the rock above was eroded away. Diamonds have been found in kimberlites and lamproites in other parts of the world, but none has been found yet in Kansas.
Granite, another type of igneous rock, has been found mixed with lamproite in Woodson County. It is older than the surrounding surface rocks and was formed deep in the Earth. Lamproite magma carried it toward the surface, where it is now exposed.
Some igneous and metamorphic rocks have traveled into Kansas from other places. Volcanic ash, basalt, granite, and quartzite have been carried in by wind, glaciers, and water.
One type of rock found in Kansas was not formed anywhere on Earth. Meteorites have the most unusual origin of any sediment carried--or, in this case, dropped--into Kansas. Meteors are rocks in outer space that usually vaporize before reaching the Earth's surface. As they enter the atmosphere and begin to disintegrate, meteors are seen as streaks of light called shooting or falling stars. The few meteors that do reach the Earth's surface are called meteorites.
Identifying meteorites in Kansas is easier than in other places, because they don't look like other Kansas rocks. Meteorites usually have a burned appearance, are pitted, and are denser than other rocks. Iron meteorites, consisting of heavy metals, iron, and nickel, are the easiest to identify. Stony meteorites are harder to identify because they look like volcanic rocks. Because Kansas has few volcanic rocks and lots of wide-open spaces, many meteorites have been found in the state.
Previous Page--Introduction, Geologic Time || Next Page--Fossils
Kansas Geological Survey
Placed on web Feb 11, 2016; originally published 1988, reprinted 1995.
Comments to webadmin@kgs.ku.edu
The URL for this page is http://www.kgs.ku.edu/Publications/Bulletins/ED4/02_rocks.html