Kansas Geological Survey, Ground-water Series 8, originally published in 1985

Originally published in 1985 as Kansas Geological Survey Ground-water Series 8. This is, in general, the original text as published. The information has not been updated.
The containment of pollutants in freshwater aquifers supplying ground water for agricultural, municipal, and industrial use is an important management task. In recent years, the extent and magnitude of surface-introduced pollutants in ground-water reservoirs have been documented, and efforts are being made to identify management options that satisfy the demands for freshwater while containing the pollutant in the aquifer at a reasonable cost.
This report summarizes the design and construction of a management model that seeks to minimize the cost of pumping fresh ground water while restricting movement of the polluted ground water to within a specific area. The management model was applied to a hypothetical but realistic aquifer, and the results were analyzed. The demonstrative model discussed in this particular study will be further extended to identify management options in a contaminated portion of the Equus Beds aquifer in south-central Kansas.
A demonstrative ground-water hydraulic management model is used to identify the optimal strategy for allocating limited freshwater supplies in a hypothetical aquifer affected by brine contamination from surface waste-disposal ponds. The cost of pumping from a network of potential supply and interception wells is minimized over a 5-yr planning period, subject to a set of hydraulic, institutional, and legal constraints. Hydraulic constraints are formulated using linear systems theory to describe drawdown and velocity variables as linear combinations of supply- and interception-well discharge decision variables. Successful application of the optimal management strategy suggests that the model formulation can feasibly be applied to define management options for the contaminated Equus Beds aquifer in south-central Kansas.
Despite increased regulation of surface waste-disposal operations that have been identified as potential sources of ground-water contamination, increasing evidence shows that the quality of existing ground-water supplies is being threatened by the consequences of past disposal practices. For the case of surface waste-disposal operations that have been terminated as a result of perceived contamination potential, movement of remaining pollutants into the subsurface and through ground-water supplies may pose a transient but serious hazard to current freshwater resources in affected aquifers. The problem of managing groundwater reserves under such circumstances must therefore focus on alleviating the residual effects of past disposal practices on limited freshwater resources.
Ground-water hydraulic management models have been developed over the past several years in response to the growing need to systematically relate the hydraulic behavior of the flow system to the cost of utilizing scarce aquifer supplies during identification of optimal management policy (Gorelick, 1983). Using linear systems theory, the physical principles of ground-water flow or solute-transport as described by a simulation algorithm can be coupled with an optimization model that minimizes the costs or maximizes the benefits of utilizing scarce ground-water resources, subject to various legal, institutional, and hydraulic constraints (fig. 1). Linear systems theory can provide the means of defining all hydraulic constraints relevant to the optimal management of ground-water supplies as linear functions of the discharge decision variables. The extent to which such an approach can be used to accurately identify the hydraulic response of an aquifer system to induced pumpage depends, of course, on the degree of linearity and stationarity of the associated flow regime.
Figure 1--Coupling of simulation and optimization algorithms.
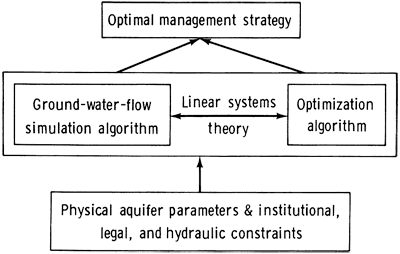
The coupling of simulation and optimization models can be performed by including a physically based flow or solute-transport simulation model as a set of constraints in a linear- or nonlinear-programming optimization algorithm. Linkage between simulation and optimization components is most easily implemented by linearizing the equations governing ground-water flow or solute-transport such that the resulting constraints are linear, because such constraints are much simpler to satisfy than nonlinear constraints. The use of coupled simulation and optimization models offers significant advantages over the usual simulation approach of defining optimal management policy through trial-and-error procedures, because the "best" policy is not a function of highly subjective judgments associated with defining potentially optimal strategies as input to a purely simulative model. Coupled simulation -optimization models implicitly minimize economic costs or maximize economic benefits of withdrawing ground water over a continuum of feasible pumpages in accordance with the hydraulic characteristics of the aquifer under investigation.
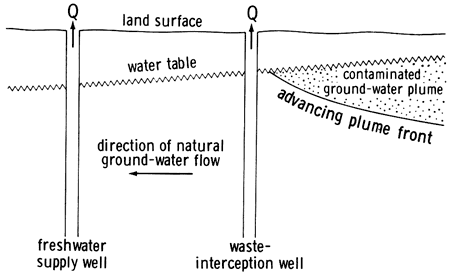
This particular investigation focuses upon identifying the economic consequences of withdrawing finite ground-water supplies from a shallow, hypothetical, unconfined aquifer subject to localized contamination. The demonstrative ground-water hydraulic management model that was formulated and executed during the course of this study is to be extended and applied to identify the optimal waste-containment strategy for the unconfined Equus Beds aquifer in south-central Kansas, where the adverse effects of short-term disposal of oil-field brines near the city of Burrton are becoming evident in the form of an extensive, but areally isolated, plume of contaminated ground water (Sophocleous, 1984). Because of the localized nature of the pollution problem in the Equus Beds aquifer, the demonstrative brine-containment strategy was formulated using a network of interception wells along the front of an advancing brine plume in a hypothetical aquifer (fig. 2). The objective of the demonstrative study was to identify optimal interception-well discharge schedules that locally reverse both natural hydraulic gradients and hydraulic gradients induced by supply-well pumping, at selected points between the interception-well network and the supply wells. Local reversal of hydraulic gradients permitted development of a ridge between fresh and contaminated ground-water supplies, resulting in a natural barrier to ground-water flow from contaminated to uncontaminated portions of the aquifer. Pollutant containment with respect to freshwater supplies was incorporated into the management strategy using ground-water velocity constraints. Horizontal ground-water movement in the hypothetical aquifer was assumed to be induced by pumpage from freshwater supply wells and from waste-water interception wells located along the advancing front of the hypothetical brine plume. Optimal supply- and interception -well discharge schedules were defined using a minimum pumping-cost approach to reflect the true cost of implementing the containment strategy. The assimilative capacity of the hypothetical aquifer through dispersive and diffusive mechanisms was assumed to not be sufficient to warrant a 'hands-off' policy towards groundwater-quality management. This assumption can be tested for a given aquifer by simulating the extent of brine dilution using overestimates of supply-well discharges and a solute-transport model. In the event that the brine concentration falls below a specified standard in the vicinity of the supply wells, the containment strategy clearly would not be justified, and a 'do-nothing' strategy clearly would represent a minimum-cost management option.
Figure 2--Waste-interception strategy.
Formulation of the demonstrative optimization model was directed towards minimizing the costs associated with pumping freshwater supply wells and waste-water interception wells in a locally polluted aquifer. All wells were operated in such a way to ensure that further movement of the contaminated plume of ground water toward freshwater supplies could be neutralized or reversed throughout the planning period. Waste-interception wells were required to pump enough ground water to stagnate flow at selected points between the interception wells and the supply wells. If the advective mechanism of pollutant transport is assumed to be dominant, flow stagnation will be equivalent to containment of wastes with respect to freshwater supplies. Brine would be representative of a solute for which advection would be the primary transport mechanism, especially for small hydraulic gradients when mechanical dispersion would tend to be negligible. The concentration of brine also was assumed to be sufficiently small to further justify the assumption of horizontal ground-water flow. For situations in which density variations between contaminated and uncontaminated ground water are significant, addressing the issue of vertical ground-water flow induced by these density variations is necessary.
Constraints used to define the minimum cost of operating the interception-supply-well network included institutional limits on minimum targeted freshwater demands and legal limits on maximum ground-water appropriations at freshwater supply wells, as well as hydraulic constraints on ground-water velocity at observation wells situated between the contaminated and uncontaminated portions of the hypothetical aquifer. In addition, hydraulic constraints on drawdown at all supply and interception wells were used to incorporate a "conservation" component to the management strategy. Mass and energy-continuity considerations were indirectly included in the operating-cost objective function and in the drawdown and velocity constraints through use of discrete unit response functions obtained from the flow-simulation component of the coupled management model.
The simulation component of the ground-water hydraulic management model was coupled with a quadratic-programming algorithm by means of a response-function approach, which served to express the hydraulic variables of a hypothetical aquifer as linear functions of the groundwater-discharge decision variables. In addition to permitting linearization of the constraints, the use of linear systems theory greatly facilitated formulation of the cost-objective function. The response-function method has successfully been used to maximize ground-water-withdrawal rates in the Pawnee Valley in south-central Kansas, subject to linearized drawdown constraint functions (Heidari, 1982a, b). For this particular study, both drawdown and velocity were described as linear combinations of a set of controllable discharge decision variables.
The drawdown algebraic technological function (Maddock, 1972)
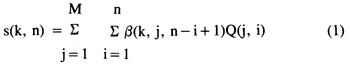
where s(k,n) = drawdown at pumping well k at the end of the nth pumping period, averaged over the finite-difference cell associated with well k [L]
β(k, j, n - i + 1) = average drawdown response of the kth well at the end of the nth pumping period to a unit pulse of pumping at the ith well during the ith pumping period [T/L2]
Q (j,i) = the average volumetric rate of discharge at the ith pumping well during the ith pumping period [L3/T]
can formally be viewed as discrete convolutions of discharge series at each pumping well with the associated unit drawdown response function β(k, j, i) summed over all M pumping wells. The time-dependent ordinates of β(k, j, i) are essentially incremental drawdowns at each of the discharging wells at the end of pumping period i, due to unit pulses of pumping at each discharging well applied during the first period only.
The unit drawdown response functions can be obtained by discretizing the hypothetical flow domain and by using finite-difference methods to solve the governing partial differential equation describing transient, two-dimensional, saturated ground-water flow in a nonhomogeneous, isotropic, confined aquifer for the drawdown variable using known initial and boundary conditions:
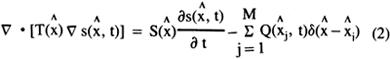
where T(![]() ) = spatially distributed transmissivity [L2/T]
) = spatially distributed transmissivity [L2/T]
s(![]() , t) = spatially distributed and time-variant drawdown [L]
, t) = spatially distributed and time-variant drawdown [L]
S(![]() ) = spatially distributed storage coefficient
) = spatially distributed storage coefficient
Q(![]() j, t) = constant rate of well discharge at vector location
j, t) = constant rate of well discharge at vector location ![]() . during time period ending at t, positive for discharge [L3/T]
. during time period ending at t, positive for discharge [L3/T]
δ (![]() -
- ![]() j) = Dirac delta function [1/L2]
j) = Dirac delta function [1/L2]
![]() = two-dimensional Cartesian space vector [L]
= two-dimensional Cartesian space vector [L]
t = time coordinate [T]
M = total number of point sinks
Areal recharge or discharge of water due to precipitation, evapotranspiration, or leakage from underlying units can be assumed to be time invariant and thus implicitly included in initial conditions defined by steady-state flow when drawdown is the independent variable. For an unconfined aquifer, the transmissivity T(![]() ) will be a function of drawdown and the equation becomes nonlinear. If the drawdown s(
) will be a function of drawdown and the equation becomes nonlinear. If the drawdown s(![]() ,t) can be assumed to be small relative to the initial saturated thickness, the system approaches linearity and time invariance, and a drawdown solution can be formulated using the principle of superposition as a linear combination of particular solutions associated with each pumping well. Moreover, if the Theis assumptions are valid, an analytical drawdown solution would exist and would be of the form:
,t) can be assumed to be small relative to the initial saturated thickness, the system approaches linearity and time invariance, and a drawdown solution can be formulated using the principle of superposition as a linear combination of particular solutions associated with each pumping well. Moreover, if the Theis assumptions are valid, an analytical drawdown solution would exist and would be of the form:
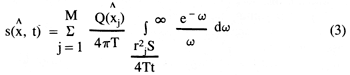
where Q(xj) = constant discharge rate at vector location xj, positive for discharge [L3/T]
S = the constant, uniform storage coefficient for the aquifer
T = the constant, uniform aquifer transmissivity [L2/T]
rj = the magnitude of the vector representing
![]() -
-![]() j[L]
j[L]
ω = dummy variable of integration.
Thus, drawdown can be expressed as a linear function of the discharge decision variables for a homogeneous, confined, infinite aquifer of constant transmissivity that is subject to horizontal, isotropic flow. Through suitable transformation of the dummy variable ω in equation (3) to a continuous analog of the time variable i, the following closed-form expression for the drawdown response coefficients can be developed for constant pumping rates within any given pumping period (Bathala, Rao, and Spooner, 1977):
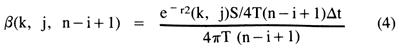
where r(k,j) = distance between pumping well j and drawdown-observation well k [L]
Δt = pumping-period duration [T]
n = index for period of observation
i = index for period during which pumping at well j begins.
Clearly, for the case in which the Theis assumptions are satisfied, the drawdown response coefficients are essentially modified forms of the well-function integrand times a scalar. However, when vertical or anisotropic flow in a finite, nonhomogeneous, unconfined aquifer is considered, equation (4) cannot be directly used to obtain the drawdown response coefficients because the drawdown solution given by equation (3) will not be valid.
For practical purposes, when the Theis assumptions cannot be justified, the unit drawdown response functions β(k, j, i) may be obtained by subjecting a calibrated finite-difference model of the flow domain to unit discharges at each pumping well for a duration of one management period utilizing known initial and boundary conditions. Corrections for radial flow may easily be incorporated into the model. Maddock (1972) proved the existence of the β(k, j, i) coefficients for a nonhomogeneous aquifer of finite extent. However, in an unconfined aquifer, the assumptions of linearity and time-invariance, which are implicit to convolution equation (1), may be violated during operation of the flow-simulation model. For the case of transient, unconfined conditions, the problems of nonlinearity and nonstationarity in the flow system become virtually inseparable because transmissivity will be a function of drawdown and this in turn will affect the stationarity of the boundary conditions.
These problems may be overcome by recalculating the drawdown responses at each time step after updating head levels in order to obtain transient response coefficients, or by correcting drawdown responses using the Jacob (1944) relationship. Alternatively, the truncated series solution to the Boussinesq equation derived by Maddock (1974b) can be used. However, given the uncertainty of determining simulation-model parameters (transmissivity T and storativity S), the problems introduced by nonlinear influences in an unconfined aquifer subject to slight transient influences can frequently be considered as insignificant potential sources of error. Moreover, the possibility of nonlinear influences for an unconfined aquifer can be reduced by assigning small maximum permissible drawdown constraints during the optimization procedure. Assumption of linearity for the unconfined case can be tested after optimization by inputting optimal Q(j,i) values to an external flow-simulation model in order to determine whether simulated drawdowns match the drawdown values predicted by the optimization model. For the unconfined case, the unit of pumpage used to obtain response functions should be sufficiently small to maintain system linearity. The velocity algebraic technological functions
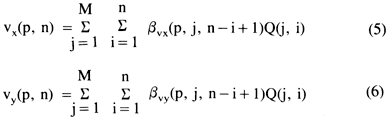
vx(p, n) = average value of x-component of velocity vector at pth velocity-observation well at end of pumping period n over associated cell [L/T]
vy(p,n) = average value of y-component of velocity vector at pth velocity-observation well at end of pumping period n over associated cell [L/T]
βvx(p, i , n - i + 1) = average velocity response in x-direction in finite-difference cell associated with pth velocity-observation well at end of nth pumping period to a unit pulse of pumping at ith well during ith pumping period [1/L2]
βvy(p, j, n - i + 1) = average velocity response in y-direction in finite-difference cell associated with pth velocity-observation well at end of nth pumping period to a unit pulse of pumping at jth well during ith pumping period [1/L2]
may be interpreted in an analogous way to the drawdown technological functions. Darcy's law supplies the means through which velocity can be expressed as linear combinations of the Q(j,i) variables. Like the drawdown response coefficients, βvx(p, j, i) and βvy(p, j, i) coefficients can be obtained by subjecting a calibrated flow-simulation model to a unit pulse of pumping at each discharge well for a duration of one management period using known initial and boundary conditions. The discrete velocity response functions defined at each velocity-observation well are then convolved with the pumping sequence at each discharging well, and these convolutions are summed over all M pumping wells according to equations (5) and (6) in order to determine the sum of incremental velocity components due to all pumping. Again, in practice the response functions must be obtained from a flow-simulation model to account for finite aquifer extent and aquifer nonhomogeneity. Considering the assumptions inherent in Darcy's law, the problem of nonlinearity again arises for transient, unconfined conditions and may affect the validity of convolution equations (5) and (6).
The ground-water hydraulic management model used during the course of the demonstrative investigation was formulated in such a way as to minimize the costs of pumping freshwater supply wells and of containing locally contaminated ground-water supplies through the simultaneous operation of interception wells located near the encroaching plume front. The cost-objective function was defined on the basis of physical factors that were believed to dominate pumping costs. Minimization of the cost function was subject to a set of institutional, hydraulic, and legal constraints related to minimum freshwater demand, maximum permissible drawdown, ground-water flow stagnation, and maximum ground-water appropriations.
Costs associated with pumping freshwater-supply wells and waste- interception wells were assumed to be directly proportional to the rate of discharge and to the total hydraulic lift at each pumping well (Nelson and Busch, 1967) . Based on this assumption, the total discounted pumping cost could be expressed as the product of a unit-cost index, the discharge at each pumping well, and the total hydraulic lift at each pumping well, summed over all pumping wells and over all pumping periods in the planning horizon. The objective function was formulated as follows (Maddock, 1972):
![]()
where Z = present value of total pumping costs for M supply and interception pumping wells over N management periods per planning period, where planning period length is equal to the sum of management period durations [$/T]
M = total number of potential supply and interception pumping wells in the aquifer at which pumping decisions are to be made
N = total number of pumping, or management, periods in the planning horizon
C(k,n) = pumping cost in future dollars per unit volume of discharge per unit total hydraulic lift at pumping well k during pumping period n [$/L4]
r = current or projected interest rate per management period
s(k,n) = average pumpage-induced drawdown over a grid cell in the center of which pumping well k is isolated at end of pumping period n [L]
L(k) = initial hydraulic lift at pumping well k [L]
Q(k,n) = average discharge rate at pumping well k during pumping period n [L3/T].
If pumping costs were to be minimized through variation of the decision variables subject to management control, objective function (7) had to be expressed as a function only of the decision variables Q(j,i) and Q(k,n), which were essentially part of the same variable set, and various fixed model parameters and constants. Substituting the unit drawdown response function given by equation (1) for the drawdown variable, the objective function was reformulated as
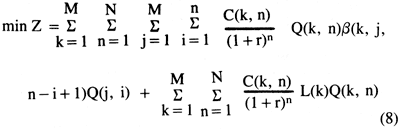
While the second term of objective function (8) is linear with respect to the discharge decision variables, the first term is a quadratic function of the discharges, and a nonlinear-programming algorithm was therefore required to identify the set of Q(k,n) variables that minimized the total cost of operating supply and interception wells in the hypothetical aquifer over a continuum of feasible pumpages. Objective function (8) permitted cost minimization over the entire planning horizon of N pumping periods. For discharge in units of cfs, lift in feet, and unit pumping cost in future dollars per cubic feet of discharge volume per total lift, minimum cost was expressed in units of present dollars per second of management-period time.
Fixed costs associated with supply-well and interception-well construction and pump installation were assumed to not be directly relevant to the optimization procedure. Use of a large number of potential sites permitted a certain degree of site-reconnaissance to be automatically performed during optimization, because operation of wells that increase pumping costs while offering no contribution towards fulfilling constraints would be assigned zero-valued discharges by the nonlinear-programming algorithm. The total cost of construction, well installation, and pumping operations can be defined on a post-optimal basis by simply adding the fixed costs at each discharging well to the cost of pumping; however, in general the resulting cost will be suboptimal because the expense of all operation and construction is not minimized. Alternatively, all possible pumping sites could be included during formulation of the management model, but such a procedure would require a prohibitive amount of computer time and storage.
Given the difficulties of introducing a site-reconnaissance element to the management model, an approach directed towards post-optimal calculations of fixed costs was adopted. This approach involved the placement of a sufficient number of supply and interception wells in critical areas of the flow domain such that the optimization procedure could assign zero-valued pumpage at those wells that contributed nothing towards satisfying the constraints at minimum cost. In effect, the number of degrees of freedom was made large enough to permit identification of a strategy which would be close to the true optimum obtained for the maximum number of potential sites in the discretized flow domain. The cost of well construction and pump installation were then determined after optimization using expected drilling and capital costs at each site for which a nonzero discharge is identified by the management model. Such a procedure does not guarantee minimum total fixed and operating costs, but it does permit water-resources planners to identify the approximate expected cost of implementing the waste-containment strategy. Costs related to disposal or treatment of wastewaters were not given consideration in the formulation of the objective function. The intercepted brine was assumed to be of sufficiently high quality to be used for certain agricultural purposes and any remaining wastewaters could be used for oil-recovery operations. Transmission costs were considered to be negligible compared to pumping costs.
Minimum Freshwater Demand--To facilitate operation of the management model, only linear constraints were used to identify the feasible region over which pumpage variables were continuously allowed to vary. A minimum target demand for freshwater supplies over the entire planning horizon was included as a constraint by introducing the equation:
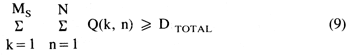
where Ms = total number of potential freshwater supply wells
DTOTAL = minimum required total rate of ground-water usage over the planning horizon of N pumping periods, considered to be deterministic and established by institutional policy [L3/T].
The above notation was used with the assumption that the first MS*N decision variables were associated with freshwater-discharge rates.
In addition, the minimum demand for fresh ground water during each pumping period was included as a subset of constraint equations such that variations in projected minimum demands between pumping periods could be introduced to the optimization procedure:
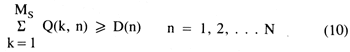
where D(n) = projected minimum demand for pumping period n, assumed to be a deterministic variable established by institutional policy [L3/T].
Maximum Permissible Drawdown--In order to incorporate a "conservation" component to the management strategy, the drawdown at all supply and interception wells for all pumping periods was constrained to be less than some fraction γ of the initial saturated thickness at the corresponding pumping well:
![]()
with b(k) equal to the initial saturated thickness at pumping well k. Equation (1) was used to transform the drawdown variables s(k,n) into linear functions of the Q(j,i) decision variables. These were incorporated into the set of linear constraint equations according to the following form:
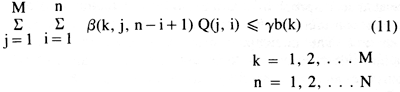
γ was chosen subjectively as a measure of the degree of conservation and was not treated as a decision variable during the optimization procedure. For unconfined conditions, γ should be chosen such that transmissivity remains roughly constant throughout the planning horizon at each pumping well and thus over the entire aquifer. In practice, the value of γ that maintains linearity under unconfined conditions is probl e m -dependent and also is subject to institutional controls.
Ground-water containment--Complete containment of the brine plume relative to freshwater supplies also was considered to be a constraint on the minimum cost of managing a freshwater-aquifer supply in the presence of contaminating influences. Pumpages at the waste-interception wells were required to neutralize or reverse the flux of water at observation wells situated ahead of the approaching front of the pollutant plume, in order to achieve the desired strategy of complete stabilization or reversal of the plume relative to the freshwater well fields. A schematic representation of the relationship between supply, interception, and observation wells, and velocity at observation wells is shown in fig. 3 in map view.
Figure 3--Schematic representation of natural and pumpage-induced velocity components.
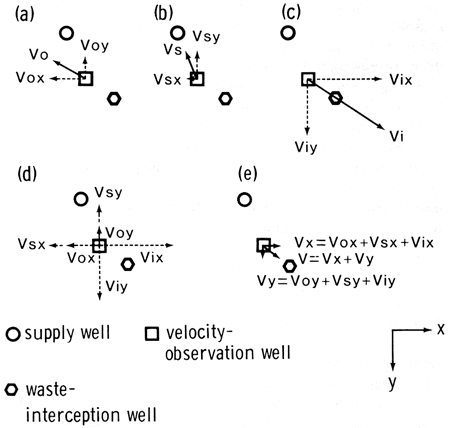
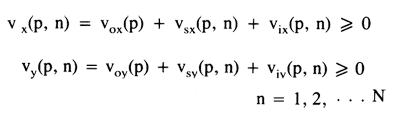
where p equals 1 for the single observation well situation. The vector component additions and the resultant vector v are shown in figs. 3d and 3e. Containment requirements must be satisfied for all pumping periods in the planning horizon.
For a system governed by steady-state initial conditions with M potential pumping supply and interception wells and Mo velocity-observation wells, the above containment constraints can be redefined in terms of the decision variables using equations (5) and (6), which essentially superimpose, or add, incremental velocity components induced by pumping:
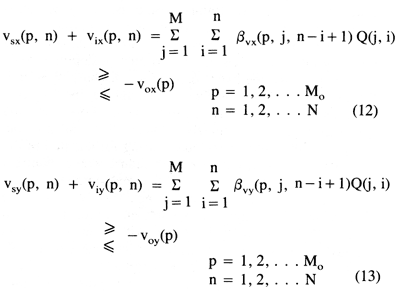
The directions of the inequality signs in inequality constraints (12) and (13) are related to the given well configuration, the location of the observation wells relative to the waste-disposal area, and the sign of negative steady-state velocity components and are entirely problem-dependent. The above constraints state that the sum of all supply-well and interception-well induced-velocity increments had to neutralize or reverse the initial, steady-state velocity components at all observation wells and for all pumping periods. A velocity neutralization approach towards containment was used rather than the more conventional approach of hydraulic head reversal in order to account for velocity anisotropy introduced by spatially variable transmissivity. The success of the containment strategy is dependent on the coarseness of the finite-difference grid used to discretize the flow domain. Flow stagnation at each observation well would more likely imply stagnation between observation wells if the wells are closely spaced, as would be the case for a fine-grid discretization.
Appropriation and non-negativity bounds--In addition to constraints (9) through (13), an upper bound was included for each supply well and for each pumping period for situations in which ground-water usage would be subject to the doctrine of prior appropriation. Appropriation constraints would be of the form:
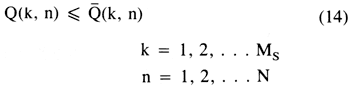
where Q(k, n) = appropriated right at supply well k during pumping period n [L3/T].
Again the decision variables would be assumed to be ordered such that the first MS*N variables are associated with freshwater supply wells. No appropriation limits were established at the interception wells, because the containment of potentially hazardous wastes was considered to have priority over all other aspects of ground-water management.
Finally, because discharge was treated as a positive variable for the interception-well containment strategy, the non-negativity constraints
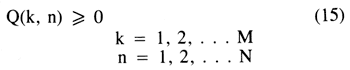
were imposed. This prevented injection from occurring at any of the M = Ms + M, potential supply or interception wells during any time in the planning period and also fulfilled the conditions required for application of the simplex method.
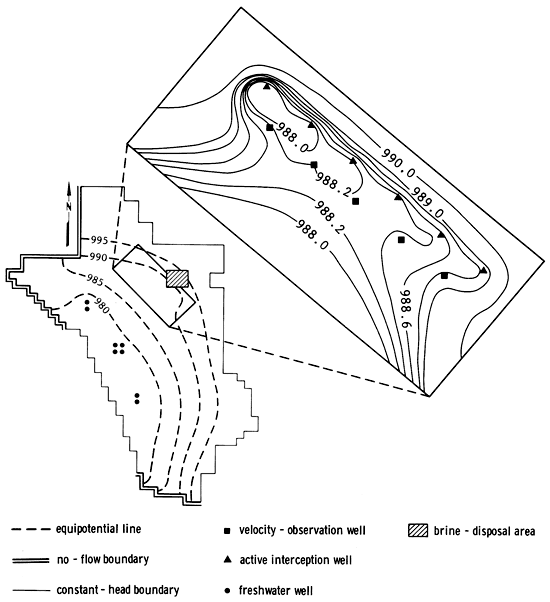
The problem of brine-containment was addressed for the hypothetical aquifer shown in fig. 4. The flow domain was discretized using a 0.5-mi nodal spacing, resulting in 49 rows and 41 columns of nodal locations and 816 active and constant-head nodes at which the aquifer was permeable. Four transmissivity zones shown in fig. 4 were assigned to the flow domain. Precipitation recharge, evapotranspiration, and leakage were assumed to be time-invariant and were therefore already accounted for in the steady-state head distribution. A uniform bedrock elevation of 0.0 ft was assigned to the hypothetical aquifer, and a land-surface elevation of 1010.0 feet was chosen for each pumping-well node in the grid as a reference for initial hydraulic-lift calculations.
Figure 4--Discretized hypothetical flow domain with transmissivity zones.
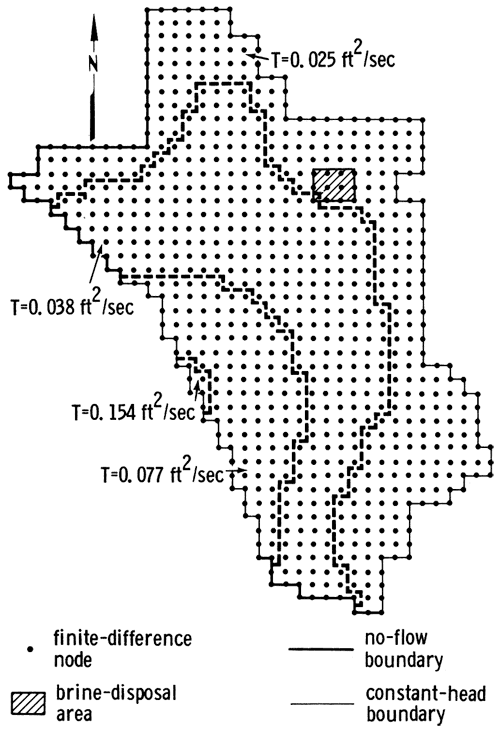
In an effort to test the ability of the optimization model to contain localized wastes in the presence of adverse steady-state hydraulic gradients, boundary conditions were chosen in such a way that a slight regional head differential was imposed on the flow regime. This involved assigning constant-head conditions of 1000 ft at all nodes located along most of the northern boundary and along the entire eastern boundary of the grid, and constant-head conditions of 975 ft along part of the western boundary (see fig. 4). All other permeable nodes were assigned arbitrary starting heads. No-flow boundary conditions were imposed at the northwestern and southern boundaries. In order to force instantaneous steady-state conditions in the flow domain, a storage coefficient of zero was assigned to each node in the finite-difference grid. Two-dimensional, steady-state flow in the nonhomogeneous aquifer was simulated using the ADI option of the finite-difference model developed by Trescott, Pinder, and Larson (1976) with 0.01-ft head error closure. The contoured steady-state piezometric head distribution and the associated initial, steady-state velocity field prior to the application of remedial containment efforts are shown in figs. 5 and 6. The hydraulic-head differential imposed by the constant-head conditions caused ground water to flow from northeast to southwest and, in the absence of pumping near the brine-disposal area, pollutants would eventually be advected into the vicinity of the freshwater well fields. The steady-state head distribution shown in fig. 5 was used to define initial conditions for the linearized aquifer system upon which the effects of pumping were imposed for five 1-yr pumping periods that would constitute the planning horizon.
Figure 5--Steady-state head distribution for hypothetical aquifer (ft).
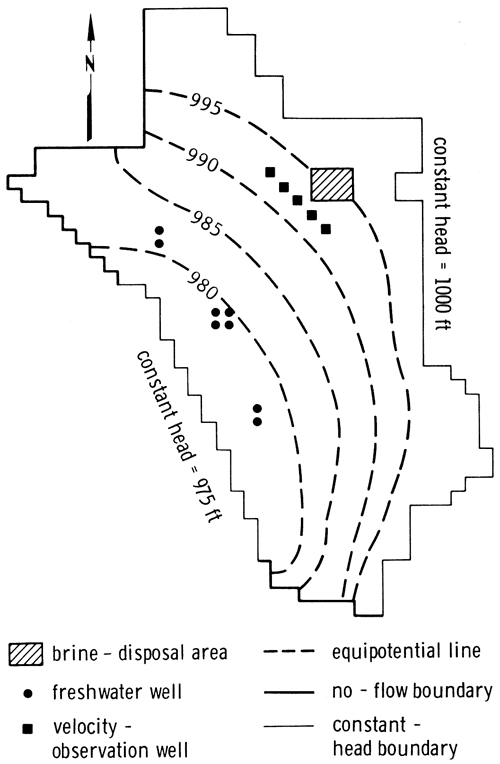
Figure 6--Initial steady-state ground-water velocity field; arrows show direction of ground-water flow.
Streamlines oriented perpendicular to the steady-state equipotential lines passing through the brine-disposal area must pass through the velocity observation well arc before reaching the supply-well fields. Thus, creation of a local ridge along the observation well arc would be sufficient to prevent contamination of freshwater supplies, given sufficiently closely spaced observation wells.
The well network used to test the suitability of applying the formulated management model to define the optimal pumping strategy is shown in fig. 7. Three supply-well fields were located in the southwestern part of the grid. Placement of the freshwater supply wells in the areas of higher transmissivity reflected a realistic management strategy.
Figure 7--Well locations.
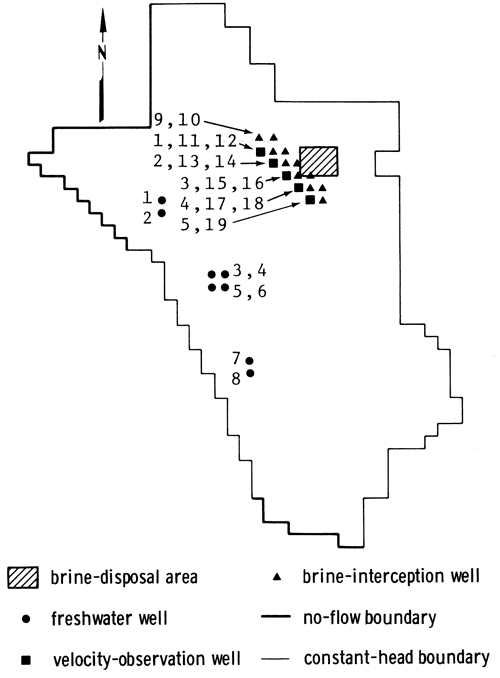
In order to test the feasibility of locally reversing a regional gradient, the brine-disposal area was placed upgradient from the freshwater supply fields. Eleven interception wells were placed along an arc corresponding to the assumed plume-front location just southwest of the brine-disposal area. Note that the supply and interception wells were numbered according to the same set of indices. The introduction of such a large number of interception wells was believed to allow a certain degree of interception-well site reconnaissance to be performed by the optimization model, which would assign zero-valued discharges to interception-well sites not required to fulfill velocity constraints at nearby observation wells at minimum cost. Five velocity-observation wells, at which velocity was to be neutralized or reversed, were situated along another arc to the southwest of the interception well network and numbered according to a separate set of indices than the pumping wells. From fig. 7, the interception wells can be seen to have been placed in such a way as to ensure adequate control on the x- and y-velocity components at all velocity-observation wells.
Ordinates of the discrete drawdown response function β(k, j, i) were obtained using a two-dimensional ADI iterative scheme developed by one of the authors (Maddock, 1974a; personal communication, 1982). Steady-state head levels (zero drawdowns) represented initial flow conditions. The transmissivity distribution and boundary conditions used to generate steady-state head values were maintained throughout the operation of the response simulation model. To account for the transient effects induced by pumpage, a uniform storage coefficient S of 0.10 was assigned to each active node in the finite-difference mesh. Porosity, which was required for purposes of defining seepage velocity, was set equal to the storage coefficient to reflect flow conditions in an undeformable medium for an incompressible fluid, characteristics of unconfined flow. Closure for the iterative model was chosen to be 0.1 ft during simulation. No attempt was made to correct drawdown for radial flow.
β(k, j, i) response coefficients for each pumping well were calculated by subjecting each pumping well to 1 ft3/sec of discharge for the duration of a 1-yr pumping period. This unit of discharge was a convenient reference for the discharge decision variables and was believed to be sufficiently small to maintain system linearity in the unconfined aquifer. Induced incremental drawdown resulting from each single pumping pulse was recorded at the discharging well, as well as at all other 18 pumping wells, for each of the five 1-yr pumping periods in the planning horizon - Then head levels were reset to initial steady-state levels, and the next pumping well was subjected to a 1-yr pulse pumping of 1 ft3/sec. This process continued until the residual drawdown effects at all 19 pumping wells due to unit pumping at each of the other 18 wells were recorded in the form of β(k, j, i) coefficients for all five pumping periods, where j was the index of the pumping well undergoing discharge, k was the index for the pumping well at which the incremental drawdown occurred, and i represented the pumping period index. The discrete response functions defined by the β(k, j, i) coefficients were subsequently lagged by one pumping period to account for the discrete nature of the convolutions inherent to objective function (8) and to drawdown constraint inequalities (11). In general, β(k, j, i) coefficients did not equal β(j, k, i) coefficients because of the nonhomogeneity and boundary conditions of the hypothetical aquifer. Inclusion of a "capture" term in any of the technological functions was unnecessary because the boundary conditions remained unchanged during the simulation.
Using the lagged coefficients, constraint inequalities (11) were expressed in matrix form. Table 1 lists the values of b(k) for all 19 pumping wells. A γ value of 0.10 was chosen as a purely subjective measure of the desired level of conservation in the unconfined aquifer, representing the maximum permissible fraction of dewatered initial saturated thickness. Given the extremely large initial saturated thicknesses at the pumping wells, this value of γ was considered to be sufficiently small to maintain linearity in the unconfined aquifer.
Table 1--Initial saturated thickness at pumping wells (ft).
| Pumping well index (k) |
b(k) |
|---|---|
| 1 | 982.40 |
| 2 | 981-09 |
| 3 | 979.14 |
| 4 | 979.99 |
| 5 | 978.62 |
| 6 | 979.49 |
| 7 | 978.77 |
| 8 | 978.40 |
| 9 | 993.56 |
| 10 | 994.49 |
| 11 | 993.16 |
| 12 | 994.07 |
| 13 | 992.89 |
| 14 | 993.77 |
| 15 | 992.81 |
| 16 | 993.72 |
| 17 | 993.00 |
| 18 | 993.96 |
| 19 | 993.36 |
In addition to the β(k, j, i) coefficients, βvx(p, j, i) and βvy(p, i, 1) velocity-response coefficients were required for each velocity-observation well and for each pumping period in order to include velocity constraint inequalities (12) and (13). Using the same flow-simulation model, induced incremental x- and y-component velocities for each pumping period were calculated at each of the five velocity-observation wells shown in fig. 7 after successively subjecting each of the 19 pumping wells to a discharge of 1 ft3/sec for 1 yr, resetting head levels to steady-state head prior to the application of each unit pulse of pumping at each pumping well. Again, the discrete βvx(p, j, i) and βvy(p, j, i) functions were lagged by one pumping period in order to perform the discrete convolutions required by the constraint inequalities (12) and (13). Corrections for radial flow were not performed. The lagged coefficients were used to construct matrix equations for constraint inequalities given by (12) and (13). Values of -vox and -voy for each velocity-observation well are listed in table 2.
Table 2--Negative steady-state velocity components at observation wells (ft/sec).
| Observation well index (p) |
-vox(p) | -voy(p) |
|---|---|---|
| 1 | 0.90 X 10-7 | -1.38 x 10-7 |
| 2 | 0.93 x 10-7 | -1.21 X 10-7 |
| 3 | 1.18 X 10-7 | -1.09 X 10-7 |
| 4 | 1.28 x 10-7 | -1.03 x 10-7 |
| 5 | 1.44 x 10-7 | -0.96 x 10-7 |
The extremely small magnitudes of the velocity components and the velocity response function coefficients made the optimization procedure extremely sensitive to round-off errors, a problem that was avoided by multiplying both sides of all velocity constraints by a factor of 10+6.
The inequalities given by (11), (12), and (13) constituted the hydraulic constraints on the operating-cost objective function. The minimum projected freshwater demand constraints given by inequalities (9) and (10) were likewise expressed in matrix form in order to incorporate management constraints during identification of an optimal reclamation strategy. Values of DTOTAL and D(1) through D(5) used for the demonstrative model are given in table 3. Uniform yearly demands of 2.76 cfs indicated a constant projected minimum demand throughout the 5-yr planning period.
Table 3--Minimum total and yearly freshwater demand rate (ft3/sec).
| DTOTAL = 13.8 | |
|---|---|
| Pumping period index (n) |
D(n) |
| 1 | 2.76 |
| 2 | 2.76 |
| 3 | 2.76 |
| 4 | 2.76 |
| 5 | 2.76 |
Constraints given by inequalities (14) and (15) were included in the management model as upper and lower bounds on the discharge decision variables. Unlike the structural drawdown, velocity, and demand constraints, they were not explicitly included in the constraint matrix but were instead used to establish a continuous range within which the decision variables were allowed to vary. Upper appropriation limits at all supply wells were assigned values of 0.5 cfs, while lower limits on positive discharge were set to 0.0 cfs.
Cost indices C(k,n) were assigned an arbitrary value of $0.000001/ft3-ft at all pumping wells for all pumping periods, and an interest rate of 7% was used to discount costs to their present values. Cost indices and the interest rate were assumed to remain constant throughout the 5-yr planning horizon. For constant and uniform values of C(k,n), the total cost of pumping was linear with respect to unit pumping cost. Thus, variations in total cost resulting from variations in C(k,n) were easily determined after optimization.
Objective function (8), together with 151 structural constraints given by inequalities (9) through (13) and 135 appropriation and non-negativity bounds given by equalities (14) and (15), formed the cost-minimization management model through which optimal strategies for developing freshwater supplies, utilizing interception wells to prevent further ground-water contamination, were identified. The nonlinear-programming optimization algorithm MINOS (Murtaugh and Saunders, 1977) was used to minimize the quadratic objective function with respect to M*N = 95 discharge decision variables and 151 slack variables. Thus, the standard form of the linear constraint matrix was of the order 151 x 246.
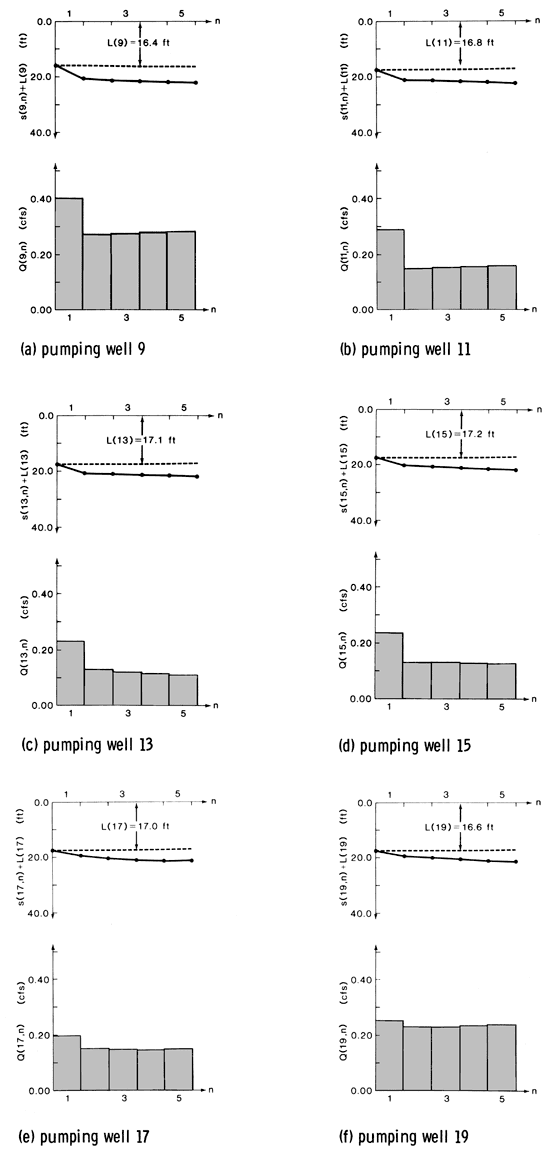
The MINOS algorithm was used to identify the optimal combination of pumping-well discharges. When the cost indices were scaled upwards to values of 0.23 $/ft3-ft, a minimum cost of 0.0005 present dollars per second of planning-period time was obtained after 153 iterations of the optimization algorithm. Execution of the optimization algorithm required 4786 seconds of CPU time on a Data General MV-8000 minicomputer. A similar version of MINOS required 860 seconds of CPU time on a Honeywell 66/60 computer when the same problem was solved. Figs. 8 and 9 show the optimal discharges at supply and interception wells that succeeded in satisfying minimum freshwater demands, maximum appropriations, maximum permissible drawdown, and complete pollutant containment at minimum operating cost. The wells located along the easternmost part of the interception-well arc, wells 10, 12, 14, 16, and 18, were not required to operate in order to neutralize or reverse the slight southwestward gradients induced by the natural flow regime or by pumping at the eight distant supply wells and were not included in the figures.
Figure 8--Optimal supply-well discharge schedules and total hydraulic lift.
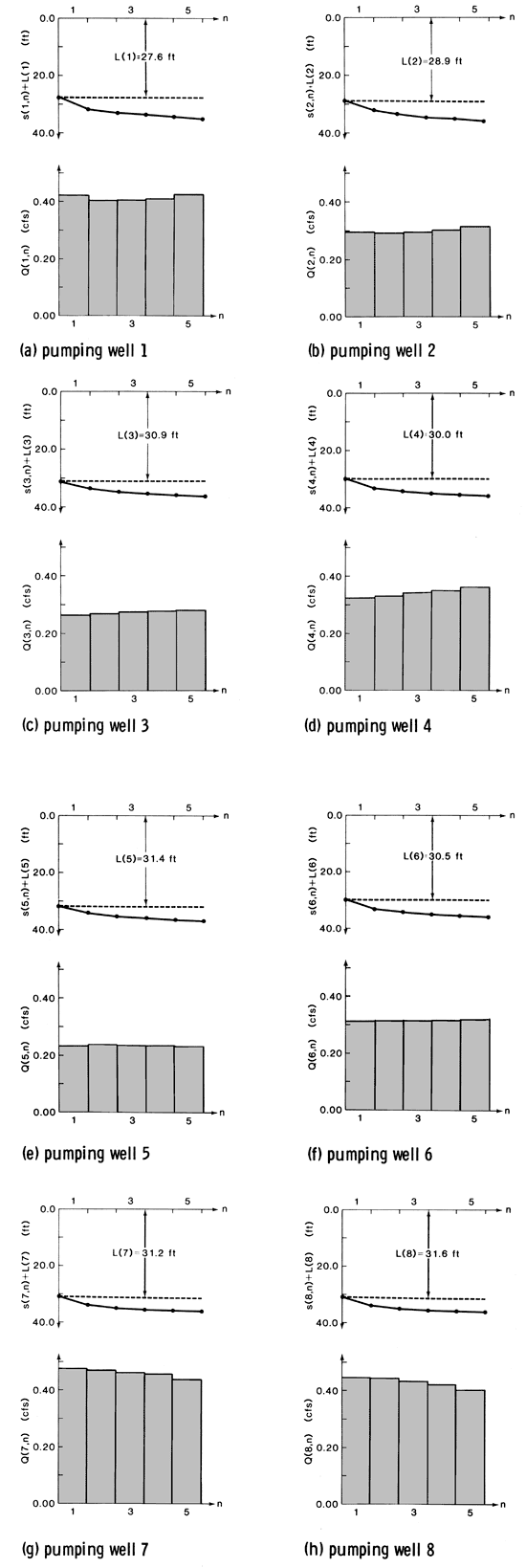
Figure 9--Optimal interception-well discharge schedules and total hydraulic lift.
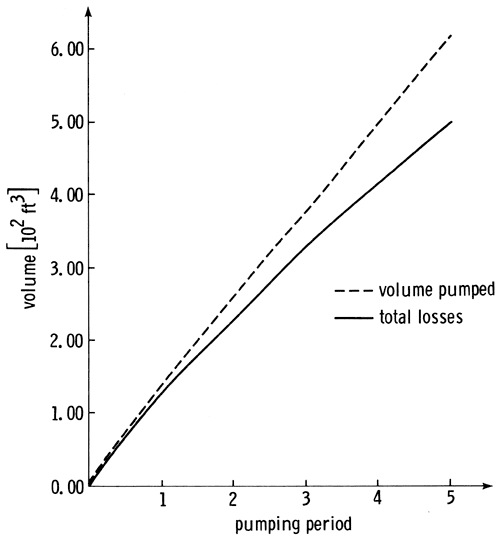
A general indication of the response of the aquifer system to optimal pumpage is shown in fig. 10, where cumulative volume of pumpage and total volume lost from storage since the beginning of pumpage are plotted. Inasmuch as the total pumpage is dominated by the larger freshwater discharge rates that are roughly constant throughout the 5yr planning period, the cumulative volume of pumped ground water is represented by a straight line. Total storage losses resulting from this pumpage, however, become progressively smaller than the cumulative volume pumped, suggesting that more ground water was obtained from the boundary sources as total withdrawal increased. The larger cumulative pumping stresses associated with increasing time apparently caused an increase in boundary contributions, especially as the effects of pumping were gradually propagated to the constant-head boundaries. Steady-state conditions clearly had not yet been attained on a regional scale by the fifth year.
Figure 10--Cumulative volume of pumpage and total storage losses.
The optimal discharge schedules for all supply and operative interception wells were input back into the finite-difference model used to obtain the response functions, after the model was suitably modified to account for non-unit pumpage rates, and the head distribution after 5 yrs was generated (fig. 11). A ridge in the equipotential surface showed an area of flow stagnation in the vicinity of the velocity-observation wells.
Figure 11--Final head distribution after 5 yrs of containment.
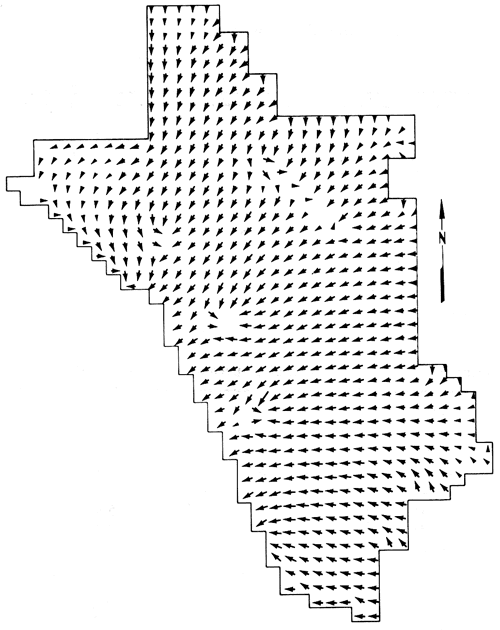
Steady-state conditions were locally attained within the first three or four pumping periods at the pumping wells, as indicated by the corresponding drawdown plots in figs. 8 and 9. Velocity fields for each of the five pumping periods are shown in figs. 12 through 16. The velocity fields illustrate that southwestward movement of contaminated ground water near the velocity-observation wells was locally neutralized immediately after the first pumping period, and that the ridge of flow stagnation along the observation-well arc was maintained during the remaining pumping periods, in accordance with the imposed velocity constraints during each pumping period.
Figure 12--Velocity field after pumping period 1; arrows show direction of ground-water flow.
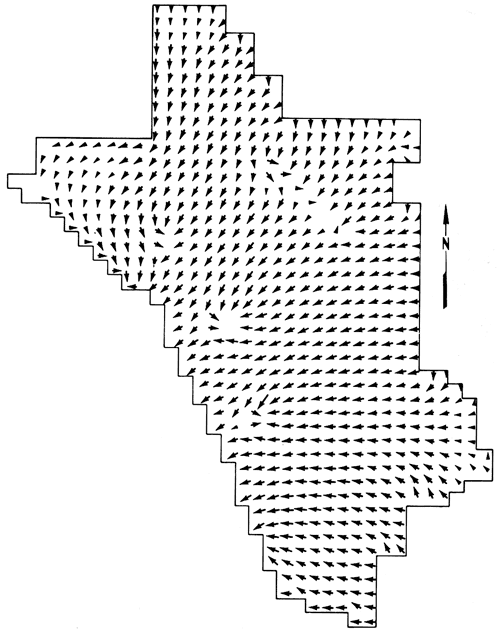
Figure 13--Velocity field after pumping period 2; arrows show direction of ground-water flow.
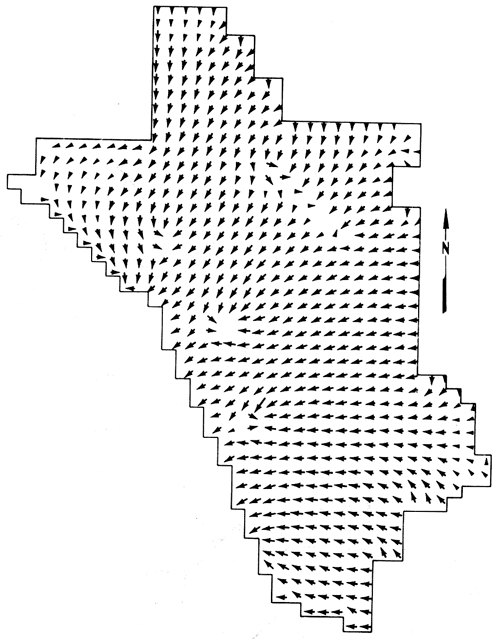
Figure 14--Velocity field after pumping period 3; arrows show direction of ground-water flow.
Figure 15--Velocity field after pumping period 4; arrows show direction of ground-water flow.
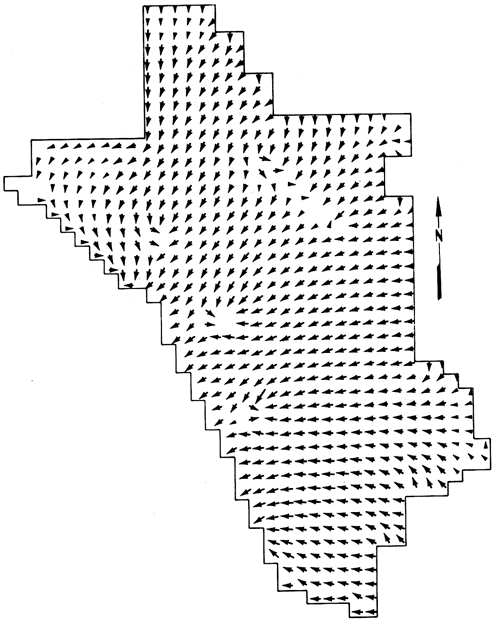
Figure 16--Velocity field after pumping period 5; arrows show direction of ground-water flow.
The optimal supply-well pumping schedules were a reflection of changing hydraulic and economic conditions that occurred throughout the planning period. These changes could generally be related to the effects of boundary conditions, variations of total hydraulic lift, and changes in the present worth of operating dollars with respect to time. The supply-well schedules and associated hydraulic lift variations shown in fig. 8 indicate that optimal discharges at the supply wells were approximately constant throughout the planning period, and that drawdown at each supply well reflected approximate steady-state conditions in the hypothetical aquifer at the end of the 5-yr planning period in the vicinity of the supply wells.
From fig. 8, the largest optimal discharges can be seen to have occurred at supply wells 1, 7, and 8. The large Q(j,i) values at supply wells 7 and 8 were attributed to large constant-head boundary contributions to these wells and to the fact that they were farther from the 0.038 ft2/sec transmissivity zone than other supply wells, which resulted in significant influx of water to these wells. These contributions effectively dampened the increase in pumpage-induced hydraulic lift at supply wells 7 and 8, permitting these wells to be pumped intensively with little increase in cost throughout the 5-yr planning period. The small increases in pumpage-induced drawdown appeared to more than compensate for the initially high lifts at these supply wells, resulting in more intensive pumping than at other supply wells. These drawdown increases, however, apparently offset the cost-discounting influence, which assigns smaller costs to later units of discharge and which would tend to produce larger optimal values of Q(j,i) over time in the absence of significant changes in the total lift at pumping wells.
Large discharges at supply well 1 were primarily attributed to the initially small lift of 27.6 ft at the well. Despite the influence of the northwestern no-flow boundary, the total hydraulic lift at supply well 1 was consistently smaller than lifts at all other supply wells throughout the planning period. Thus, the cost of pumping from well 1 was always smaller than costs incurred at most other supply wells, and more pumpage was permitted at this well. The discount influence appears to have become a factor during the final pumping period, when discharge increased slightly under roughly steady-state conditions observed at the well.
In general, optimal pumpages at the interception wells were smaller than optimal supply-well discharges (fig. 9). During the first pumping period, interception-well discharges were as large as some supply-well discharges because the velocity constraints at the adjacent observation wells had to be abruptly satisfied. This was especially evident for interception well 9, which introduced the only control on the large -voy(1) velocity constraint of -1.4 x 10-7 ft/sec at velocity-observation well 1. Thereafter, the residual effects of intensive first-period pumping at all interception wells were sufficiently large to require less intensive pumping during subsequent periods. Interception well 19, which was the only control on the large -vox(5) velocity constraint of +1.4 x 10-7 ft/sec at velocity-observation well 5, was not required to pump as much as interception well 9 despite the same magnitude of velocity-constraint vectors because slight adverse velocity influences induced by supply-well operations were more dominant at interception well 9.
The minimum cost associated with operating the pumping wells according to the indicated discharge schedules was equal to $0.0005 per second of management-period time. This value represented the sum of minimum costs associated with each pumping period and was roughly equivalent to $15,770 over the entire planning horizon, expressed in current dollars. The contribution of the linear term in objective function (8) at the optimal solution was $0.00043/sec, indicating that dynamic, nonlinear influences of increasing drawdown during pumping were small compared to the static, linear influence of the initial lifts at each pumping well. That is, more costs were incurred in overcoming the initial lift throughout the planning period than were incurred in overcoming the additional drawdowns caused by pumping. This was related to the small pumpages required to fulfill minimum freshwater target demands and neutralize or reverse slight natural and induced hydraulic gradients. These small pumpages produced small drawdowns at the pumping wells which were clearly dominated by the corresponding initial lifts, as illustrated in figs. 8 and 9.
Objective function (8) is strictly convex and the structural linear constraints given by equations (9) to (13) are, by definition, both concave and convex. This situation ensured that the necessary and sufficient conditions for a global optimum were present. The local minimum cost of $0.0005/sec was therefore a global minimum over the entire feasible region of the decision variable space (Wu and Coppins, 1981). Assuming that the eight supply wells were already constructed and that costs of well construction and pump installation can be as high as $10,000 per well, the total fixed and operating costs for the six-interception-well reclamation strategy in the hypothetical aquifer could be as large as $75,770 for the 5-yr planning period.
The dual activities, or shadow prices, of the slack variables corresponding to active demand and velocity constraints at the minimum of the cost objective function are listed in table 4. Drawdown constraints remained inactive throughout the planning period because of the small pumpage rates required to fulfill minimum supply demands and velocity constraints, and because of large drawdown limits γb(k) at the pumping wells (see table 1). Thus, minimum cost was insensitive to small changes in the drawdown constraints; the dual activities of the drawdown constraints, which reflect the changes in minimum cost per unit increase in maximum permissible drawdown, were equal to zero. Drawdown dual activities were therefore not included in table 4. The dual activities associated with a number of inactive velocity constraints also were equal to zero and are not listed in the table. For the active demand and velocity constraints listed in table 4, the dual activities, λ, represent the marginal worth of ground water, either forfeited or pumped, when the constraint corresponding to the associated demand or velocity requirement is relaxed or tightened by an infinitesimal amount. These dual activities are a direct indication of the sensitivity of minimum cost to changes in the feasible region and are invaluable aids for identification of the costs associated with satisfying a particular constraint. The variable signs associated with the values of λ for the velocity constraints were related to the sign convention used to describe the velocity vectors. Large absolute values of λ in table 4 indicate that large additional expenditures were incurred in order to fulfill the corresponding constraint, or that large savings could have been accrued if the constraint were relaxed, and suggested that an alternative means of satisfying the constraint may be more economically expedient. For the case of the velocity constraints, an alternative approach for fulfilling these constraints could involve the use of injection wells to the west and south of the velocity-observation wells for purposes of creating a barrier to westward ground-water flow.
Table 4--Dual activities of slack variables corresponding to active constraints.
| (a) | |
| Demand constraint | λ(10-5$/ft3) |
|---|---|
| DTOTAL | 2.8 |
| D(1) | 3.7 |
| D(2) | 3.5 |
| D(3) | 3.3 |
| D(4) | 3.1 |
| D(5) | 2.8 |
| (b) | ||
| Velocity constraint | Pumping period | λ(10-11$/ft) |
|---|---|---|
| voy(1) | 1 | -5.0 |
| voy(1) | 2 | -4.3 |
| voy(1) | 3 | -4.1 |
| voy(1) | 4 | -3.9 |
| voy(1) | 5 | -6.7 |
| voy(2) | 1 | -0.7 |
| voy(2) | 2 | -0.4 |
| voy(2) | 3 | -0.5 |
| voy(2) | 4 | -0.5 |
| voy(2) | 5 | -0.6 |
| voy(3) | 1 | -6.1 |
| voy(3) | 2 | 1.3 |
| voy(3) | 2 | -7.6 |
| voy(3) | 3 | 1.2 |
| voy(3) | 3 | -7.2 |
| voy(3) | 4 | 1.1 |
| voy(3) | 4 | -6.6 |
| voy(3) | 5 | 0.9 |
| voy(3) | 5 | -8.7 |
| voy(4) | 1 | 2.2 |
| voy(4) | 1 | -5.9 |
| voy(4) | 2 | 3.1 |
| voy(4) | 3 | 2.9 |
| voy(4) | 4 | 2.7 |
| voy(4) | 5 | 2.8 |
| voy(5) | 1 | 2.4 |
| voy(5) | 2 | 1.8 |
| voy(5) | 3 | 1.7 |
| voy(5) | 4 | 1.7 |
| voy(5) | 5 | 1.9 |
From table 4, the marginal worth of an infinitesimal unit of ground water used to satisfy the total 5-yr minimum freshwater demand DTOTAL can be seen to be equal to the marginal worth of a unit of ground water used to fulfill yearly freshwater demand during the final management period, D(5). The dual variable for the DTOTAL constraint, which was not explicitly included in the management model due to degeneracy considerations, was determined by means of a separate execution of the model. The DTOTAL constraint was of the form

Thus, the DTOTAL constraint equation can be derived from the yearly demand constraint equations and was not an independent constraint, a situation which resulted in a singular basis matrix and a degenerate solution. Degeneracy of the solution was avoided during the separate execution by eliminating the D(5) constraint from consideration.
Equality of the dual variables for an artificially introduced total-demand constraint and for the fifth yearly demand constraint suggested that, if additional fresh ground-water supplies were needed at minimum cost, the water should be pumped during the final management period when the present value of money is at its lowest. The decrease in dual activities for successive yearly minimum demand constraints should be noted to also have been predominantly due to discounting effects under roughly steady-state conditions observed at the pumping wells, a situation resulting in smaller present values of later pumping costs.
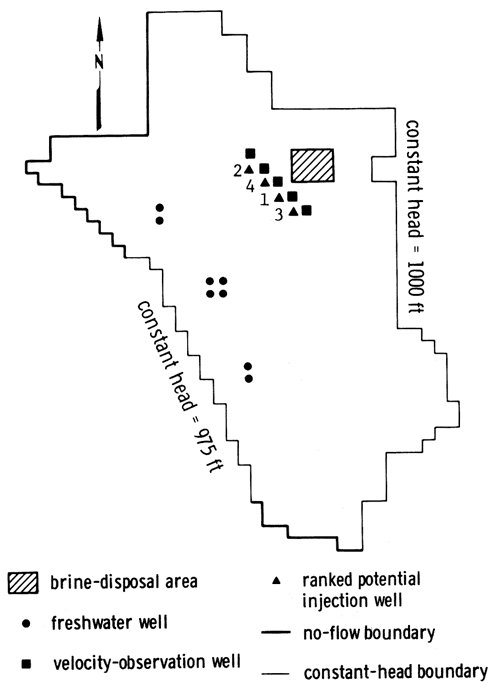
Dual activities for the velocity constraints were used to judge the marginal costs of satisfying the velocity constraints at each observation well through the interception-well strategy. Fig. 17 shows the location and the ranking of possible injection-well sites with respect to potential savings they would incur. The injection well which would offer the largest benefit ranked as I and the remaining wells were ranked in ascending order according to their potential benefits. The ranking was performed by weighing the advantages of introducing various injection wells, solely on the basis of the dual activities listed in table 4. No injection well was required to the west of velocity-observation well 1 or to the south of velocity-observation well 5 because the -vox(1) and -voy(5) constraints were inactive under the original management strategy. That is, the optimal pumping strategy required to fulfill other constraints caused the -vox(1) and -voy(5) constraints to be more than satisfied.
Figure 17--Potential injection sites.
The drawdown and velocity constraint-variable activities recorded by MINOS reflected the hydraulic behavior of a perfectly linear, time-invariant flow system. To test the validity of the assumption of linearity, the optimal pumping schedules shown in figs. 8 and 9 were used to generate drawdowns and velocity components at all discharging-well and observation-well nodes using the simulation model. Simulated drawdown and velocity components were compared to the drawdown and velocity values generated during optimization by calculating absolute normalized errors for drawdown at all supply and interception wells and velocity at all observation wells. These normalized errors were defined to be equal to the absolute values of optimal activities minus the simulated response, divided by the simulated response. Determination of normalized errors permitted drawdown and velocity errors to be compared. Table 5 lists the mean and standard deviation for the absolute values of normalized errors.
Table 5--Mean and standard deviation for absolute values of normalized drawdown and velocity errors †.
| Variable | Mean | Standard Deviation |
|---|---|---|
| Drawdown | 0.003 | 0.007 |
| x-component velocity | 0.600 | 1.339 |
| y-component velocity | 0.666 | 1.439 |
| † Mean = [(Optimal activity - Simulated response) ÷ Simulated response] | ||
Comparison of mean absolute normalized drawdown errors and mean absolute normalized velocity errors indicated that simulated velocity components were in much greater error than simulated drawdowns. This can be related to the fact that simulated velocities are a function of drawdowns at two adjacent nodal points due to the first-order spatial derivative term contained in Darcy's law. Thus, moderate errors in drawdown at two adjacent nodes will tend to produce large errors in calculated velocity. Moreover, drawdown errors generate distortions in the cross sectional flow area term, causing errors in calculated velocities to be further compounded. The larger standard deviations for the absolute normalized velocity errors can be attributed to the error magnification and dispersion associated with using Darcy's law in conjunction with simulated drawdowns which are in error. The 60% and 67% mean standardized errors associated with the x- and y-component velocities were related to the frequent occurrence of standardized errors of 1.0, which resulted when zero-valued optimal velocities were compared to very small, but non-zero, simulated velocities.
Table 6 lists minimum and maximum values for the unnormalized velocity errors. For the case of the x-component velocity, the negative minimum error suggested that, given an optimal x-component vector always oriented towards the east in the positive x-direction or of zero magnitude, the simulated vector also would be directed towards the east and would have a greater magnitude. Thus, protection of freshwater supplies was still ensured, despite possible simulation or optimization round-off error. When one considers that the minimum error component is almost two orders of magnitude smaller than the smallest steady-state x-component velocity vector, clearly the error was insignificant relative to the dynamic response of the aquifer.
Table 6--Minimum and maximum velocity errors †.
| Variable | εmin | εmax |
|---|---|---|
| x-component velocity | -0.4 x 10-1 | 0.00 |
| y-component velocity | -0.3 x 10-1 | 0.00 |
| †ε = Optimal activity - Simulated response [ft/sec] | ||
For the case of y-component velocity, optimal vectors are always oriented towards the north in the negative y-direction or are of zero magnitude. Thus, the negative minimum error vectors indicated that simulated velocity vectors were of smaller magnitude and oriented towards the north, or oriented towards the south, and that optimization round-off errors may prevent freshwater supplies from being protected according to the optimal strategy. Again, however, the minimum error component was two orders of magnitude smaller than the smallest steady-state y-component velocity, and the errors could be the result of round-off errors.
Much of the problem of velocity simulation error can be attributed to the extremely small ground-water velocities that characterized the flow regime during the planning period. Simulated velocities were quite sensitive to limitations in the accuracy of fixed-point arithmetic during execution of the external flow simulation model. Thus, the discrepancies between simulated velocity and optimal velocity components may, in fact, be primarily the result of numerical inaccuracies associated with the simulation process itself and not the product of an inaccurate optimization technique.
The management period duration required to eliminate the brine or to reduce brine concentrations to some acceptable limit may be determined by inputting optimal discharges to a solute-transport model after optimization. If brine concentrations are not below the specified limit by the end of the planning period, the management model may be executed using a longer planning period.
Linear systems theory as a mechanism for coupling the hydraulic behavior of an aquifer with the economic implications of managing this behavior is an invaluable tool for identifying optimal management strategies in freshwater aquifers that are subject to localized contamination. However, the assumption of linearity that is inherent to such an approach must be validated during post-optimality analysis by inputting optimal discharges and recharges to an external flow-simulation model. Drawdown and velocity variables generated by the quadratic -programming component of the ground-water hydraulic management model can be compared to the simulated drawdowns and velocity components. This is especially important for cases in which large maximum drawdowns are allowed. For this investigation, simulated and optimal drawdowns and velocities matched closely, given the probable extent of optimization and simulation round-off error, implying that the initial assumption was valid.
The minimum cost of implementing the proposed waste-containment strategy for the hypothetical aquifer was deter- mined to be roughly 15,770 present dollars over the 5-yr planning period. When overestimated costs of constructing operative interception wells were included, the maximum possible fixed and operating costs were estimated to be 75,770 present dollars, assuming that all interception wells would be constructed prior to the end of the first year such that cost discounting is not a factor.
The authors wish to thank Drs. Marios Sophocleous and Marian Kemblowski, staff of the Kansas Geological Survey, and Professor Yun-Sheng Yu of the Civil Engineering Department of the University of Kansas for their critical reviews of this paper. Their criticisms and contributions have hopefully made this manuscript a better product. We also would like to extend our gratitude to Kaye Long and Maria Adkins-Heljeson for contributing their typing and editing skills towards the preparation of this report. We wish to also express our appreciation to Ouarda Drici, Graduate Research Assistant at The University of Kansas, who contributed to the successful execution of flow-simulation and quadratic-programming models on The University of Kansas Honeywell Series 66/60 computer system prior to transfer of the models to the Kansas Geological Survey Data General MV-8000 computer.
Bathala, C. T., Rao, A. R., and Spooner, J., 1977, Application of linear systems analysis to ground-water evaluation studies: Purdue University, Water Resources Research Center, Technical Report No. 91, 128 p.
Gorelick, S. M., 1983, A review of distributed parameter ground-water management modeling methods: Water Resources Research, v. 19, no. 2, p. 305-319.
Heidari, M., 1982a, Application of linear system's theory and linear programming to ground-water management in Kansas: Water Resources Bulletin, v. 18, no. 6, p. 1,003-1,012.
Heidari, M., 1982b, Ground-water management options for the Pawnee Valley of south-central Kansas: Kansas Geological Survey, Ground-water Series 4, 56 p.
Jacob, C. V., 1944, Notes on determining permeability by pumping tests under water-table conditions: U.S. Geological Survey, Mimeograph Report, 25 p.Maddock, T., III, 1972, Algebraic technological function from a simulation model: Water Resources Research, v. 8, no. 1, p. 129-134.
Maddock, T., III, 1974a, A program to compute aquifer response coefficients: U.S. Geological Survey, Open-file Report 75-612, 43 p-
Maddock, T., III, 1974b, Nonlinear technological functions for aquifers whose transmissivities vary with drawdown: Water Resources Research, v. 10, no. 4, p. 877-881.
Murtagh, B. A., and Saunders, M. A., 1977, MINOS--A large-scale nonlinear programming system: Stanford University, Department of Operations Research, Systems Optimization Laboratory Technical Report SOL 77-9, 127 p.
Nelson, A. G., and Busch, C. D., 1967, Costs of pumping water in central Arizona: Arizona Agricultural Experiment Station, Technical Bulletin 182, p. 1-44.
Sophocleous, M. S., 1984, Ground-water-flow parameter estimation and quality modeling of the Equus Beds aquifer in Kansas, U.S.A.: Journal of Hydrology, v. 69, p. 197-222.
Trescott, P. C., Pinder, G. F., and Larson, S. P., 1976, Finite-difference model for aquifer simulation in two dimensions with results of numerical experiments: U.S. Geological Survey, Techniques of Water-Resources Investigations, Book 7, Chapter C1, 116 p.
Wu, N., and Coppins, R., 1981, Linear programming and extensions: New York, McGraw-Hill, 475 p.
Kansas Geological Survey, Ground-water-management options in a contaminated aquifer
Placed on web Sept. 7, 2010; originally published in 1985.
Comments to webadmin@kgs.ku.edu
The URL for this page is http://www.kgs.ku.edu/Publications/Bulletins/GW8/index.html