Kansas Geological Survey, Bulletin 233, p. 431-447
by
David M. Bice
Carleton College
The carbonate platform depositional system is sensitive to many variables, a number of which are interrelated, making it difficult to clarify how each variable affects the growth pattern of a carbonate platform. A simple computer model that simulates the carbonate platform depositional system provides an efficient means of overcoming this problem. Individual variables, such as rates of sediment production and erosion, subsidence, and eustatic sea-level cycles, are changed progressively, whereas all other variables are held constant. Changes in relative sea level (a combination of oscillatory eustatic changes, tectonic subsidence, and sediment loading) appear to exert the strongest control on the growth of carbonate platforms by determining how much sediment can accumulate on the platform top, which to some degree (along with the rate of sediment removal) influences how much sediment is available for progradation of the platform. This quantitative forward-modeling approach provides a valuable learning tool and facilitates a precise understanding of a complicated system. A forward model, such as the one presented here, can provide a basis for creating an inverse model, which can be used to constrain the variables (sediment production rate, subsidence curve, and sea-level history) that led to the cross-sectional geometry observed in the field or in a seismic section.
An Acrobat PDF file containing the complete paper is available (1.2 MB).
Beginning with Darwin (1842), geologists have sought to determine what factors control the growth patterns of carbonate platforms. Earlier studies made substantial qualitative progress [e.g., Davis (1928), Wilson (1975), Adey et al. (1977), Schlager (1981), and Kendall and Schlager (1981)]. More recent studies illustrate how computer simulations enable a more quantitative answer (Bice, 1986, 1988; Burton et al., 1987; Spencer and Demicco, 1989; Bosence and Waltham, 1990). The purpose here is to expand on the earlier model of Bice (1988), which shows how simple two-dimensional forward modeling of the carbonate platform system can facilitate the understanding of how different variables control the growth patterns of carbonate platforms and thus their internal facies architecture.
Numerous researchers (Wilson, 1975; Adey, 1978; Kendall and Schlager, 1981; Read, 1982, 1985; James and Mountjoy, 1983) have identified the various factors that influence the development of carbonate platforms. The most important factors appear to be eustatic sea-level changes and crustal subsidence, followed by such parameters as rates of sediment production and removal; types of organisms present; presence or absence of marginal rims; height and angle of marginal slopes; temperature, salinity, and clarity of water; wave energy; and supply of nutrients. These factors or variables constitute the input parameters that somehow determine whether a carbonate platform will prograde, aggrade, retrograde, or drown. These different responses, or growth patterns, in turn control the distribution of different facies or the internal stratigraphic geometry of the carbonate platform.
Because the carbonate platform depositional system is sensitive to so many variables, a number of which are interrelated, it is difficult to come to a precise understanding of how each variable affects the growth pattern of a carbonate platform. This difficulty also limits our ability to interpret correctly the geologic history that is recorded in ancient carbonate platform sediments. The simulation model of the carbonate platform depositional system presented here provides an efficient means of overcoming this problem. Individual variables can be changed progressively while all other variables are held constant, providing a precise quantitative understanding of how each particular variable influences the development of the carbonate platform system.
The model simulates a highly simplified basin that consists of three basic elements: a horizontal platform top residing in shallow water, an abrupt transition to a marginal slope, and a deep-water basin. These three basic topographic elements change their dimensions through time according to the growth pattern of the system. The platform top is assumed to be the primary source of sediment for this depositional system, supplying sediment to both the marginal slope and the basin. The slope and the basin also receive a minor amount of sediment from pelagic sources, such as calcareous and siliceous plankton. To simplify the model, I assume that the platform and basin system is isolated from any significant source of terrigenous sediment, as is the case in the modern Bahamas or in the Adriatic promontory of the Jurassic and Cretaceous (Bice and Stewart, 1990).
Some kind of nucleus is needed to initiate a carbonate platform. This nucleus can be a preexisting basement irregularity, such as a horst, or simply a point on a gentle ramp where the environmental conditions enable a dramatic increase in the rate of carbonate production. Both kinds of nucleus are present in the geologic record (Wilson, 1975; Bosellini, 1984; James and Mountjoy, 1983; Mullins, 1983) and, despite their differences, have the same function: initiating the platform and basin system. The model basin used here has a fault block nucleus, similar to the Triassic platforms of the Dolomites (Bosellini, 1984).
To facilitate computational speed, this model makes the simplifying assumption that the slope angle remains constant through time. Bosellini (1984) showed that this assumption is valid for some of the Triassic carbonate buildups in the Dolomites, where the marginal slope deposits, or clinoforms, are particularly well exposed. A more realistic yet computationally intensive method of determining the angle and form of the marginal slope is discussed by Bosence and Waltham (1990).
One of the fundamental principles of carbonate sedimentology is that the production of carbonate sediment is predominantly a biochemical process that operates most efficiently in warm, clear marine water with enough sunlight to allow photosynthesis (Wilson, 1975). The benthonic nature of most carbonate-producing organisms further requires that these conditions be met at the sediment surface. Both water temperature and sunlight decrease with increasing water depth, and it can be assumed that in a given locality there is relatively little change in the water clarity. Given these variations, it is clear that the rate of carbonate sediment production must in some way be a function of water depth. Unfortunately, there is relatively little information from modern carbonate environments that documents how the sediment production rate varies with water depth, but Smith (1972), Adey et al. (1977), and Wilson (1975) indicate that the rate of carbonate production does indeed decrease with increasing water depth, but only after remaining relatively constant down to water depths of 5-15 m (16-50 ft). The idea that carbonate production rates are most closely controlled by sunlight is supported by Wells's (1957) data for Bikini atoll. Wells showed that the number of species of hermatypic corals (among the most important contributors to carbonate sediment) dropped off according to a curve similar in form to that of solar radiance but quite distinct from the curves for oxygen and temperature change with water depth. Also with respect to corals, Buddemeier and Kinzie (1976) compared growth rates with depth and showed that within the upper 10-15 m (30-50 ft) of water growth rates tend to remain relatively constant but drop off sharply below this depth.
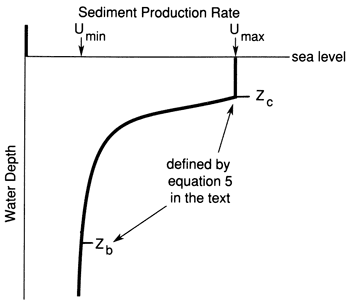
Figure 1--Relationship between sediment production rate and water depth used in the model. Umax is the maximum rate of sediment production, Umin is the pelagic rate, Zc is the depth at which the rate begins to drop, and Zb is the depth at which the rate drops to the pelagic rate. Note that, when the platform is exposed, the production rate is 0, which is equivalent to no subaerial erosion during exposure; a negative value would correspond to subaerial erosion, which is considered in fig. 9.

The model discussed here uses a sediment production function based on these observations, namely, that the rate of carbonate sediment production remains relatively constant down to a certain water depth, where it drops off rapidly at first and then more slowly at greater depths until it reaches a constant background rate. Thus the function used here is composed of four parts (fig. 1). Three parts of this function involve water depths where the sediment production rates are constant; these can be mathematically expressed in the form
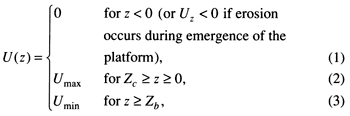
where U(z) is the sediment production rate at a given water depth z (negative above sea level, positive below), Umax and Umin are the maximum and minimum production rates, respectively (Umin is essentially the pelagic sedimentation rate), Zc is the water depth at which the sediment production rate begins to drop off, and Zb is the water depth at which the production rate drops to the pelagic rate. The fourth part of the sediment production function handles water depths between Zc and Zb, where the decrease in the production rate is constrained to be similar in form to the decrease of solar radiance in water, which has the general form
S = S0 exp(-αz) (4)
(Tyler and Preisendorfer, 1962), where S is the solar radiance (flux per unit area), a is the coefficient of attenuation of light, which is sensitive to the water clarity, z is the water depth, and S0 is the radiance at the surface. This general equation is modified to produce an exponential curve that connects the other parts of the sediment production function described by Eqs. (2) and (3), leading to the expression
U(Z) = Umax - C1{1 - exp[-λ(z - Zc)]}, (5)
where C1 is a constant for an individual model simulation, defined as
C1 = (Umax - Umin) / {1 - exp[-λ(Zb - ZC)] } (6)
and λ is a constant (usually kept at 1) that is equivalent to the coefficient of attenuation in Eq. (4). These variables and the resulting sediment production rate are shown in fig. 1. Examination of Eq. (5) shows that U(z) is essentially an exponential curve, with water depth as the independent variable and sediment production rate as the dependent variable. Note that at z = Zc Eq. (5) reduces to U(Z) = Umax and that at z = Zb Eq. (5) reduces to U(z) = Umin. In most of the experiments shown here, Umax is of the order of 1 km/m.y. (0.6 mi/m.y.) [see summary of rates by Tucker and Wright (1990)], Umin is of the order of 20-40 m/m.y. (66-130 ft/m.y.) (see summary of rates by Scholle et al. (1983)], Zc is 10 m (33 ft), and Zb is 60 m (200 ft) [both depths can be varied, but these are taken from Schlager (1981)].
It should be stressed that the sediment production function defined by Eqs. (1)-(3) and (5) is simply a mathematical expression of the observations from the modern environment. One limitation of this function arises from the possibility that the modern carbonate environment may not be a good analogy for the geologic past, especially considering the variation in communities of carbonate-producing organisms in the past (Heckel, 1974; James, 1983). This variation in carbonate-producing organisms undoubtedly alters the Umax and Umin terms but also probably alters the general form of the curve because each community of organisms responds differently to the conditions in the water column.
Cisne et al. (1984) used a slightly different depth-dependent sediment production function, choosing to make the sediment production rate gradually approach 0 as the water depth approaches 0. In contrast, the function used here involves an abrupt drop in the production rate at a water depth of 0. The particular function adopted in this study is consistent with Scatterday's (1977) observations of modern coral reefs in the Caribbean, which grow close enough to mean sea level that they are exposed during low tides. Assuming that relative sea level is presently rising, the coral reefs could not grow to such a level if sediment production rates dropped to 0 as sea level was approached.
The rate of subaerial erosion during times of emergence can vary but is usually limited to a relatively low value [<40 m/m.y. (<130 ft/m.y.)] to reflect that most shallow-water carbonates are cemented soon after deposition and are thus more difficult to erode. The eroded material can then be transported and deposited on the marginal slopes of the platform, or it can be ignored, reflecting the possibility that it would be in solution. Spatial variations in the rate of erosion are perhaps important; they would lead to topographic irregularities that could influence the later growth of the platform, but they have not been incorporated into the model presented here.
Figure 2 shows how the sediment production function is applied to the surface profile at a given time to produce a maximum rate of sediment production, yielding a profile of the potential productivity. The sediment production function can be varied for different parts of the platform to reflect natural variations, as discussed by Bosence and Waltham (1990). In all the modeling experiments shown here, the maximum rate is specified for a belt around the platform edge; the rate of sediment production in the platform interior is then specified as a percentage of this maximum rate.
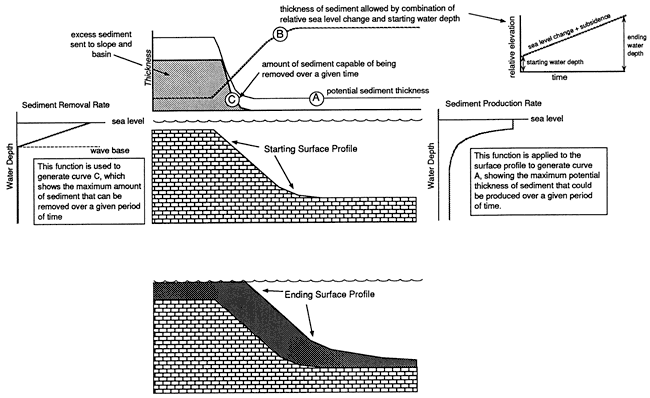
Figure 2--Calculation and distribution of the sediment budget in the model depositional system over one increment of time. At the start of each time increment, water depths across the profile are applied to the sediment production function to arrive at a maximum rate (or thickness over a given time) of sediment production for each point along the cross-sectional profile (curve A). The function for the sediment removal rate determines how much material can be transported away from the site of production (curve C). The combined starting water depth and relative sea-level change limit the amount of material that can be deposited at every point (curve B). The platform top in this figure is producing sediment faster than it can be removed; thus it can keep up with rising sea level and still produce excess sediment, which is then available for deposition on the marginal slope and in the basin. The new surface profile is the beginning profile for the next increment of time.
As pointed out by Bosence and Waltham (1990), the rate at which sediment is removed from the platform top (while submerged) is critically important to the evolution of the carbonate platform system; it effectively limits the sediment productivity of the platform. As an illustration, consider a scenario in which the rate of removal is 0. As the platform top builds up to sea level by the accumulation of sediment, the rate of production must then drop off to match the rate of relative sea-level change, thus producing no excess sediment that could accumulate on the adjacent slope and in the basin. Because the growth of the platform is strongly affected by the amount of sediment deposited on the slope, the rate of sediment removal is a key parameter.
The rate of removal used here is a linear function of water depth, ranging from a maximum just below sea level to 0 below the wave base, as shown in fig. 2. The wave base was set at 10 m (3 3 ft) below sea level in the experiments shown here, and the rate of removal was generally held constant at 0.8-1 km/m.y. [0.8-1 m/1,000 yr (2.6-3.3 ft/1,000 yr)].
Following Steckler and Watts (1978) and McKenzie (1978), the total crustal subsidence incorporated in this model is broken down into two components: (1) a tectonic or "driving" component and (2) a component contributed by sediment loading of the lithosphere. The tectonic component is a variable parameter, and the sediment loading component is a consequence of many of the other parameters in the depositional system.
Two different types of functions for the tectonic component of the subsidence--linear and nonlinear--can be used in this model. Although nonlinear time-dependent subsidence may be more realistic geologically, it is easier to interpret the model experiments in which linear subsidence is used. The forward modeling of Turcotte and Willeman (1983), Turcotte and Kenyon (1984), and Burton et al. (1987) included spatial variations in the rate of subsidence, which is consistent with observations from the Atlantic continental margin of North America (Sleep and Snell, 1976; Steckler and Watts, 1978). The model presented here forces the subsidence to be constant across the cross section because the horizontal distances of most of the cross sections generated by this model are relatively small [<10 km (<6.2 mi)] compared to the widths of most continental margins [~200 km (~120 mi)]. In addition, flexure of the lithosphere has been ignored, once again because the horizontal dimensions of the cross sections generated by this model are small with respect to the typical wavelengths of flexural displacement of the lithosphere [~100-200 km (~60-120 mi); Turcotte and Schubert, 1982].
The component of the total subsidence contributed by the sediment load is calculated by assuming an isostatically balanced system, which leads to the expression

where A is the amount of subsidence induced by the sediment load, hs is the thickness of sediment, and ρm, ρs, and ρw, are the densities of the mantle (3.3 g/cm3), sediment (2.0-2.5 g/cm3), and seawater (1.0 g/cm3), respectively.
Compaction has been ignored in the model simulations shown here. There is some evidence that shallow-water carbonates undergo little compaction because of early cementation (Bathurst, 1975), but in laboratory experiments [summarized by Tucker and Wright (1990)] variable amounts of compaction are observed. Because of these uncertainties in the compaction of carbonates, no attempt has been made to modify sediment thicknesses as they become buried, as must be done for siliciclastic sediments (Steckler and Watts, 1978; Bond and Kominz, 1984).
The use of this simple isostatic model requires the acceptance of two assumptions. The first assumption is that the crust can adjust quickly enough to the sediment load to maintain an approximate equilibrium over each increment of time for which a sediment budget is calculated and deposited. This effectively constrains the time increment to at least 10,000 years, which is the length of time required for the crust to adjust to the application or removal of a load (Cathles, 1975). The second assumption is that the thickness of the crust remains constant. However, some amount of crustal thinning is implied by the tectonic component of the subsidence, so the model used here effectively assumes that the crustal thinning occurs instantaneously between time increments. Of course, this isostatic model sacrifices some degree of realism for the sake of simplicity, but the point is that the total subsidence is a function of the amount of sediment deposited.
Adey (1978), Kendall and Schlager (1981), James and Mountjoy (1983), Hine and Steinmetz (1984), Read et al. (1986), and others have pointed out the importance of sea-level fluctuations in controlling the development of carbonate platforms. Sea-level rises allow sediments to accumulate on the tops of platforms and control the amount of excess sediment produced on the platform tops that can be deposited on the marginal slopes and in the basins. If sea level rises rapidly enough, the top of the platform may fall to water depths below the zone of high productivity, effectively shutting down the carbonate platform system, a process known as drowning (Schlager, 1981). Sea-level falls can lead to emergence of the platform top, which also shuts down the production of carbonate sediment. Clearly, sea-level changes have an important effect on the evolution of carbonate platforms by controlling the magnitude and the distribution of the sediment budget.
At this point, it is important to draw a distinction between relative sea-level changes and eustatic sea-level changes. A eustatic sea-level change is the displacement of global sea level with respect to an arbitrary datum, such as the geoid. A relative sea-level change is simply the sum of crustal subsidence and eustatic sea-level change; it is therefore the displacement of sea level relative to the basement. Because the platform top is attached to the basement, relative sea level is the most important measurement of sea level so far as the depositional environment is concerned. For example, if the local subsidence rate is greater than the eustatic rate of sea-level fall, then the carbonate platform experiences a relative sea-level rise.
Following the work of Barrell (1917), Vail et al. (1977), and others, the model presented here incorporates several frequencies of harmonic sea-level oscillations, so that the general expression for eustatic sea level is given by
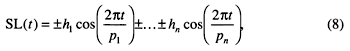
where SL(t) is the variation of eustatic sea level relative to its initial level at a given time t and hn and pn are the amplitude and the period, respectively, of each sea-level cycle. The initial slope (positive or negative) of each sea-level cycle can be controlled using the plus or minus sign, allowing a variety of composite sea-level curves.
The sea-level oscillations used in this model were designed to be symmetric, following the recent work of Haq et al. (1987). Clearly asymmetric high-frequency, glacially driven eustatic cycles (Hays et al., 1976) are not considered here because the details of such high-frequency cycles cannot be resolved by the model since the time increment of analysis (10,000 years), which cannot be reduced because of the necessity of allowing isostatic adjustment, is significant with respect to the period of these glacial cycles (20,000-100,000 years). However, the general effects of these higher-frequency fluctuations can still be understood in a relative sense by simply observing the changes produced by altering a different range of frequencies. It should be stressed that the sea-level curves used in this model are purely synthetic.
Sediment budgets are calculated and distributed throughout the model depositional system over time increments of 10,000 years to allow a simple isostatic adjustment to the sediment load. The procedure for calculating the sediment budgets is schematically shown in fig. 2. At the start of each time increment, the water depths across the platform and the basin are applied to the sediment production function to arrive at a maximum rate of sediment production for each point along the cross-sectional profile, which, over a specified length of time translates to a maximum thickness of sediment that can accumulate at each point (curve A in fig. 2). However, this potential thickness of sediment is limited by two factors: (1) the amount of sediment that can be accommodated by the combined effects of subsidence and sea-level change and (2) the rate of sediment removal (submarine) from the platform top. As illustrated in fig. 2, the change in relative sea level and the starting water depth at each point along the profile yield a curve that shows how much sediment is permitted to accumulate over a given time increment (curve B in fig. 2). The places along the profile where curve A is greater than curve B are regions that may produce an excess of sediment that could be distributed to other parts of the depositional system. The amount of excess sediment produced at each point is actually controlled by the rate of sediment removal, which varies along the profile according to curve C in fig. 2. So long as curve A (the productivity) is above curve C (rate of removal), the platform will show a net accumulation of sediment. If the difference between these two curves is greater than curve B (relative sea-level rise), then the platform will be able to keep up with a rising sea level. The total amount of excess sediment, shown by the shaded region below curve C in fig. 2, is then available for deposition on the marginal slope and in the basin, providing the potential for progradation of the platform.
The partitioning of this excess sediment budget between the marginal slope and the basin probably depends on a number of factors, including the grain size distribution of sediment produced on the platform top. For simplicity this partitioning is specified and held constant in each simulation experiment. The dispersal and deposition of the excess sediment results in a new profile of the sediment surface (fig. 2), which serves as the beginning profile for the next increment of time.
The model also contains a set of simple rules that govern the response of the carbonate platform system to varying conditions of relative sea-level change, starting water depths, and rates of sediment production, removal, and accumulation. These rules are illustrated in fig. 3, which shows a variety of scenarios that might occur over a given time increment. Because the time increments are short with respect to the periods of sea-level changes, relative sea-level changes are approximated as straight lines over each increment of time. This kind of rate analysis is performed at all points across the surface profile.
Figure 3--Response of the platform and the generation of the sediment budget under four different conditions. In each diagram the length of time is of the order of 10,000 years so that the relative sea-level curves can be approximated by a straight line. The horizontal line at the base of each diagram is the position of the platform top at the beginning of the time increment. An explanation of these four scenarios is given in the text.
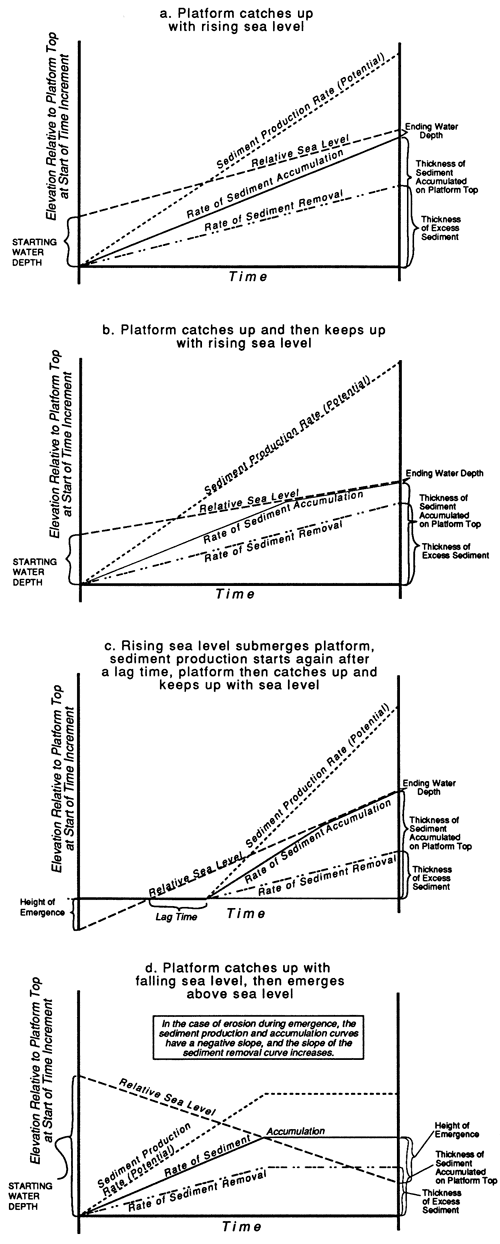
In fig. 3a the starting water depth defines a rate of sediment production and a rate of sediment removal (submarine); the difference between these defines the rate of sediment accumulation. If the rate of accumulation is greater than the rate of relative sea-level rise, the platform top will catch up to sea level. If the accumulation curve intersects the rising sea-level curve, then the rate of accumulation drops off, enabling the platform to keep up with sea level (fig. 3b). Once the platform top catches up to sea level, the rates of sediment removal and production will generally increase, enabling the platform to produce more excess sediment, which in turn enables the platform to prograde.
In fig. 3c the platform top is above sea level at the beginning of the time increment, but rising sea level eventually submerges the platform top. During emergence, the rate of sediment production is 0 (i.e., no subaerial erosion), which means that the rates of sediment accumulation and removal are also 0. Figure 3c shows a short lag time following the submergence of the platform. The lag time, as pointed out by Adey (1978), Kendall and Schlager (1981), and Schlager (1981), appears to be a function of how long it takes the community of carbonate-producing organisms to reestablish themselves on the previously emerged platform top. Based on Pleistocene and Holocene carbonate buildups from the Caribbean, Adey (1978) estimated that the lag time was of the order of 1,000-2,000 years. After the lag time, efficient carbonate production resumes but at a rate corresponding to the water depth at that time, which depends on both the rate of relative sea-level rise and the length of the lag time. In the particular case illustrated in fig. 3c, the sediment production and removal rates established at the end of the lag time enable the platform top to catch up to and then keep up with rising sea level, producing excess sediment in the process. A lag time of 1,000 years was used in the model experiments shown here, but its effect is negligible under the range of sea-level fluctuations used.
Figure 3d shows the assumed behavior of the carbonate platform during a fall in relative sea level that leads to the subaerial exposure of the platform top. Once the sediment accumulation curve intersects the falling sea-level curve, the platform emerges. If no subaerial erosion occurs, the sediment production curve flattens out, as do the accumulation and removal curves. If subaerial erosion occurs, the sediment production curve will have a negative slope, which is followed by the sediment accumulation curve; the sediment removal curve will take on a positive slope, the inverse of the production curve. In the model experiments shown here, the rates of subaerial erosion range from 0 to 40 m/m.y. (0-130 ft/m.y.), significantly less than rates of sediment production or removal, which are of the order of 1,000 m/m.y. (3,300 ft/m.y.). An important consequence of this behavior during emergence is that little excess sediment is produced, severely limiting the ability of the platform to prograde.
The effects of different parameters on the growth of carbonate platforms can be investigated by performing a series of experiments in which one parameter is systematically changed while all other inputs are held constant. The results are displayed in the form of cross sections showing a series of time lines that illustrate the evolution of the platform and the basin system and graphs of the relative elevations of sea level and the platform top through time. These graphs are particularly useful in understanding the effects of sea-level changes.
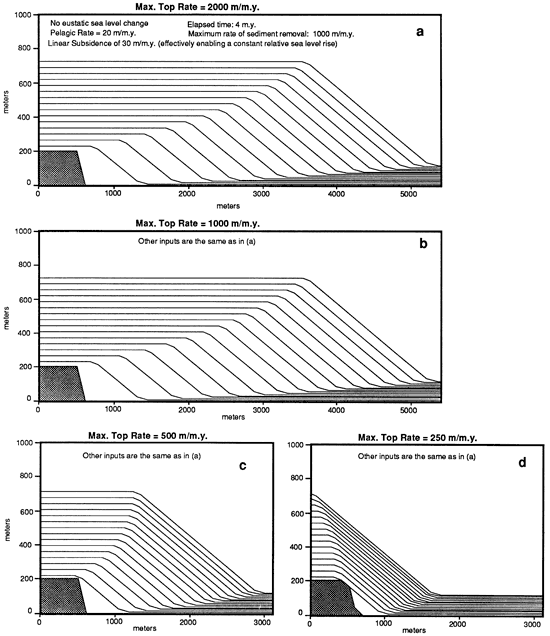
Figure 4 shows four cross sections that illustrate the effect of changing the maximum rate of sediment production (Umax) that is possible on the platform top. The experiments involve a linear subsidence history with no eustatic sea-level fluctuations. Changing the maximum production rate from 2,000 m/m.y. (6,600 ft/m.y.) to 1,000 m/m.y. (3,300 ft/m.y.) has no effect on the growth of the platform because of the limiting role of the rate of sediment removal, which was set at 1,000 m/m.y. (3,300 ft/m.y.). Under these conditions the platform is capable of producing sediment faster than it can be removed. When the maximum rate of production drops below the rate of removal, less excess sediment is generated and deposited on the marginal slope, restricting the amount of progradation that occurs. As this amount of excess sediment decreases, the platform edge retreats through time. The fact that any excess sediment is generated under the conditions shown in figs. 4c and 4d is somewhat unexpected. At shallow depths the maximum rate of sediment removal is so great that all the sediment is swept away before it can accumulate. This results in the platform top dropping to greater water depths, where the rate of sediment removal is much lower. At these greater water depths the rate of sediment production can outpace sediment removal; accumulation can occur, bringing the platform top to shallower waters until the point where the removal again outweighs the production. In this way the system evolves to a fixed depth at which the platform top can keep up with a slowly rising sea level and still produce a modest amount of excess sediment.
Figure 4--Results of a sequence of experiments showing the effect of changing the maximum rate of sediment production. These synthetic cross sections show time lines drawn at regular intervals of time; each time line is equivalent to the surface profile at that particular time. A portion of the platform nucleus, a fault block, is shown in the lower left; its true horizontal dimension in all the experiments shown is 1 km (0.6 mi). The cross sections focus on the edge of the platform and do not show the entire extent of the platform top. Variations in the maximum rate of sediment production on the platform top affect the amount of excess sediment that is necessary for progradation of the platform. However, the fact that parts a and b are identical shows that the rate of submarine sediment removal is an important limiting factor in determining this excess sediment budget.
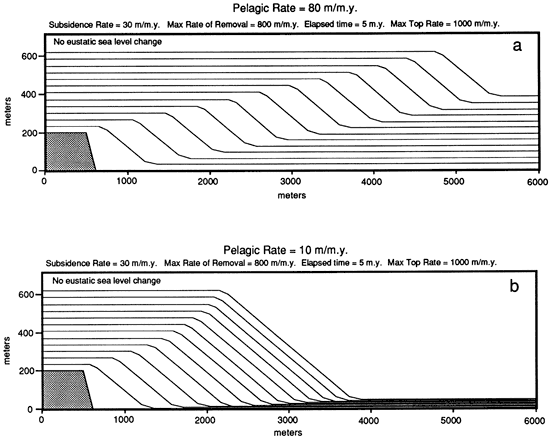
The pelagic sedimentation rate (Umin) is also capable of influencing the growth of the platform system. Figure 5 shows two cross sections created with different pelagic rates. When the pelagic rate is lower than the rate of relative sea-level rise on the platform top, the height of the platform above the basin increases through time. As a result an equal amount of excess sediment leads to thinner marginal slope deposits and less progradation. The ability of the platform to prograde is greatly enhanced with increased pelagic rates, which prevent the platform from increasing in height. This effect is even more exaggerated in experiments (not shown here) in which the whole platform top contributes excess sediment to the marginal slope. The cross sections in figs. 5 and 6 were created under the assumption that a fixed width of the platform top (representing a fringing reef complex) provides all the sediment for the slope. Experiments in which the whole platform top contributes excess sediment to the slope are characterized by occasional runaway progradation, an effect of positive feedback.
Figure 5--Sequence of experiments showing the effect of changing the rate of pelagic sedimentation. A low pelagic rate of sedimentation tends to enhance the upward growth of the platform, whereas a high pelagic rate tends to limit the amount of upward growth. As the platform grows higher, it becomes more difficult to prograde because more sediment is required to prograde a given distance.
Changing sea level Changes in sea level probably exert the most profound control on the evolution of the carbonate platform system simulated by this model. Figures 6 and 7 show a number of experiments that illustrate some of the important effects of eustatic sea-level changes; fig. 7 illustrates the importance of the combined effects of eustatic sea level and subsidence. These experiments involved only one sea-level cycle at a time to illustrate more clearly their effects on the growth of the platform system. In all these figures cross-sectional views of platforms are accompanied by graphs that show the elevations of sea level and the platform top through time relative to the top of the nucleus (shaded region in cross sections). The nucleus is part of the crust and subsides through time; thus the sea-level curve is actually the relative sea level, not the eustatic sea level.
Figure 6--The effect of first adding a single sea-level cycle to a linear rate of subsidence and then progressively increasing the period of the sea-level cycle. The cross sections are accompanied by graphs that plot the elevation of sea level and the platform top relative to the top of the nucleus. The relative sea level is shown by a solid line, and the platform top is shown by a dashed line; a single solid line is shown when the two features coincide, marking times when the platform top is just below sea level, keeping up with any changes in sea level. A comparison of these results shows that increasing the period of a sea-level cycle leads to a decrease in the amount of time that the platform is above sea level, which enhances the progradation of the platform. Also note that in part a the path formed by the position of the platform edge through time is not a straight line and thus is not a direct reflection of the relative sea-level curve. Examination of the other cross sections and their accompanying graphs shows that the relative sea-level curves are only approximately reflected by the path formed by the platform edge through time.
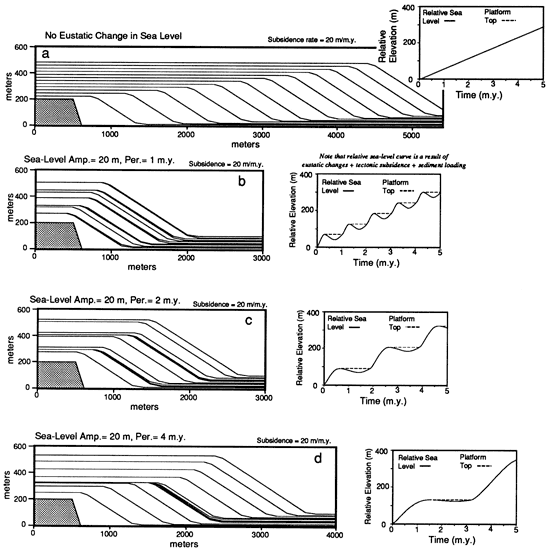
Figure 7--Sequence of experiments showing the effect of adding a sea-level fluctuation to different linear subsidence rates. In general, any sea-level fluctuation with a downward slope that exceeds the rate of tectonic subsidence will lead to emergence, which restricts the progradation of a platform. In part c the tectonic subsidence rate just exceeds the downward slope of the sea-level cycle and no emergence occurs, just a period of stillstand in sea level, during which the platform is more able to prograde.
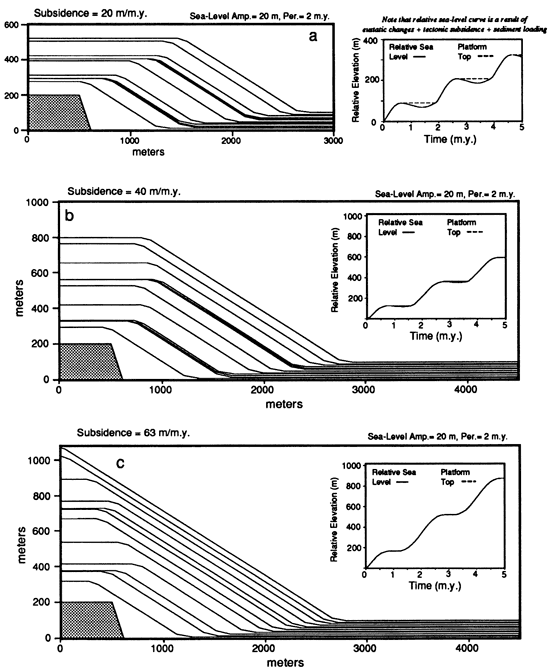
With no eustatic sea-level changes and a modest rate of subsidence [20 m/m.y. (66 ft/m.y.)], the platform in fig. 6a progrades rapidly. A dramatic change occurs, however, when a eustatic fluctuation is added (fig. 6b). The reason for this effect is seen quite clearly in the graph plotting relative sea level and the platform top. When the solid line representing sea level drops below the dashed line representing the platform top, the platform top is exposed above sea level and the carbonate production system is shut down. These periods of emergence thus reduce the excess sediment budget necessary for the platform to prograde.
The experiments shown in figs. 6b through 6d show the effect of changing the period of the sea-level fluctuation. Increasing the period enhances the progradation of the platform for two reasons: (1) It decreases the length of time that the platform top is above sea level (the total time of emergence in fig. 6d is 50% less than that in fig. 6b), and (2) it decreases the slope of relative sea-level rise, which restricts the increase in platform height that makes progradation more difficult. Times of emergence can be detected on the cross section itself by the time lines that show no sediment accumulation on the platform top and only a little accumulation on the marginal slopes. One of the obvious implications of these experiments is that the higher-order sea-level cycles, with periods of the order of 10,000 years and 100,000 years, should significantly reduce the ability of carbonate platforms to prograde because they would cause the platforms to be exposed so frequently.
Figure 8 shows the effect of changing the amplitude of the eustatic sea-level cycles. Increasing the amplitude restricts the progradation of the platform for two reasons: (1) It increases the total time of emergence, although the number of emergent periods is the same; and (2) increased amplitudes lead to greater platform heights, which inhibit progradation by reducing the thickness of marginal slope deposits produced by a given amount of sediment. A comparison of figs. 8a and 8c shows that an amplitude change of 20 m (66 ft) causes the platform to grow about 100 m (320 ft) higher. This enhancement occurs because a greater thickness of sediment results in greater total subsidence.
Figure 8--Two sets of experiments in which the period of a sea-level cycle is held constant at 2 m.y., and the amplitude is progressively increased from 10 m (33 ft) to 20 m (66 ft) to 40 m (130 ft). Increasing the amplitude of a sea-level cycle leads to greater upward growth of the platform and an increase in the duration of emergence, both of which lead to a decrease in progradation.
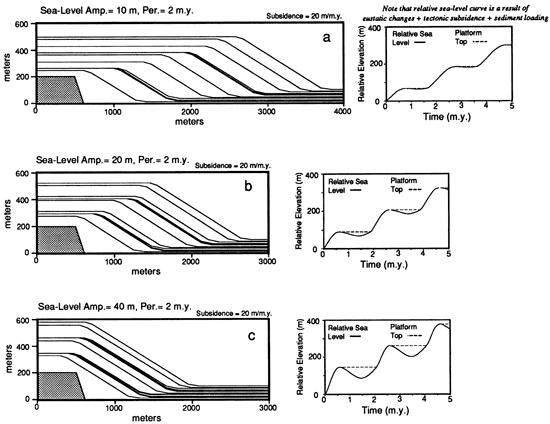
An interesting feature that can be observed in the sea-level elevation graphs in figs. 7 and 8 is the change in the slope of the relative sea-level curve that takes place as the platform is submerged following a period of subaerial exposure. This is a function of the subsidence caused by the deposition of sediment. Because no sediment is deposited on the platform top during emergence, there is no additional component of the total subsidence during these times. Only the tectonic component of the subsidence operates. But as soon as the platform is submerged, sediment accumulation begins and contributes to the total subsidence, increasing the slope of the relative sea-level curve.
The relationship between eustatic sea-level cycles and subsidence is equally important in controlling the growth of the platform system. Figure 7 shows the effect of combining a sea-level fluctuation with an increasing rate of subsidence. When subsidence is relatively low (fig. 7a), the platform is subjected to periods of emergence that restrict its progradation. As the rate of subsidence increases, the times of emergence become shorter (fig. 7b) and eventually disappear, replaced by segments of time with slight increases in relative sea level (fig. 7c). When the times of emergence disappear, the platform is actually capable of prograding more effectively than when there are no sea-level fluctuations. The change in the effect of a sea-level fluctuation from restricting progradation to enhancing progradation occurs when the total subsidence (tectonic and sediment load) exceeds the maximum downward slope of the eustatic sea level, at which point the relative sea level does not drop and the platform top does not emerge. In mathematical terms the change occurs when the sum of the two slopes (subsidence and sea level) is greater than 0. The slope or derivative of a single sea-level cycle expressed in the form of Eq. (8) is
dSL / dt = ±(2πh / p) sin(2πt / p), (9)
which has a maximum value of
dSL / dt = ±(2πh / p), (10)
For the case shown in fig. 7c, the sea-level cycle has an amplitude of 20 m (66 ft) and a period of 2 m.y., so the greatest downward slope value is -20π m/m.y. (-66π ft/m.y.), or -63 m/m.y. (-200 ft/m.y.), which is matched by the tectonic component of the subsidence, resulting in a relative stillstand in sea level.
The final set of experiments, shown in fig. 9, illustrates the role of subaerial erosion during times of exposure. The rate of erosion is varied from 0 to 40 m/m.y. (0-130 ft/m.y.), and two primary effects can be observed: (1) Higher erosion rates tend to increase slightly the amount of progradation that occurs, and (2) higher erosion rates lead to the formation of toplap geometries of the marginal slope deposits. The higher erosion rates produce only a slight increase in progradation because the entire platform top in these experiments is relatively small-the actual starting width of the nucleus is just 1 km (0.6 mi) (the cross section shows just the edge of the platform). The small size of the platform results in a relatively minor amount of sediment being deposited on the marginal slopes. A third effect of erosion during emergence can be seen by referring to the graphs plotting relative sea level and platform top elevations. Just as the weight of sediment increases the slope of relative rises in sea level, erosion or removal of material increases the slope of the relative sea-level falls, the net effect being a more asymmetric relative sea-level curve.
Figure 9--The effect of varying rates of subaerial erosion during emergence. Subaerial erosion during times of emergence leads to the development of toplap relationships and to more asymmetric relative sea-level curves. The relative low rates of erosion and the small horizontal dimension of the platform top combine to minimize the amount of progradation that occurs during times of exposure.

The forward model presented here is intended to represent a simple first-order model that enables rapid simulation of the carbonate platform and basin system. It is important to remember that, although this is a quantitative simulation technique, it by no means claims to simulate accurately all the complexities that occur in a natural system. The primary function of these simple simulations is to serve as an efficient learning tool. It enables us to observe how changing a particular variable affects the development of the carbonate platform and adjacent basin, displaying the results rapidly enough to be nearly interactive-a 5-m.y. simulation takes approximately 15 s on a Macintosh IIx computer.
The series of experiments illustrated in figs. 5 through 9 demonstrate how different variables affect the platform system. Variations in the maximum rate of sediment production on the platform top affect the amount of excess sediment necessary for progradation of the platform. However, the rate of submarine sediment removal is a limiting factor in determining this excess sediment budget. The pelagic rate of sedimentation can also affect the growth pattern of the carbonate platform system; low rates tend to enhance the upward growth of the platform, whereas high pelagic rates tend to limit the amount of upward growth. As the platform grows higher, progradation becomes more difficult because increasingly more sediment is required to prograde a given distance. Changes in relative sea level appear to exert the strongest control on the growth of carbonate platforms. In general, any sea-level fluctuation with a downward slope that exceeds the rate of tectonic subsidence will lead to emergence, which restricts the progradation of a platform. Decreasing the period of a sea-level cycle leads to an increase in times of emergence and thus a decrease in the progradation of the platform. Increasing the amplitude of a sea-level cycle leads to greater upward growth of the platform and under certain conditions an increase in the duration of emergence, both of which lead to a decrease in progradation. Subaerial erosion during emergence leads to the development of toplap relationships and to more asymmetric relative sea-level curves.
The synthetic cross sections also illustrate some of the constraints on inferences that can be made on the basis of their geometry. In many of the cross sections shown in figs. 6 through 9 the form of the relative sea-level curve is reflected in the path formed by tracing the position of the platform edge through time. This observation makes it tempting to suggest that the path of the platform edge in an ancient carbonate platform can be used to determine the relative sea-level history. However, the subsidence would still have to be separated from the eustatic sea level. A similar suggestion was made by Bosellini (1987), who proposed that the path of the platform edge is a direct image of the subsidence curve, which would be accurate only if sea level was at a standstill. Nevertheless, the results of these experiments point out at least two problems that make these inferences difficult. First, as shown in the cross section of fig. 6a, a perfectly linear rate of subsidence, even with a static sea level, results in a concave-up path of the platform edge. Second, changes in the sediment production rate on the platform top (fig. 4), the pelagic sedimentation rate (fig. 5), or the size of the source area for the marginal slope sediments can significantly alter the form of the platform edge path.
The second main function of forward models such as the one presented here is to serve as a basis for creating an inverse model, which, as pointed out by Turcotte and Kenyon (1984), could be used to calculate the variables (such as the sediment production rate, the subsidence rate, and the sea-level history) that led to the cross-sectional geometry observed in the field or in a seismic section. A major problem that must be anticipated in creating such an inverse model for the carbonate platform system is nonuniqueness; there may be many combinations of input data that lead to the same observed cross-sectional geometry. An additional problem is that forward models more sophisticated than the one presented here are a prerequisite to meaningful inverse modeling; yet the more sophisticated models would undoubtedly involve more input parameters, increasing the problem of nonuniqueness. However, it is conceivable that appropriate observations from several platforms of the same age in different areas could be used to constrain the possible input data combinations. This type of inverse modeling may eventually provide a more objective and quantitative measure of the eustatic sea-level history than is currently available.
This work benefited greatly from discussions with Walter Alvarez, Alberto Michelini, Kevin Stewart, Lung Chan, Mike Field, and Scot Krueger. I thank D. Osleger and A. Simo for thoughtful and helpful reviews. Acknowledgment is made to the donors of the Petroleum Research Fund, administered by the American Chemical Society, for partial support of this research.
Adey, W. H., 1978, Coral reef morphogenesis--a multidimensional model: Science, v. 202, p. 831-837
Adey, W. H., Maclntyre, I. G., Stuckenrath, R., and Dill, R. F., 1977, Relict barrier reef system off St. Croix--its implications with respect to late Cenozoic coral reef development in the western Atlantic: Third Coral Reef Symposium Proceedings, University of Miami, Coral Gables, Florida, v. 2, p. 15-21
Barrell, J., 1917, Rhythms and the measurement of geologic time, 2d ed.: Geological Society of America, Bulletin, v. 28, p. 745-904
Bathurst, R. G. C., 1975, Carbonate sediments and their diagenesis: 2d ed., Developments in Sedimentology 12, Elsevier, Amsterdam, 658 p.
Bice, D. M., 1986, Computer simulation of prograding and retrograding carbonate platform margins: Geological Society of America, Abstracts with Programs, v. 18, no. 6, p. 540-541
Bice, D. M., 1988, Synthetic stratigraphy of carbonate platform and basin systems: Geology, v. 16, p. 703-706
Bice, D. M., and Stewart, K. G., 1990, The formation and drowning of isolated carbonate seamounts--tectonic and ecologic controls in the northern Apennines; in, Carbonate Platforms--Facies, Sequences, and Evolution, M. E. Tucker, J. L. Wilson, P. D. Crevello, R. J. Sarg, and F. J. Read, eds.: International Association of Sedimentologists, Special Publication 9, 145-168
Bolt, B. A., 1982, Inside the earth: W. H. Freeman and Co., San Francisco, California, 191 p.
Bond, G. C., and Kominz, M. A., 1984, Construction of tectonic subsidence curves for the early Paleozoic miogeocline, southern Canadian Rocky Mountains--implications for subsidence mechanisms, age of breakup, and crustal thinning: Geological Society of America, Bulletin, v. 95, p. 155-173
Bosellini, A., 1984, Progradational geometries of carbonate platforms--examples from the Triassic of the Dolomites, northern Italy: Sedimentology, v. 3 1, p. 1-24
Bosellini, A., 1987, Dynamics of Tethyan carbonate platforms (abs.): American Association of Petroleum Geologists Bulletin, v. 71, p. 532
Bosence, D., and Waltham, D., 1990, Computer modeling the internal architecture of carbonate platforms: Geology, v. 18, p. 26-30
Buddemeier, R. W., and Kinzie, R. A., III, 1976, Coral growth: Oceanography and Marine Biology, Annual Review, v. 14, p. 183-225
Burton, R., Kendall, C. G. St. C., and Lerche, I., 1987, Out of our depth--on the impossibility of fathoming eustasy from the stratigraphic record: Earth Science Reviews, v. 24, p. 237-277
Cathles, L. M., 1975, The viscosity of the earth's mantle: Princeton University Press, Princeton, New Jersey, 386 p.
Cisne, J. L, Gildner, R. F., and Rabe, B. D., 1984, Epeiric sedimentation and sea level-synthetic ecostratigraphy: Lethaia, v. 17, p. 267-288
Darwin, C., 1842, The structure and distribution of coral reefs: Smith Elder, London, 344 p.
Davis, W. M., 1928, The coral reef problem: American Geographical Society, New York, 596 p.
Haq, B. U., Hardenbol, J., and Vail, P. R., 1987, Chronology of fluctuating sea levels since the Triassic: Science, v. 235, p. 1,156-1,167
Hays, J. D., Imbrie, J., and Shackleton, N. J., 1976, Variations in the earth's orbit-pacemaker of the ice ages: Science, v. 194, p. 1,121-1,132
Heckel, P. H., 1974, Carbonate buildups in the geologic record--a review; in, Reefs in Time and Space, L. F. Laporte, ed.: Society of Economic Paleontologists and Mineralogists, Special Publication 18, p. 90-154
Hine, A. C., and Steinmetz, J. C., 1984, Cay Sal bank, Bahamas--a partially drowned carbonate platform: Marine Geology, v. 59, p. 135-164
James, N. P., 1983, Reef environment; in, Carbonate Depositional Environments, P. A. Scholle, D. G. Bebout, and C. H. Moore, eds.: American Association of Petroleum Geologists, Memoir 33, p. 345-440
James, N. P. and Mountjoy, E. W., 1983, Shelf-slope break in fossil carbonate platforms-an overview; in, The Shelfbreak--Critical Interface on Continental Margins, D. J. Stanley and G. T. Moore, eds.: Society of Economic Paleontologists and Mineralogists, Special Publication 33, p. 189-206
Kendall, C. G. St. G., and Schlager, W., 1981, Carbonates and relative changes in sea level: Marine Geology, v. 44, p. 181-212
McKenzie, D., 1978, Some remarks on the development of sedimentary basins: Earth and Planetary Science Letters, v. 40, p. 25-32
Mullins, H. T., 1983, Structural controls of contemporary carbonate continental margins-Bahamas, Belize, Australia; in, Platform Margin and Deep Water Carbonates, H. E. Cook, A. C. Hine, and H. T. Mullins, eds.: Society of Economic Paleontologists and Mineralogists, Short Course 12, p. 2-1-2-57
Read, J. F., 1982, Carbonate platforms of passive (extensional) continental margins-types, characteristics and evolution: Tectonophysics, v. 81, p. 195-212
Read, J. F., 1985, Carbonate platform facies models: American Association of Petroleum Geologists Bulletin, v. 69, p. 1-21
Read, J. F., Grotzinger, J. P., Bova, J. A., and Koerschner, W. F., 1986, Models for generation of carbonate cycles: Geology, v. 14, p. 107-110
Scatterday, J. W., 1977, Low-water emergence of Caribbean reefs and effect of exposure on coral diversity--observations of Bonaire, Netherlands Antilles; in, Reefs and Related Carbonates--Ecology and Sedimentology, S. H. Frost, M. P. Weiss, and J. B. Saunders, eds.: American Association of Petroleum Geologists, Studies in Geology 4, p. 155-170
Schlager, W., 1981, The paradox of drowned reefs and carbonate platforms: Geological Society of America, Bulletin, v. 92, p. 197-211
Scholle, P. A., Arthur, M. A., and Ekdale, A. A., 1983, Pelagic environment; in, Carbonate Depositional Environments, P. A. Scholle, D. G. Bebout, and C. H. Moore, eds.: American Association of Petroleum Geologists, Memoir 33, p. 619-691
Sleep, N. H., and Snell, N. S., 1976, Thermal contraction and flexure of midcontinent and Atlantic marginal basins: Geophysical Journal of the Royal Astronomical Society, v. 45, p. 125-154
Smith, S. V., 1972, Production of calcium carbonate on the mainland shelf of southern California: Limnology and Oceanography, v. 17, p. 28-41
Spencer, R. J., and Demicco, R. V., 1989, Computer models of carbonate platform cycles driven by subsidence and eustasy: Geology, v. 17, p. 165-167
Steckler, M. S., and Watts, A. B., 1978, Subsidence of the Atlantic-type margins off New York: Earth and Planetary Science Letters, v.4l,p.1-13
Tucker, M. E., and Wright, V. P., 1990, Carbonate sedimentology: Blackwell Scientific Publications, Oxford, 482 p.
Turcotte, D. L., and Kenyon, P. M., 1984, Synthetic passive margin stratigraphy: American Association of Petroleum Geologists Bulletin, v. 68, p. 768-775
Turcotte, D. L., and Schubert, G., 1982, Geodynamics: John Wiley and Sons, New York, 450 p.
Turcotte, D. L., and Willemann, R. J., 1983, Synthetic cyclic stratigraphy: Earth and Planetary Science Letters, v. 63, p. 8996
Tyler, J. E., and Preisendorfer, R. W., 1962, Transmission of energy in the sea; in, The Sea, v. 1, Physical Oceanography, M. N. Hill, ed.: John Wiley and Sons, New York, p. 397-451
Vail, P. R., Mitchum, R. M., and Thompson, S., III, 1977, Seismic stratigraphy and global changes in sea level--pt. 3, relative changes of sea level from coastal onlap; in, Seismic Stratigraphy--Applications to Hydrocarbon Exploration, C. Payton, ed.: American Association of Petroleum Geologists, Memoir 26, p. 63-81
Wells, J. W., 1957, Coral reefs; in, Treatise on Marine Ecology and Paleoecology, J. W. Hedgpeth, ed.: Geological Society of America, Memoir 67, v. 1, p. 609-631
Wilson, J. L., 1975, Carbonate facies in geologic history: Springer-Verlag, New York, 471 p.
Kansas Geological Survey
Comments to webadmin@kgs.ku.edu
Web version April 23, 2010. Original publication date 1991.
URL=http://www.kgs.ku.edu/Publications/Bulletins/233/Bice/index.html