Kansas Geological Survey, Bulletin 204, part 3, originally published in 1972
Originally published in 1972 as Kansas Geological Survey Bulletin 204, part 3. This is, in general, the original text as published. The information has not been updated.
Daily discharge and conservative water quality predictions can be made for the lower Kansas River Basin with a relatively simple mathematical model suitable for use on a high speed digital computer. The model is based primarily on information available from the data acquisition network operated by the United States Geological Survey. The water quantity portion of the model has been tested for hydrologic accuracy by the reconstitution of eight observed discharge records each of 36 days duration. The water quality aspect of the model has been evaluated by comparing observed and predicted concentrations of individual dissolved ions at selected locations in the basin.
Potential uses for this type of model include evaluation of proposed reservoir operating policies on downstream water quality, investigation of the effects of irrigated agriculture on surface water resources of a region, and determination of the impact of industrial development on water quality.
Limitations and potential improvements to the model are discussed.
KEY WORDS: Water quality, Models, Hydrology, Geology.
The objective of this paper is to outline the salient parts of a water quality model of the lower portion of the Kansas River Basin. The model was developed to investigate the effect of reservoir operational policies on downstream water quality under various patterns of farming, industrial development, and population growth which might occur within the basin. The deterministic approach was used because the reservoirs involved in the study had been designed as multipurpose structures prior to development of the model. The time and space distribution of both conservative and non-conservative pollutants were included in the model (Smith, et al., 1966). Conservative pollutants are solutes which are not significantly affected by biological metabolism. Non-conservative solutes are changed in composition and concentration by aquatic biota. Only conservative pollutants will be discussed in this paper.
This investigation was supported in part by the Federal Water Pollution Control Administration under contracts PH 86-66-62 and 14-12-58 with the University of Kansas Center for Research, Inc., and in part by the University of Kansas Computation Center.
The assistance of the Kansas District Office of the United States Geological Survey, the Kansas City District Office of the United States Corps of Engineers, the Environmental Health Services Division of the Kansas State Department of Health, and the office of the Missouri-Souris-Red River Basins Comprehensive Water Pollution Control Project of the Federal Water Pollution Control Administration in obtaining the data used in the development of the model is greatly appreciated. Particular thanks in this regard are extended to Lewis A. Young and Melville W. Gray.
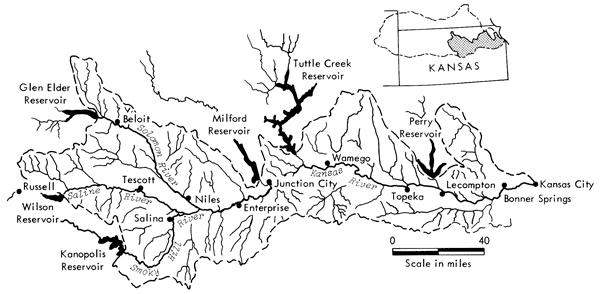
The Kansas River Basin contains approximately 60,060 square miles and lies within the states of Colorado, Nebraska, and Kansas. The rivers within the basin originate in the mountains of Colorado and the plains of western Nebraska and flow generally eastward and southward from their sources. The Kansas River is formed at the confluence of the Republican and the Smoky Hill rivers near Junction City, Kansas, and flows eastward for approximately 170 miles to join the Missouri River in the Greater Kansas City Metropolitan Area. The Republican, the Solomon, the Smoky Hill, the Saline, the Big Blue, and the Delaware rivers are the major tributaries contributing to the Kansas River. A series of reservoirs constructed or under construction on these rivers will provide a high degree of regulation for the water entering an area of approximately 8,800 square miles in the lower subbasin. The reservoirs provide a logical boundary for controlled inputs to a mathematical model. The sub-basin created in this way below the reservoirs is indicated by the shaded portion of Figure 1. Also shown in Figure 1 are the geographical locations of the principal rivers, cities, and reservoirs in the model area. The significant characteristics of the rivers and reservoirs in the sub-basin are given in Table 1.
Figure 1--Location map and physical details of the lower Kansas River Basin model area.

Table 1--Characteristics of the major rivers and reservoirs of the lower Kansas River Basin.
| River | Reservoir | Date of reservoir completion |
Conservation plus sediment storage and total storage (acre feet) |
Average annual flow before regulation (CFS) |
|---|---|---|---|---|
| Delaware | Perry | June 1969 | 290,000 770,000 |
430 |
| Big Blue | Tuttle Creek | March 1962 | 425,300 2,367,000 |
1,700 |
| Republican | Milford | June 1966 | 460,000 1,160,000 |
1,170 |
| Solomon | Glen Elder | June 1970 | 239,100 976,000 |
350 |
| Saline | Wilson | June 1965 | 265,000 775,000 |
135 |
| Smoky Hill | Kanopolis | February 1948 | 47,300 432,900* |
290 |
| *Storage in 1966 adjusted to include sediment accumulation since construction. Source: Kansas water Resources Board, Topeka, Kansas. |
||||
Approximately 40 percent of the 1970 population of Kansas was located within the model area. Industry in the region has traditionally been agriculturally oriented with production of significant quantities of wheat, corn, and beef. However, light and heavy manufacturing not tied to farming is rapidly increasing at the present time.
The general topography of the model area is of low relief. The eastern portion of the model area contains extensive areas of glacial deposits. However, the post-glacial topography has been considerably modified by erosion. The land adjacent to the major streams is highly dissected and is rough to hilly. The topography west of Topeka is more rock controlled with irregular, east-facing escarpments and considerable dissection. Some of the minor tributaries in this region have narrow steep-sided basins. However, the major streams throughout the model area have developed relatively wide valleys which are underlain by alluvium in floodplain and terrace deposits.
The average annual precipitation ranges relatively uniformly from 24 inches in the west near Russell to 36 inches in the east near Kansas City. Precipitation is most prevalent between April and September and is attributed primarily to air mass and frontal thunderstorms. These storms generally move from southwest to northeast and contribute significantly to the discharge of the rivers below the reservoirs. As shown in Table 2, approximately 37 percent of the mean annual discharge of the Smoky Hill River at Enterprise originates below the three upstream reservoirs. Similarly, approximately 40 percent of the mean annual discharge in the Kansas River at Bonner Springs originates below the six reservoirs which surround the model area (Furness, 1959).
Table 2--Summary of average annual streamflow originating within the lower Kansas River Basin model area.
| River | Station | Summation of mean annual discharge at upstream reservoir sites (CFS) |
Mean annual flow at station (CFS) |
Percentage of total flow at the station generated in model area (%) |
|---|---|---|---|---|
| Saline | Tescott | 135 | 223 | 39.5 |
| Solomon | Niles | 383 | 558 | 31.4 |
| Smoky Hill | Enterprise | 832 | 1,324 | 37.2 |
| Kansas | Wamego | 3,599 | 4,664 | 22.8 |
| Kansas | Lecompton | 3,956 | 5,850 | 32.4 |
| Kansas | Bonner Springs | 3,956 | 6,548 | 39.6 |
| Source: Kansas Water Resources Board, Topeka, Kansas. | ||||
The major influence on the conservative water quality of the Kansas River and its tributaries is the surface geology of the basin. The reservoirs which surround the study area are relatively shallow and well mixed by wind action (U.S. Corps of Engineers, 1967). These impoundments therefore act as integrators of the waters originating in the western portion of the Kansas River Basin and provide inputs to the model of relatively constant quality. The actual chemical composition of the water from each reservoir depends, of course, on the geology of the individual river basin and upon upstream uses of the water. The discharges from Kanopolis, Wilson, and Glen Elder are relatively high in total dissolved solids while those from Milford, Tuttle Creek, and Perry are low in total dissolved solids.
The chemical composition of river discharges originating below the reservoirs from overland and groundwater flow is influenced by the geology of the region in which the water originates. For purposes of water quality characterization the bedrock in the model area can conveniently be subdivided into the Pennsylvanian, Permian, and Cretaceous systems.
Cretaceous rocks are prevalent west of a line intersecting the confluence of the Solomon and Smoky Hill rivers. Although the Cretaceous System is primarily marine in origin, a significant continental deposition known as the Dakota Formation is located in this region. The Dakota Formation is composed of clayey shales, calcareous shales, chalky limestones, and sandstones, and is believed to be a principal contributor of dissolved solids. Highly saline portions of this formation contribute large quantities of chloride to the lower reaches of the Saline, Solomon, and Smoky Hill rivers, some of which may originate in deeply buried Permian strata below the Dakota Formation. Significant amounts of calcium, sulfate, and carbonate are also added to the river system from this region.
Permian rocks of late Paleozoic age dominate the surface geology in the area between the confluence of the Smoky Hill and the Solomon rivers and the Kansas River at Wamego, Kansas. These marine sedimentary rocks include sandstones, limestones, shales, and dolomites. Relatively large amounts of dissolved sulfate, calcium, and carbonate originate in this area. The addition of chloride to the river system from this area is small.
Rocks of the Pennsylvanian System, also of late Paleozoic age, crop out in the region east of Wamego. Glacial activities north of the Kansas River have resulted in the deposition of large quantities of loess and till. These loess deposits are cemented with calcium carbonate and are the principal source of this inorganic pollutant to the lower reaches of the Kansas River. Very small quantities of chloride-bearing material are also present throughout this region.
The influence of these geologic subregions on the water quality in the basin is illustrated in Table 3 which summarizes the average increase in chloride load in tons per day observed in the region prior to reservoir regulation. The numerical values given in Table 3 were computed by numerical integration of the flow duration curve for each station (Furness, 1959) with its respective equation for average chloride load as a function of discharge. The development of these average load equations will be discussed later in the paper. The apparent drop in average chloride load between Lecompton and Bonner Springs given in Table 3 is not real but simply an artifact of the integration computations.
Table 3--Summary of average chloride load originating within the lower Kansas River Basin model area.
| River | Station | Summation of average chloride load at upstream reservoir sites (tons/day) |
Average chloride load at station (tons/day) |
Percentage of total chloride load at the station generated in model area (%) |
|---|---|---|---|---|
| Saline | Tescott | 38 | 98 | 61 |
| Solomon | Niles | 40 | 79 | 49 |
| Smoky Hill | Enterprise | 189 | 480 | 61 |
| Kansas | Wamego | 308 | 601 | 49 |
| Kansas | Lecompton | 315 | 717 | 56 |
| Kansas | Bonner Springs | 315 | 700 | 55 |
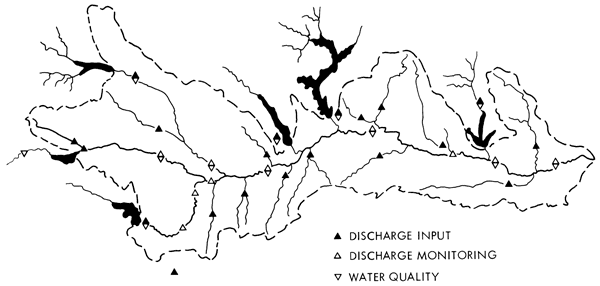
Selection of a technique for computing river discharges was dictated by the objectives of the model and the type and quantity of data available. The network of stream gaging and water quality stations shown in Figure 2 was the primary source of data for the region. All of these stations are part of the regular data gathering program of the United States Geological Survey. Little information on groundwater quality, quantity, or movement was available so this portion of the hydrologic cycle could not be isolated and treated as a separate identity in the model.
The time of flow from the western portion of the model area to the outlet of the basin at Kansas City varies from 3 to 4 weeks at average discharges to approximately 6 weeks at low flows. This factor coupled with the precipitation pattern which occurs in the region below the reservoirs produces rapid variations in discharge in the river network. A 1-day time increment was therefore considered necessary to adequately model the system. While the use of average monthly flows would simplify computer operations, this time interval would not provide a meaningful examination of either discharge or water quality.
The translation of flows downstream was accomplished by use of the hyperbolic relationship between average velocity and discharge developed by Leopold and Maddock (1953). Storage attenuation was not included in the translation procedure. This simplification limits the applicability of the model to bankfull channel discharges on the major rivers in the system. Fortunately, these are the flows of primary significance in water quality management. The model will adequately reproduce the translation of flood flows on small tributaries that are subsequently confined within the banks of the major streams. This observation is based in part on a series of dye studies (Kansas State Department of Health, 1967), and in part on the results of the hydrologic simulation studies discussed below.
The hydrologic flow pattern was simulated by starting at the western-most point in the sub-basin and adding or subtracting water as the flow proceeded downstream. Input data were inserted at the six reservoir sites surrounding the region and at 14 tributary gages shown in Figure 2. These latter gages control less than 40 percent of the land area in the model area, however, so it was necessary to synthesize daily flow inputs, termed QADDS, for the rest of the area.
Figure 2--Discharge input locations and water quality and discharge monitoring locations currently used in the lower Kansas River Basin model.
The QADDs were subdivided into (1) the contributions from ungaged tributaries which were correlated with adjacent gaged areas; (2) local inflow from areas adjacent to the main streams which were correlated with flow in adjacent tributaries; and (3) local inflow from the river basin alluvium which was expressed as a constant rate per mile of river channel.
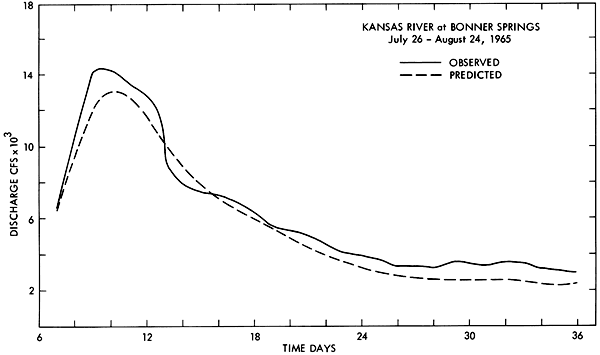
The model was tested for hydrologic verification by comparison of the observed versus predicted flows at selected gages on the main-stream rivers for eight time periods, each 36 days in length. The records selected are given in Table 4. All are periods before the development of significant reservoir regulation of the river network. A wide variation in relative discharge, antecedent soil moisture conditions, and storm patterns was observed during the time periods included in the test sample. Typical hydrograph comparisons obtained in these studies are given for the Smoky Hill River at Enterprise and the Kansas River at Bonner Springs in Figures 3 through 6. The hydrographs also illustrate several limitations of the model. These include the tendency to underestimate recession flow following a major discharge peak. This discrepancy is due to the omission of a bank storage mechanism in the program. Trouble is also experienced in reconstituting small, short-duration discharge peaks during extreme low-flow periods. These peaks are due to isolated thunderstorms which are occasionally missed by the model because of inadequate areal coverage in the discharge input points located in the western portion of the sub-basin. The significance of these peaks on downstream hydrographs in the Kansas River is very minor.
Table 4--United States Geological Survey stream-flow records used to test hydrologic verification of the lower Kansas River Basin model.
| February 15-March 22, 1961 |
| March 23-April 27, 1961 |
| August 26-September 30, 1961 |
| March 1-April 5, 1962 |
| November 1-December 6, 1962 |
| June 19-July 24, 1963 |
| June 1-July 6, 1964 |
| July 20-August 24, 1965 |
Figure 3--Observed and predicted discharge hydrographs for the period March 7, 1962, through April 5, 1962, for the Smoky Hill River at Enterprise.
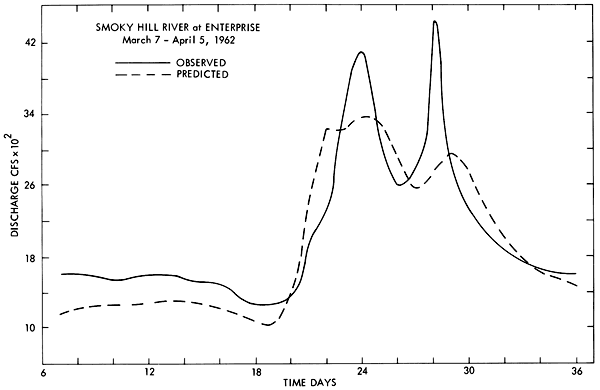
Figure 4--Observed and predicted discharge hydrographs for the period July 26, 1965, through August 24, 1965, for the Smoky Hill River at Enterprise.
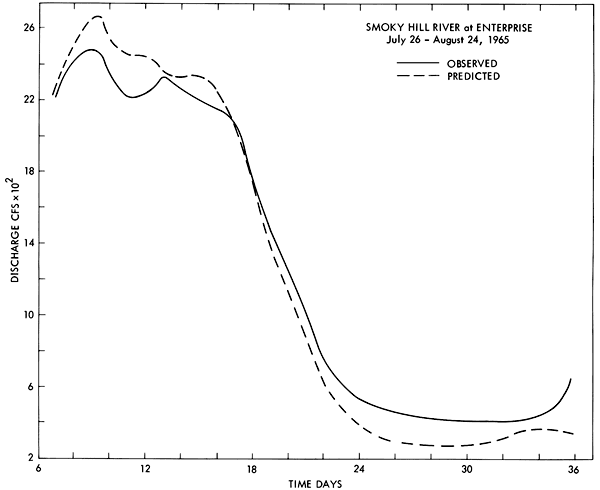
Figure 5--Observed and predicted discharge hydrographs for the period March 7, 1962, through April 5, 1962, for the Kansas River at Bonner Springs.
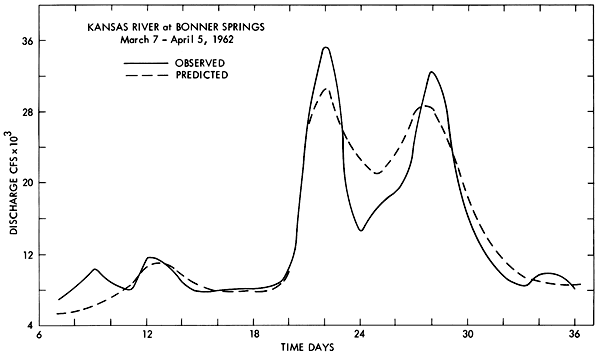
Figure 6--Observed and predicted discharge hydrographs for the period July 26, 1965, through August 24, 1965, for the Kansas River at Bonner Springs.
Discharge reconstitution in the upstream reaches of the model area is also affected by the sensitivity of the time scale for flow as the size of the drainage basin decreases. Verification could be improved for these areas by using climatic parameters, primarily precipitation and temperature, to generate individual tributary hydrographs (Smith and Lumb, 1966). This refinement does not appear justified for the present model in light of the field data currently available.
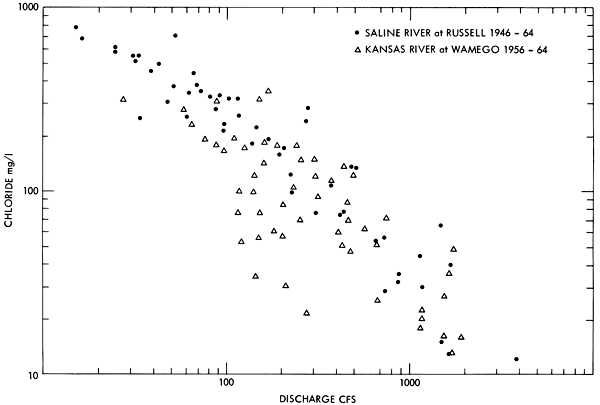
The conservative water quality in the river network at any point in the model is composed of the sum of the inorganic loads introduced into the system at the upstream reservoirs and the inorganic load related to any increase in discharge which occurs downstream of these reservoirs. Previous investigators have developed prediction equations for the concentration of individual ions as a function of discharge when the upstream drainage basin is relatively simple (Durum, 1953). A unique relationship between discharge and inorganic ion concentrations does not exist within the rivers included in the present model, however, because the total flow at any point in the river network may be composed of variable proportions of water from upstream reservoirs and the drainage areas below these impoundments. A distinct range of ion concentrations is thus hydrologically possible for each observed discharge. This phenomenon is illustrated in Figure 7 using data from the United States Geological Survey Water Quality Sampling Program. In this illustration a distinct relationship between chloride concentration and discharge is apparent for the Saline River at Russell. The Saline River above this site is a single, well-defined stream flowing through a basin of reasonably uniform geology. However, this distinct relationship completely vanishes for the Kansas River downstream at Wamego. In this instance there are five upstream tributaries, each having a distinctly different water quality, making up the total flow observed in the river. The ion concentration observed at any one point in time is thus dependent on the proportion of the total inflow from each tributary.
Figure 7--Observed variation of the concentration of chloride ion as a function of discharge for the Saline River near Russell, Kansas, and the Kansas River at Wamego, Kansas.
This range in ion concentration can be simulated in the model by separating each source of inorganic load and individually accounting for its distribution in the total river system. The load introduced at each of the reservoirs may be predicted by assuming that these bodies of water act as integrators of the dissolved solids entering the reservoirs. This integration is accomplished by mixing all of the incoming flow to produce a relatively narrow range of concentration for the dissolved solids in the water leaving the dam spillways (O'Brien and Angino, 1968).
The load introduced by discharge increases within the model area may be predicted by developing relationships between these increases in flow and the corresponding increase in load from a particular geologic area.
In the present model the 12 sampling stations operated by the United State Geological Survey (Fig. 2) provided data for analysis. Grab samples collected from these stations prior to construction of any of the reservoirs except Kanopolis were used to develop relationships between discharge and load increases in the system.
While regression equations between ion concentration and discharge were not in themselves useful for the prediction of water quality because of the tributary mixing effect previously discussed, these equations were useful in developing relationships between increases in discharge and increases in load. The regression equations considered are summarized in Table 5. The hyperbolic relationship, equation (2), and the exponential relationship, equation (3), consistently exhibited correlation coefficients between 0.6 and 0.7 and were adopted for use. Sampling stations located in the Cretaceous and Pennsylvanian subregions were best characterized by a hyperbolic relationship. Waters arising in or passing through the Permian subregion were best defined by exponential equations. Exceptions to these generalizations were the Saline River at Tescott where the Dakota Formation greatly influences the dissolved-solids concentration at low flows, and the stations located on the lower Kansas River which are predominantly influenced by the water originating in the Permian region upstream. In both of these instances the relationship between the discharge and a specific ion were best described by exponential equations.
Table 5--Equations tested to define a relationship between specific ion concentration and discharge.
| Equation number |
Equation form |
|---|---|
| (1) | I = A + BQ |
| (2) | I = CQD |
| (3) | I = 10(E-FQ) |
| (4) | I = G + H (log Q) |
| (5) | I = K + 4Q |
| (6) | I = M + NQ + OQ2 . . . PQ5 |
| Where I = specific ion concentration, mg/l, Q = discharge, CFS A, B ... P = coefficients, constants, or exponents |
|
The equations relating discharge and specific ion concentration at each station were used in conjunction with mean monthly discharge correlations between stations to develop a relationship between the increase in discharge and the increase in the load of a particular ion between the stations. An example of the procedure followed is presented in Figures 8 through 11 for the chloride ion originating in the drainage area between Beloit and Niles on the Solomon River.
The regression equations between chloride concentration and discharge shown in Figure 8 and Figure 9 were converted to a relationship between chloride load in tons per day and discharge by the equation:
Load = 0.0027 QC
where
Load = tons/day of the ion species
0.0027 = conversion factor
Q = discharge, CFS
C = concentration of the ion species in mg/l at discharge Q
The relationship produced in this manner is indicated by the dashed line in each figure.
Figure 8--The concentration and load of chloride ion as a function of discharge for the Solomon River at Beloit.
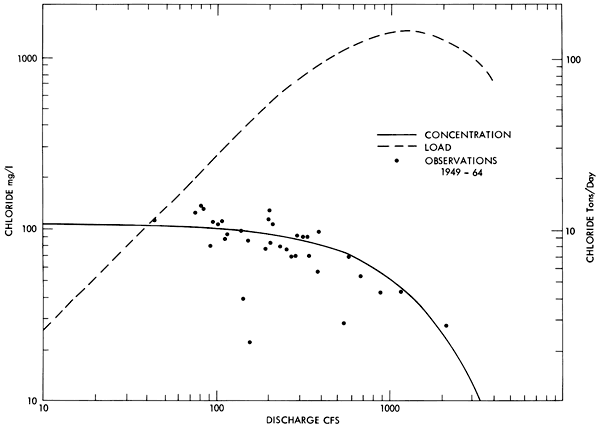
Figure 9--The concentration and load of chloride ion as a function of discharge for the Solomon River at Niles.
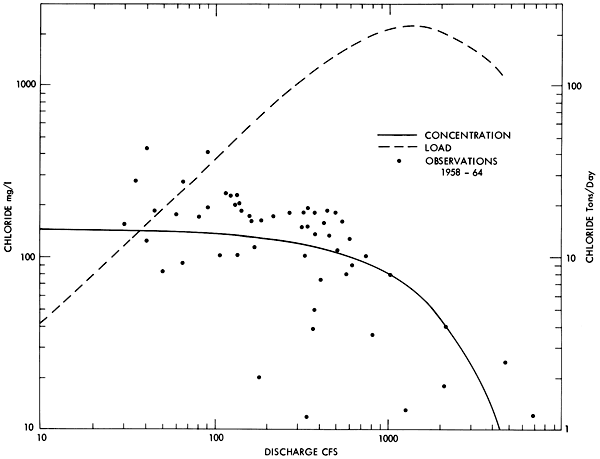
The apparent decrease in chloride load at high discharge shown in Figures 8 and 9 was reproduced many times within the model area and possibly indicated a reversal in the movement of ground water during high river stages. A similar mechanism has been suggested for localized brine-control measures in the Arkansas and Red River basins in southern Kansas and Oklahoma (DeGeer and Ball, 1968).
The discharge correlation between stations (Fig. 10) was used as a basis for subtraction between the two load curves to produce an equation, indicated by line A on Figure 11, which relates the increase in discharge between these stations to the increase in chloride load.
Figure 10--Mean monthly discharge correlation between the Solomon River at Beloit and the Solomon River at Niles.
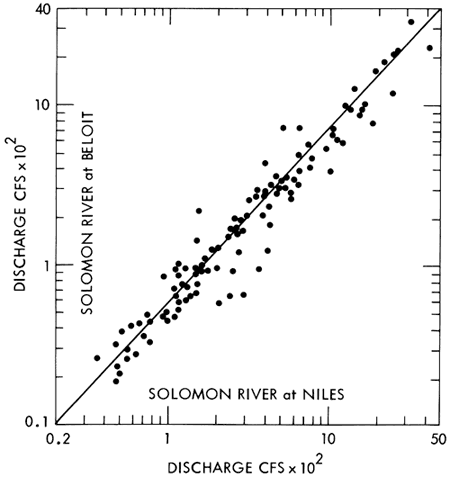
Figure 11--The change in chloride load added between Beloit and Niles on the Solomon River as a function of the increase in discharge between these locations.
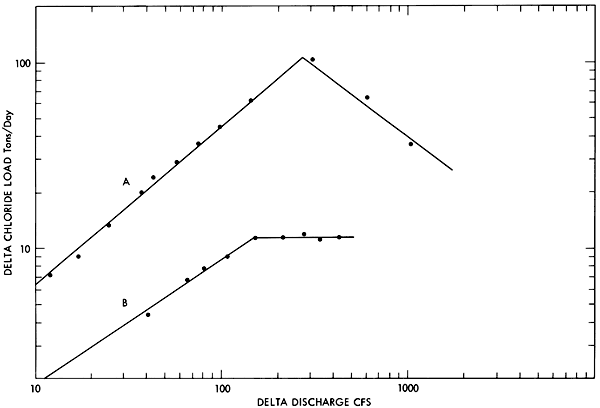
Any combination of adjacent stations can be correlated in this manner to produce an equation relating the increase in discharge and the increase in load. For instance, Line B on Figure 11 is applicable below Enterprise on the Smoky Hill River and above Wamego on the Kansas River.
The total number of water quality sub-areas created in this way for the present model are outlined in Figure 12 along with the approximate boundaries of the geological regions previously described. The magnitude of the equations illustrated in Figure 11 are what would be expected on the basis of the general characteristics of each geologic subdivision. There is no chloride added in area C which is in the Pennsylvanian System.
Figure 12--Conservative water quality sub-areas in current use in the lower Kansas River Basin model.
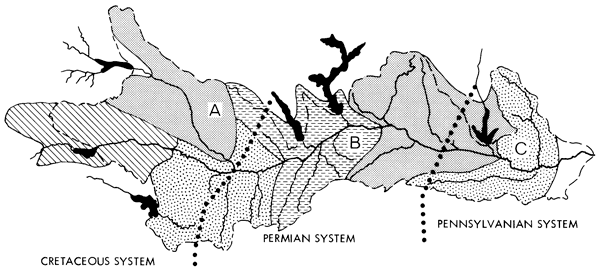
The shape of the subdivision in Figure 12 also shows the approximations made between the areal applicability of the water quality sub-area and the hydrologic boundaries of the model area. These approximations were dictated by the available field observations.
Any number of individual ions can be included by the technique previously outlined. At the current time, conservative vectors for chloride, sulfate, calcium and magnesium have been developed.
Scatter diagrams comparing the predicted and observed concentrations for each ion at each water quality station were obtained for each time interval included in Table 4. Typical results for both chloride and sulfate are presented in Figures 13 through 16 for the Smoky Hill River at Enterprise and the Kansas River at Bonner Springs. The similarity between the predicted and the observed range of concentration for each of these stations indicates the model appears to be generating and routing the individual ion species through the basin in a necessarily simplified but nevertheless analogous manner to what occurs in nature.
Figure 13--Observed and predicted chloride ion concentration as a function of discharge for the Smoky Hill at Enterprise. [Note: symbols are labeled differently on this plot than on 14, 15, and 16, and may be in error.]
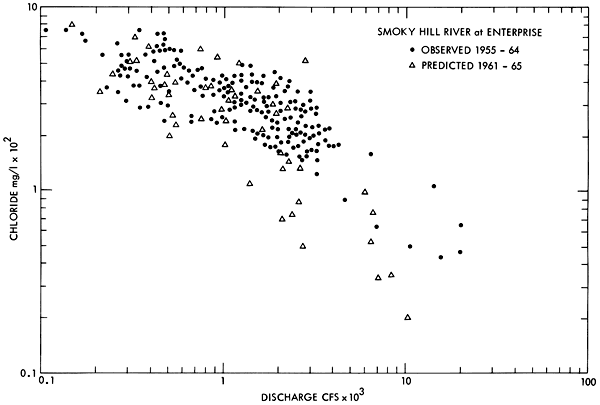
Figure 14--Observed and predicted sulfate ion concentration as a function of discharge for the Smoky Hill River at Enterprise.
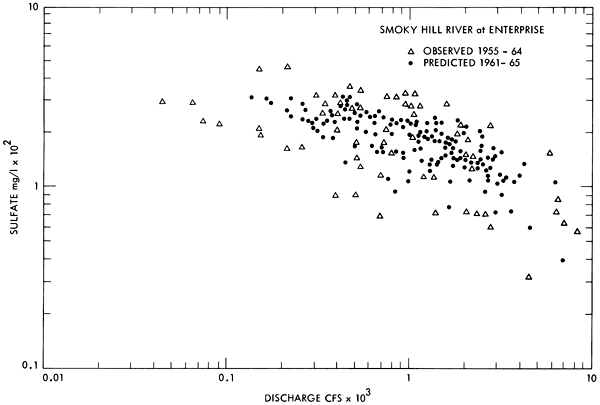
Figure 15--Observed and predicted chloride ion concentration as a function of discharge for the Kansas River at Bonner Springs.
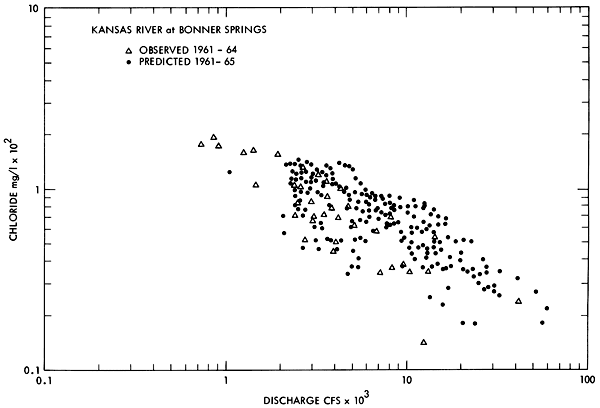
Figure 16--Observed and predicted sulfate ion concentration as a function of discharge for the Kansas River at Bonner Springs.
A more stringent test of this hypothesis can be made by comparing individual observed values of the various ions to the values predicted by the model for the same date. A compilation of results obtained by this analysis is given in Table 6.
Table 6--Comparison of observed and predicted ion concentration for historical discharge periods in the lower Kansas River Basin.
| Sampling station and date |
Discharge (CFS) |
Sulfate (mg/l) |
Chloride (mg/l) |
Calcium (mg/l) |
Magnesium (mg/l) |
|||||
|---|---|---|---|---|---|---|---|---|---|---|
| Obs. | Pred. | Obs. | Pred. | Obs. | Pred. | Obs. | Pred. | Obs. | Pred. | |
| Bonner Springs | ||||||||||
| 3/14/1962 | 8,460 | 9,227 | 97 | 68 | 70 | 61 | 90 | 71 | 17 | 14 |
| Lecompton | ||||||||||
| 3/29/1962 | 20,000 | 20,303 | 53 | 33 | 24 | 36 | 52 | 34 | 10 | 6 |
| 6/28/1963 | 2,410 | 2,258 | 82 | 117 | 75 | 126 | 66 | 83 | 15 | 8 |
| Wamego | ||||||||||
| 4/04/1962 | 6,660 | 6,130 | 88 | 89 | 50 | 102 | 67 | 77 | 17 | 15 |
| 7/01/1963 | 11,600 | 11,160 | 48 | 45 | 22 | 51 | 55 | 48 | 16 | 8 |
| Enterprise | ||||||||||
| 4/04/1962 | 1,640 | 1,545 | 216 | 117 | 282 | 262 | 158 | 106 | 27 | 21 |
| 7/01/1963 | 552 | 675 | 146 | 110 | 288 | 241 | 80 | 59 | 16 | 17 |
| Tescott | ||||||||||
| 3/13/1962 | 249 | 255 | 398 | 154 | 490 | 196 | 174 | 100 | 32 | 17 |
| 7/03/1963 | 65 | 63 | 258 | 248 | 380 | 289 | 105 | 124 | 28 | 28 |
The observed data in this table were obtained from grab samples taken at various times during the day. The predicted values are computed on the basis of average daily discharges. This difference must be considered when evaluating the significance of the comparisons given in the table because the hydrographs immediately preceding and following the day of the field observation must be considered. If the discharge is either increasing or decreasing rapidly, the field sample may not be representative of the average daily concentration. This factor is present to an unknown degree in the observations at Bonner Springs on March 14, 1962; Lecompton on March 29, 1962; Wamego on April 4, 1962; and Enterprise on July 1, 1963.
Differences between the predicted and the observed data also occur because the water quality entering the model at each of the reservoir sites was assumed to be defined by a specific line of regression based on the naturally occurring water quality at that location. As illustrated by Figure 8, which corresponds to the reservoir input for the Solomon River prior to the construction of Glen Elder Reservoir, this assumption is often erroneous. The magnitude of this boundary error will decrease when the reservoirs are in operation and the water quality from these sources is more nearly uniform.
The differences between the observed and predicted values for chloride are not unexpected in light of the relatively concentrated sources of chloride associated with the Dakota Formation. As indicated in Figure 12, the conservative vector for a particular region represents average conditions over a relatively large area. While this is adequate when the source of the ion is relatively diffuse, such as is the case for calcium and sulfate, it cannot adequately account for highly variable contributions from naturally occurring point sources.
The agreement between observed and predicted concentrations of dissolved solids could also be improved by separately identifying the ground-water contributions in the model. However, the data necessary for developing these relationships are not available at the present time.
The basic task of a mathematical model of any river basin is to perform a continuous mass balance on the water and the conservative pollutant in the system and to route both of these substances through the river network in a way which closely approximates the actual prototype.
The present model is an attempt to do this through the use of a program having the flow diagram illustrated in Figure 17. The program is quite general with extensive use of logical IF statements for the detailed computational effort. This will facilitate model modification as more information becomes available on the interactions between quality parameters and will facilitate adaptation of the program to other midwestern river basins. Definition of model parameters and a program listing are available as an open-file report from the Kansas Geological Survey.
Figure 17--Flow diagram of the computer program for the dynamic conservative model.
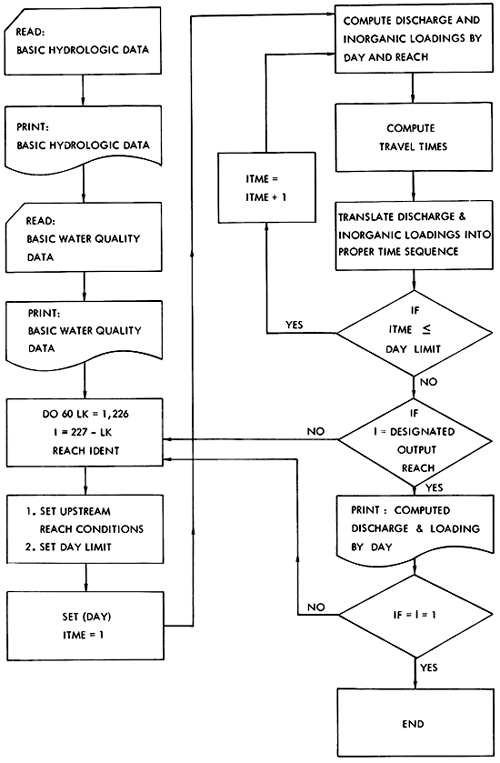
The mathematical model described in this paper is representative of the level of sophistication which can be obtained in water quality simulation on large midwestern river basins with the field observations routinely available.
This model is deterministic because the reservoirs surrounding the study area were designed as multipurpose projects prior to the development of the model. However, it would be feasible to use stochastic inputs for the 14 tributary input gages downstream of the reservoirs (Quimpo, 1968).
Possible applications of the model include: evaluation of the effect of proposed reservoir operating policies on downstream water quality; determination of the effect of proposed irrigation developments upstream of the reservoirs on the quantity and quality of the flow in the downstream river network; and evaluation of the impact of potential industrial developments at various locations in the basin.
Degeer, M. W., and Ball, J. C., 1968, Chloride control--Arkansas and Red River Basins: Jour. Sanitary Engr. Div., Am. Soc. Civil Engr., v. 94, no. SA1, Proc. Paper 5812.
Durum, W. H., 1953, Relationship of the mineral constituents in solution to stream flow, Saline River near Russell, Kansas: Trans. Am. Geophys. Union, v. 34, p. 435.
Furness, L. W., 1959, Kansas stream-flow characteristics, Part I Flow Duration: Kansas Water Resources Board, Tech. Rept. No. 1, Topeka, Kansas.
Kansas State Department of Health, 1967, Water quality and time of travel investigations in the lower Kansas River Basin: Final Report, Project WA66-3, Topeka, Kansas.
Leopold, L. B., and Maddock, T., Jr., 1953, The hydraulic geometry of stream channels and some physiographic implications: U. S. Geol. Survey, Prof. Paper 252. [available online]
O'Brien, W. J., and Angino, E. E., 1968, Further investigation into the water quality parameters used in the lower Kansas River Basin model, Report 1: Univ. Kansas, Center for Research, Inc., Engr. Sci. Div. (Contract 14-14-58), Lawrence, Kansas.
Quimpo, R. G., 1968, Stochastic analysis of daily river flows: Jour. Hydraul. Div., Am. Soc. Civil Engr., v. 94, no. HY1, Proc. Paper 5719.
Smith, R. L., and Lumb, A. M., 1966, Derivation of basin hydrographs: Kansas Water Resour. Res. Inst., Contrib. No. 19, Manhattan, Kansas.
Smith, R. L., O'Brien, W. J., LeFeuvre, A. R., and Pogge, E. C., 1966, Development and evaluation of a mathematical model of the lower reaches of the Kansas River drainage system, Report 11: Univ. Kansas, Center for Research, Inc., Engr. Sci. Div. (Project PH 86-66-63), Lawrence, Kansas.
U.S. Corps of Engineers, 1967, Investigation of water quality, Tuttle Creek Reservoir, 1963 through June 1966: Department of the Army, Kansas City District, Kansas City, Missouri.
Kansas Geological Survey, Geology
Placed on web Nov. 4, 2008; originally published in Aug. 1972.
Comments to webadmin@kgs.ku.edu
The URL for this page is http://www.kgs.ku.edu/Publications/Bulletins/204_3/index.html