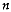 comprising
comprising
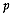 attributes, is there any
evidence for clustering the sites into groups
scattered around centroids, as against the alternative hypothesis that
they are an unstructured coregionalization?
attributes, is there any
evidence for clustering the sites into groups
scattered around centroids, as against the alternative hypothesis that
they are an unstructured coregionalization?
Hodgeman County Study, part 3 of 12
In classical applications of discriminant analysis, one employs a training set including direct indicators of group membership. Medical science provides good examples. In certain instances, a group of sick patients is carefully examined to prepare a clinical record relating internal conditions to their external symptoms and laboratory analyses, a costly and lengthy classification only possible after performing surgery or autopsy. In this context, based only on external symptoms and laboratory analyses, the task of discriminant analysis is to determine the probability that other patients suffer the internal conditions considered in the training set.
In earth sciences what prevails is the equivalent of knowing only
the external symptoms and never knowing the group assignments. Even
worse, the nature and number of the groups is seldom known.
Determining the groups is as important in such studies as the
assignments themselves. In such a situation one replaces the
training set assignments by a typification using another method
able to decide both the number and characteristics of the groups.
The best alternative is cluster analysis, which aside from any prior
information not contained in the data, solves the following problem:
given a coregionalization sampling of size
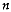 comprising
comprising
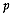 attributes, is there any
evidence for clustering the sites into groups
scattered around centroids, as against the alternative hypothesis that
they are an unstructured coregionalization?
attributes, is there any
evidence for clustering the sites into groups
scattered around centroids, as against the alternative hypothesis that
they are an unstructured coregionalization?
There are several ways to define and find the clusters depending
partly on the metric used to determine proximity among the sites in
the 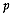 dimensional
attribute space, the Euclidean distance being
the most common and the only one considered here. The geographical
distance is completely ignored both in cluster analysis and in
discriminant analysis and is only considered at the final mapping
stage of regionalized classification.
dimensional
attribute space, the Euclidean distance being
the most common and the only one considered here. The geographical
distance is completely ignored both in cluster analysis and in
discriminant analysis and is only considered at the final mapping
stage of regionalized classification.
There have been many studies comparing various methods of cluster analysis using artificial data sets containing known clusters produced by Monte Carlo methods. In most of these studies the Ward's minimum variance method has been the one with the best overall performance on reproducing the known clusters (SAS, 1990, p. 56).
Previous Page--Introduction ||
Next Page--Ward's Method
Dakota Home ||
Start of Hodgeman County Study