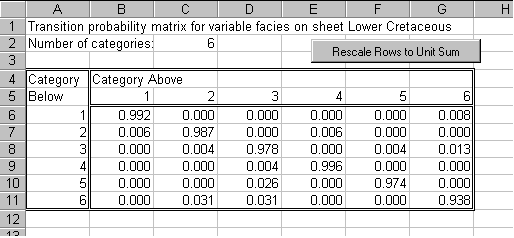

In many geological applications, the sequence of categories may be meaningful. For example, the categorical variable may represent facies, in which case one would expect to see transitions between facies representing physically adjacent depositional environments more often than transitions between more widely separated environments. The relative number of transitions between each possible pair of categories can be used to compute a transition probability matrix, such as that employed in Markov analysis of facies sequences (Doveton, 1994). Kipling contains code to compute a transition probability matrix from an observed sequence of categorical values. The transition probablities can then be used to modify the facies membership probabilities based on logs (or other predictors) alone, resulting in a predicted facies sequence that more closely reflects expected patterns of facies thickness and adjacency.
We will illustrate the incorporation of transition probability information into the prediction of facies for the Jones #1 well described in the categorical prediction example. The worksheet below contains the transition probability matrix computed by Kipling from the sequence of core-based facies designations for Jones #1. The entries in the transition probablity matrix are given by the number of observed transitions from each facies (row) upward to every other facies (column), scaled to a unit-sum across rows to yield probabilities:

We then use the transition probability matrix to modify the set of facies membership probabilities computed from the logs alone, yielding the probabilities and predicted facies shown below. The modified sequence of predicted facies for the Jones #1 well is considerably less erratic and looks much more like the sequence of assigned facies from core:
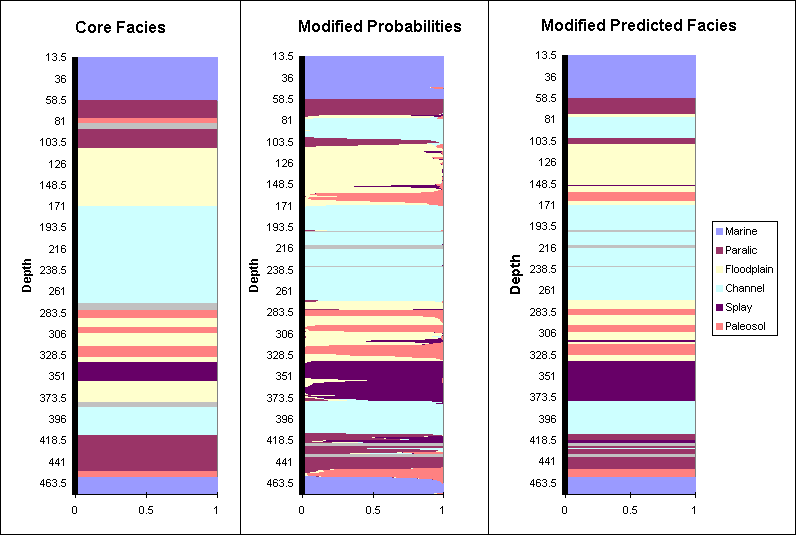
The computed transition probability matrix reflects the characteristics of the particular sequence of observed facies employed in the computation. These particular characteristics may diverge somewhat from the expected sequence characteristics for a region. For example, a transition from facies A to facies B may never occur in the selected core, although it is known to occur elsewhere in the study area. To overcome this shortcoming, Kipling allows the user to modify the computed TPM to better match geological expectations. This is accomplished simply by editing the entries in the matrix. Because the modified facies membership probabilities are linked by formulas to the transition probability matrix, any changes to this matrix will automatically be reflected in the modified probabilities and facies predictions, and also in any existing plots of those values. This allows you to easily investigate the influence of the transition probability values on the sequence of predicted facies.
Previous Page--Categorical Example ||
Kipling Home || Next
Page--References