|
||||||||||
Attributes
Multi-trace Seismic Attributes
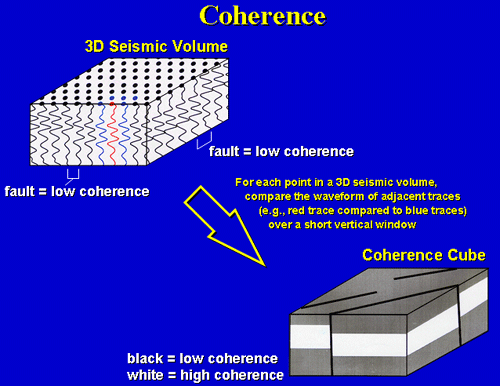
Seismic Coherence
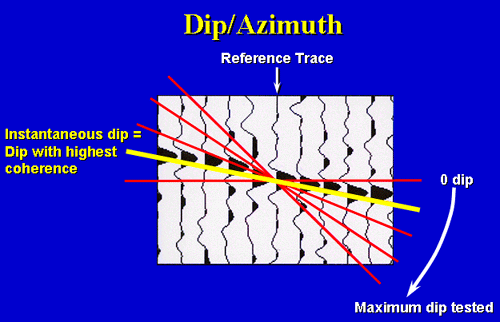
Dip/Azimuth
A schematic 2-D representation of the dip/azimuth calculation. Coherence is calculated for a range of dips (red lines), and in 3-D, azimuths, within a small analysis window around a reference trace. The dip/azimuth combination which has the highest coherence is assigned to be the instantaneous dip/azimuth for the point at the center of the analysis window. CurvatureCurvature describes how bent a surface is at a particular point and is closely related to the second derivative of the curve defining the surface. The more bent a surface is, the larger its curvature.
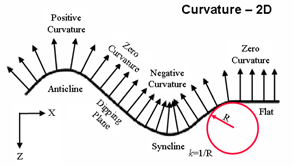
In two dimensions, positive curvature refers to an antiform feature, negative curvature refers to a synform feature, and zero curvature refers to a planar feature.
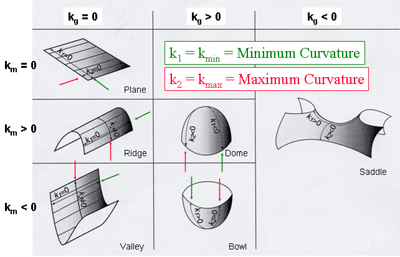
In three dimensions, curvature may be computed at any azimuth about a point, but the most useful curvatures are those defined by planes that are orthogonal to the surface, referred to as normal curvatures. The principal curvatures (maximum curvature and minimum curvature) are one set of normal curvatures.
Maximum Curvature (kmax) - measure of the maximum bending (positive or negative) of the surface at a point
These curvatures can be combined to define other curvature attributes, such as:
Other important curvatures include: Most Positive Curvature – most positive value obtained from a search of all possible normal curvatures at a point
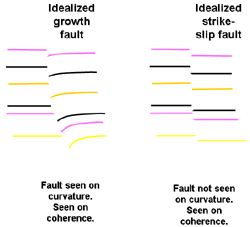
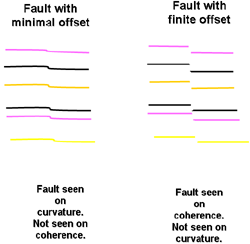
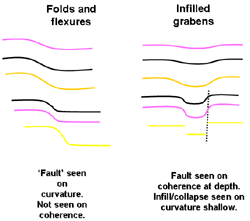
Various curvature attributes have been shown to reveal useful information relating to folds, faults, and lineaments contained within the surface (Roberts, 2001).
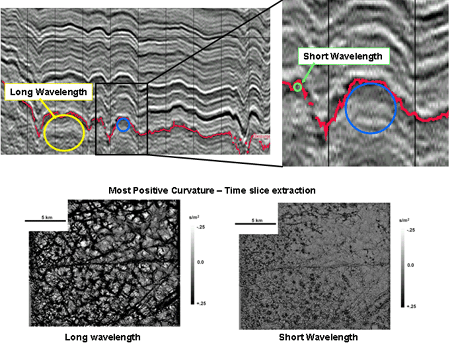
Curvature and rotation are fractal in nature and amenable to multispectral analysis. Long wavelength curvature shows broader features. Short wavelength shows additional detail.
Previous workers (e.g., Lisle, 1994; Roberts, 2001) have computed curvature of surfaces interpreted directly from 3-D seismic data whose inline and crossline format create a natural grid. This method suffers from seismic noise and other interpretation problems and treats only a single, well-imaged horizon. Al-Dossary and Marfurt (2005) describe a method of using a moving subvolume to compute curvatures at every point within a 3-D seismic volume. This eliminates interpretation problems and allows us to slice the curvature volumes along time (pseudo depth) or to extract along horizons, thereby allowing us to better image irregular karst features.
Our method
|
||||||||||