





Dakota Aquifer Program--Geologic Framework
Hodgeman County Study, part 6 of 12
Allocation by Extension
The use that regionalized classification makes of discriminant
analysis is to a certain degree analogous to the use of
crossvalidation in kriging and different from the classical
use of discriminant analysis. Classical use of discriminant
analysis employs the training set for calibration and then
proceeds to classify vectorial measurements without assigments.
In regionalized classification the interest is in the calculation
of the probabilities 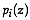 for the
same realizations in the training set already classified by the
prior cluster analysis. Once one has all the probabilities
for the
same realizations in the training set already classified by the
prior cluster analysis. Once one has all the probabilities
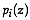 , reallocation of the sites
to the group with the highest probability is a trivial endeavor.
This reallocation offers an opportunity to check results and compare
methods in case the user wants to consider more than one type of
cluster analysis or discriminant analysis. Results from cluster
and discriminant analysis should be comparable only with minor
variations that one should employ to select methods and
parameters yielding the most consistent results.
, reallocation of the sites
to the group with the highest probability is a trivial endeavor.
This reallocation offers an opportunity to check results and compare
methods in case the user wants to consider more than one type of
cluster analysis or discriminant analysis. Results from cluster
and discriminant analysis should be comparable only with minor
variations that one should employ to select methods and
parameters yielding the most consistent results.
The final step in regionalized classification is the mapping
of groups, which one can accomplish by arbitrarily assigning
colors or black and white patterns to the groups. As arbitrary
as the color or pattern selection may be, it always helps to
select a combination of alternatives that maximizes contrast to
the eye, which customarily requires some experimentation by trial
and error.
Most mapping procedures require a collection of values regularly
spaced at short intervals, which is rarely the case of training
sets. In addition, interpolation presumes that the variable is
continuous. In those circumstances Harff and Davis (1990)
recommend mapping the group probabilities
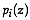 by treating them as
regionalized variables and then use the allocation rule to
produce the discontinuous group map. Remember that
by treating them as
regionalized variables and then use the allocation rule to
produce the discontinuous group map. Remember that
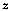 is a shorthand for
is a shorthand for
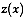 , where
, where
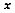 is the location of the site.
Then the probabilities are actually regionalized variables
is the location of the site.
Then the probabilities are actually regionalized variables
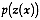 or
or
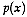 that depend on location.
One does group allocation node by node performing a grid-to-grid
operation in which one assigns each node to the group with the
highest probability.
that depend on location.
One does group allocation node by node performing a grid-to-grid
operation in which one assigns each node to the group with the
highest probability.
Considering that each site must be fully sampled to allow for
the cluster and discriminant analysis, there is no advantage on
using cokriging for the estimations. Although the probabilities
sum to a constant, use of alr transformation is not feasible due
to the numerous zeros both in the numerator resulting in a null
argument for the logarithm, or in the denominator producing
unacceptable ratios.
Ordinary or universal kriging, the default geostatistical options
of choice, suffer from the inability to restrict the estimates to
an interval—0-1 in this instance—let alone to force the probabilities
to sum to one. Estimates outside the 0-1 interval, however, are
rare and never far away from the interval. A common solution to
force a vector in a coregionalization to add to one is to rescale
the values. Considering that such correction does not change the
ranking of the membership probabilities, the allocation is
insensitive to the rescaling.
Alternative strategies involving the interpolation of the
coregionalization itself or of the generalized distances instead
of the membership probabilities are deceptive choices. Although
the probabilities end up honoring all constraints, the use of
estimates instead of true values results in unaccounted propagation
of errors.
Allocation in regionalized classification remains open to improvements.
Algorithm 3
This is a procedure for the regionalized classification of fully
sampled coregionalizations involving 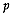 attributes.
attributes.
- Assign the sites to one and only one of
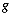 groups either by using Algorithm
1 or any other cluster analysis procedure, or on the basis of
external information
groups either by using Algorithm
1 or any other cluster analysis procedure, or on the basis of
external information
- For each site calculate the group probabilities either by Algorithm 2 or any other discriminant analysis procedure deemed appropriate.
- If the mapping procedure does not require a regular grid of values, go to step 4. Otherwise, use some form of kriging to produce grids of estimated values for every group probability.
- For every site or node, assign the site or node to the group with the largest probability.
- Prepare a map showing the group assignment. This is the regionalized classification of the area under study, conditional to the values and attributes in the sampling.
- Prepare a map of the highest probability per node. This is the probability that the site in the regionalized classification indeed belongs to the group in the regionalized classification.
- Prepare a censored map eliminating nodes or sites likely to be misclassified, which are more likely to occur when the highest probability is only marginally larger than the second highest probability.
Previous Page--Discriminant Analysis ||
Next Page--The Dakota Aquifer Program Study
Dakota Home ||
Start of Hodgeman County Study
Kansas Geological Survey, Dakota Aquifer Program
Updated Sept. 16, 1996.
Scientific comments to P. Allen Macfarlane
Web comments to webadmin@kgs.ku.edu
The URL for this page is HTTP://www.kgs.ku.edu/Dakota/vol1/geo/hodge6.htm
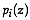 for the
same realizations in the training set already classified by the
prior cluster analysis. Once one has all the probabilities
for the
same realizations in the training set already classified by the
prior cluster analysis. Once one has all the probabilities
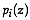 , reallocation of the sites
to the group with the highest probability is a trivial endeavor.
This reallocation offers an opportunity to check results and compare
methods in case the user wants to consider more than one type of
cluster analysis or discriminant analysis. Results from cluster
and discriminant analysis should be comparable only with minor
variations that one should employ to select methods and
parameters yielding the most consistent results.
, reallocation of the sites
to the group with the highest probability is a trivial endeavor.
This reallocation offers an opportunity to check results and compare
methods in case the user wants to consider more than one type of
cluster analysis or discriminant analysis. Results from cluster
and discriminant analysis should be comparable only with minor
variations that one should employ to select methods and
parameters yielding the most consistent results.
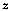 is a shorthand for
is a shorthand for
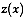 , where
, where
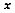 is the location of the site.
Then the probabilities are actually regionalized variables
is the location of the site.
Then the probabilities are actually regionalized variables
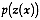 or
or
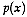 that depend on location.
One does group allocation node by node performing a grid-to-grid
operation in which one assigns each node to the group with the
highest probability.
that depend on location.
One does group allocation node by node performing a grid-to-grid
operation in which one assigns each node to the group with the
highest probability.
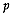 attributes.
attributes.
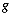 groups either by using Algorithm
1 or any other cluster analysis procedure, or on the basis of
external information
groups either by using Algorithm
1 or any other cluster analysis procedure, or on the basis of
external information