Hodgeman County Study, part 4 of 12
 sites, this heuristic method progresses by reducing
the number of clusters one at a time starting from the trivial extreme
case of one cluster per site and ending at the other trivial extreme
case in which one cluster comprises all the sites. At each cluster
reduction, the method merges the two clusters resulting in the
smallest increase in the total sum of squares of the distances of each
point to its cluster centroid. Sites clustered at a previous
clustering step are never unmerged.
sites, this heuristic method progresses by reducing
the number of clusters one at a time starting from the trivial extreme
case of one cluster per site and ending at the other trivial extreme
case in which one cluster comprises all the sites. At each cluster
reduction, the method merges the two clusters resulting in the
smallest increase in the total sum of squares of the distances of each
point to its cluster centroid. Sites clustered at a previous
clustering step are never unmerged.
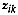 be vector of attribute values
at site
be vector of attribute values
at site 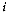 assigned to cluster
assigned to cluster 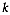 whose size is
whose size is
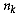 and mean is
and mean is
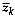 . Then the error sum of
squares for cluster
. Then the error sum of
squares for cluster 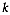 is
is
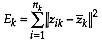
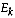 be the error sum of squares
in Definition 1 and let
be the error sum of squares
in Definition 1 and let 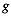 be the total number of clusters.
The total within group error sum of squares is
be the total number of clusters.
The total within group error sum of squares is
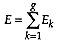
Table 1 and Figure 2 illustrate the method for a simple case involving
a single attribute. At the beginning each measurement coincides with
its centroid and both the error per cluster and consequently the total
error are zero. In the first round of mergers, only the merging sites
contribute to the total sum, so 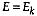 .
.
For large numbers of clusters, instead of computing the new total sum
of errors directly as the sum of all clusters in Definition 2, there
are savings in the calculations by computing the new total sum of
errors as the lowest sum from the previous round, plus the new error
for the new merging clusters, minus the individual cluster errors for
the merging clusters. Even larger savings arise by working directly
with the square distances between centroids instead of the within
square distances 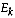 (Anderberg, 1973,
p. 142-145; Kendall, 1986, p. 37).
(Anderberg, 1973,
p. 142-145; Kendall, 1986, p. 37).
Table 1. Example illustrating the application of the Ward's method showing the error sum of squares and the total within group error sum of squares only for the bold, new partitions plus the mean for the best mergers.
| Number of clusters | Possible partitions of the measurements | 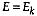 | 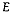 | 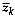 |
6 | (0.1) (1) (3) (7) (8) (10) | 5 | (0.1, 1) (3) (7) (8) (10) | 0.405 | 0.405 | 0.55 | (0.1, 3) (1) (7) (8) (10) | 4.205 | 4.205 | (0.1, 7) (1) (3) (8) (10) | 23.805 | 23.805 | (0.1, 8) (1) (3) (7) (10) | 31.205 | 31.205 | (0.1, 10) (1) (3) (7) (8) | 49.005 | 49.005 | (0.1) (1, 3) (7) (8) (10) | 2 | 2 | (0.1) (1, 7) (3) (8) (10) | 1 | 18 | (0.1) (1, 8) (3) (7) (10) | 24.5 | 24.5 | (0.1) (1, 10) (3) (7) (8) | 40.5 | 40.5 | (0.1) (1) (3, 7) (8) (10) | 8 | 8 | (0.1) (1) (3, 8) (7) (10) | 12.5 | 12.5 | (0.1) (1) (3, 10) (7) (8) | 24.5 | 24.5 | (0.1) (1) (3) (7, 8) (10) | 0.5 | 0.5 | (0.1) (1) (3) (7, 10) (8) | 4.5 | 4.5 | (0.1) (1) (3) (7) (8, 10) | 2 | 2 | 4 | (0.1, 1, 3) (7) (8) (10) | 4.407 | 4.407 | (0.1, 1, 7) (3) (8) (10) | 28.14 | 28.14 | (0.1, 1, 8) (3) (7) (10) | 37.407 | 37.407 | (0.1, 1, 10) (3) (7) (8) | 59.94 | 59.94 | (0.1, 1) (3, 7) (8) (10) | 8 | 8.405 | (0.1, 1) (3, 8) (7) (10) | 12.5 | 12.905 | (0.1, 1) (3, 10) (7) (8) | 24.5 | 24.905 | (0.1, 1) (3) (7, 8) (10) | 0.5 | 0.905 | 7.5 | (0.1, 1) (3) (7, 10) (8) | 4.5 | 4.905 | (0.1, 1) (3) (7) (8, 10) | 2 | 2.405 | 3 | (0.1, 1, 3) (7, 8) (10) | 4.407 | 4.907 | 1.367 | (0.1, 1, 7, 8) (3) (10) | 49.208 | 49.208 | (0.1, 1, 10) (3) (7, 8) | 59.94 | 60.44 | (0.1, 1) (3, 7, 8) (10) | 14 | 14.405 | (0.1, 1) (3, 10) (7, 8) | 24.5 | 24.905 | (0.1, 1) (3) (7, 8, 10) | 4.667 | 5.077 | 2 | (0.1, 1, 3, 7, 8) (10) | 50.048 | 50.048 | (0.1, 1, 3 , 10) (7, 8) | 60.308 | 60.808 | (0.1, 1, 3) (7, 8, 10) | 4.667 | 9.074 | 8.333 | 1 | (0.1, 1, 3, 7, 8, 10) | 81.875 | 81.875 | 4.85 |
Figure 2. The Ward's method tree for the example in Table 1.
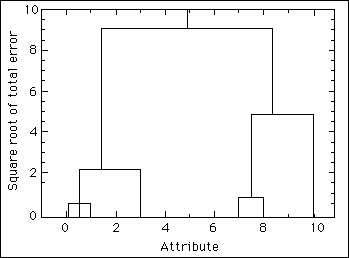
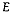 in Definition 2 is zero.
in Definition 2 is zero.
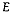 .
.
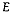 or total number of clusters
or total number of clusters 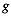 .
.
Most statistical packages include implementations of several methods for cluster analysis, including Ward's (IMSL, 1987; SAS Institute, 1990). Among the properties of Ward's method one has:
(a) The method is biased toward finding clusters with the same number of sites in each cluster (SAS, 1990, p. 56).
(b) Because sites clustered at a previous clustering step are
never unmerged, the calculations are relatively simple, but they
often result in suboptimal partitions conditioned to the previous
steps. For example, at the three cluster level the method produces
the clusters (1, 2), (4, 6), (9, 10) for this univariate sampling of
size 6. In the next stage the method produces the clusters
(1, 2, 4, 6) and (9, 10) with total error 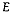 =15.25, which
is larger than the smallest total error
=15.25, which
is larger than the smallest total error 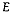 =13.333 associated
with clusters (1, 2, 4) and (6, 9, 10), an unfeasible partition
after selecting (1, 2), (4, 6), (9, 10) in the previous stage.
=13.333 associated
with clusters (1, 2, 4) and (6, 9, 10), an unfeasible partition
after selecting (1, 2), (4, 6), (9, 10) in the previous stage.
Despite its suboptimality, the method has been quite successful reproducing clusters in blind tests.
(c) Ward's method is unable to avoid calculations for the partitions involving small clusters when they are of no interest. For example for a sampling of size 1,000, if the interest is restricted to partitions with 5 to 20 clusters, it is possible to stop the calculations after completing the partition into 5 clusters, but it is not possible to avoid the more numerous calculations for partitioning the sampling from 999 to 21 clusters.
(d) The total sum of errors increases monotonically as the number of clusters decreases.
(e) The method is not robust with respect to survey errors and outliers (Mojena, 1988).
Previous Page--Typification ||
Next Page--Discriminant Analysis
Dakota Home ||
Start of Hodgeman County Study